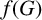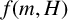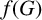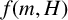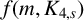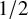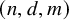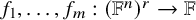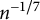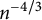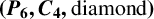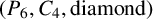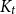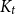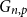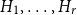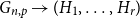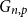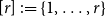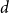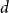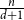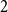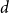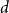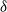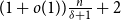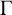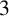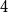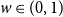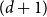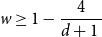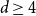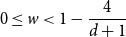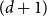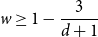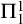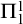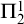Refine listing
Actions for selected content:
1007 results in 05Cxx
MAX-CUT BY EXCLUDING BIPARTITE SUBGRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 08 November 2022, pp. 177-186
- Print publication:
- October 2023
-
- Article
- Export citation
Ramsey properties of algebraic graphs and hypergraphs
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 24 October 2022, e95
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Percolation probability and critical exponents for site percolation on the UIPT
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 20 October 2022, pp. 1869-1903
- Print publication:
- December 2023
-
- Article
- Export citation
Graph distances in scale-free percolation: the logarithmic case
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 11 October 2022, pp. 295-313
- Print publication:
- March 2023
-
- Article
- Export citation
THE CHROMATIC NUMBER OF
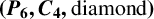 $\boldsymbol {(P_6,C_4,\mbox {diamond})}$-FREE GRAPHS
$\boldsymbol {(P_6,C_4,\mbox {diamond})}$-FREE GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 03 October 2022, pp. 1-10
- Print publication:
- August 2023
-
- Article
- Export citation
Spectra of infinite graphs via freeness with amalgamation
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 5 / October 2023
- Published online by Cambridge University Press:
- 03 October 2022, pp. 1633-1684
- Print publication:
- October 2023
-
- Article
- Export citation
Improved bound for improper colourings of graphs with no odd clique minor
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 30 September 2022, pp. 326-333
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Towards the 0-statement of the Kohayakawa-Kreuter conjecture
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 27 September 2022, pp. 225-268
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Irregular subgraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 23 September 2022, pp. 269-283
-
- Article
- Export citation
NOWHERE-ZERO
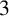 $3$-FLOWS IN TWO FAMILIES OF VERTEX-TRANSITIVE GRAPHS
$3$-FLOWS IN TWO FAMILIES OF VERTEX-TRANSITIVE GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 15 September 2022, pp. 353-360
- Print publication:
- June 2023
-
- Article
- Export citation
Uniqueness of the Gibbs measure for the 4-state anti-ferromagnetic Potts model on the regular tree
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 07 September 2022, pp. 158-182
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Small non-Leighton two-complexes
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 174 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 05 September 2022, pp. 385-391
- Print publication:
- March 2023
-
- Article
- Export citation
On connectivity and robustness of random graphs with inhomogeneity
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 60 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 05 September 2022, pp. 284-294
- Print publication:
- March 2023
-
- Article
- Export citation
Cycles of many lengths in Hamiltonian graphs
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 31 August 2022, e70
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Partial-dual polynomials and signed intersection graphs
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 25 August 2022, e69
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Surprising identities for the greedy independent set on Cayley trees
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 25 August 2022, pp. 1042-1058
- Print publication:
- December 2022
-
- Article
- Export citation
ON 2-TRANSITIVE SETS OF EQUIANGULAR LINES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 22 August 2022, pp. 134-145
- Print publication:
- February 2023
-
- Article
- Export citation
Degree sequences of sufficiently dense random uniform hypergraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 15 August 2022, pp. 183-224
-
- Article
- Export citation
ALMOST THEOREMS OF HYPERARITHMETIC ANALYSIS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 01 August 2022, pp. 664-696
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On local weak limit and subgraph counts for sparse random graphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 59 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 21 July 2022, pp. 755-776
- Print publication:
- September 2022
-
- Article
- Export citation