Refine listing
Actions for selected content:
1007 results in 05Cxx
The relationship between fixing subgraphs and smoothly embeddable subgraphs
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics / Volume 26 / Issue 3 / November 1978
- Published online by Cambridge University Press:
- 09 April 2009, pp. 353-367
- Print publication:
- November 1978
-
- Article
-
- You have access
- Export citation
Heawood's theorem and connectivity
- Part of
-
- Journal:
- Mathematika / Volume 20 / Issue 2 / December 1973
- Published online by Cambridge University Press:
- 26 February 2010, pp. 201-207
- Print publication:
- December 1973
-
- Article
- Export citation
The number of plane trees
- Part of
-
- Journal:
- Mathematika / Volume 19 / Issue 2 / December 1972
- Published online by Cambridge University Press:
- 26 February 2010, pp. 200-204
- Print publication:
- December 1972
-
- Article
- Export citation
Simple one-point extensions of tournaments
- Part of
-
- Journal:
- Mathematika / Volume 19 / Issue 1 / June 1972
- Published online by Cambridge University Press:
- 26 February 2010, pp. 57-62
- Print publication:
- June 1972
-
- Article
- Export citation
Properties and characterizations of k-trees
- Part of
-
- Journal:
- Mathematika / Volume 18 / Issue 1 / June 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 141-151
- Print publication:
- June 1971
-
- Article
- Export citation
Trees with Hamiltonian square
- Part of
-
- Journal:
- Mathematika / Volume 18 / Issue 1 / June 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 138-140
- Print publication:
- June 1971
-
- Article
- Export citation
The lengths of limbs of random trees
- Part of
-
- Journal:
- Mathematika / Volume 18 / Issue 1 / June 1971
- Published online by Cambridge University Press:
- 26 February 2010, pp. 78-81
- Print publication:
- June 1971
-
- Article
- Export citation

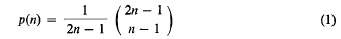
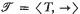 is a relational structure on the non-empty set
is a relational structure on the non-empty set 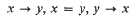
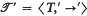 is a
is a 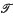 , and
, and 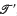 , if
, if 