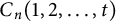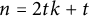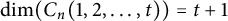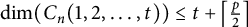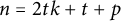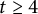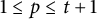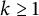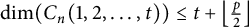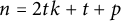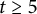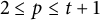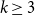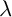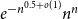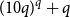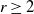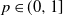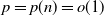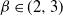Refine listing
Actions for selected content:
1007 results in 05Cxx
On the metric dimension of circulant graphs
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 28 September 2023, pp. 328-337
- Print publication:
- June 2024
-
- Article
- Export citation
Tower Gaps in Multicolour Ramsey Numbers
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 21 September 2023, e84
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the zeroes of hypergraph independence polynomials
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 21 September 2023, pp. 65-84
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CORRECTION TO ‘ON THE COMPLEMENT OF THE ZERO-DIVISOR GRAPH OF A PARTIALLY ORDERED SET’
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 18 September 2023, pp. 170-173
- Print publication:
- February 2024
-
- Article
- Export citation
CAYLEY GRAPHS AND GRAPHICAL REGULAR REPRESENTATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 15 September 2023, pp. 161-162
- Print publication:
- February 2024
-
- Article
-
- You have access
- HTML
- Export citation
COLORING ISOSCELES TRIANGLES IN CHOICELESS SET THEORY
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 11 September 2023, pp. 105-134
- Print publication:
- March 2025
-
- Article
- Export citation
ON THE DISTRIBUTION OF IWASAWA INVARIANTS ASSOCIATED TO MULTIGRAPHS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 253 / March 2024
- Published online by Cambridge University Press:
- 08 September 2023, pp. 48-90
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the size of maximal intersecting families
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 08 September 2023, pp. 32-49
-
- Article
- Export citation
Rotor-Routing Induces the Only Consistent Sandpile Torsor Structure on Plane Graphs
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 07 September 2023, e78
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Forcing generalised quasirandom graphs efficiently
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 33 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 05 September 2023, pp. 16-31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quantum symmetries of Cayley graphs of abelian groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 12 October 2023, pp. 655-686
- Print publication:
- September 2023
-
- Article
- Export citation
Subgraph distributions in dense random regular graphs
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 10 / October 2023
- Published online by Cambridge University Press:
- 25 August 2023, pp. 2125-2148
- Print publication:
- October 2023
-
- Article
- Export citation
Anticoncentration in Ramsey graphs and a proof of the Erdős–McKay conjecture
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 24 August 2023, e21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Normal and stable approximation to subgraph counts in superpositions of Bernoulli random graphs
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 61 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 18 August 2023, pp. 401-419
- Print publication:
- June 2024
-
- Article
- Export citation
Simple eigenvalues of cubic vertex-transitive graphs
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 10 August 2023, pp. 1496-1519
- Print publication:
- October 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The aromatic bicomplex for the description of divergence-free aromatic forms and volume-preserving integrators
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 08 August 2023, e69
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A modification of the random cutting model
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 07 August 2023, pp. 287-314
- Print publication:
- March 2024
-
- Article
- Export citation
Bootstrap percolation in inhomogeneous random graphs
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 56 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 07 August 2023, pp. 156-204
- Print publication:
- March 2024
-
- Article
- Export citation
Erdős–Ko–Rado theorem in Peisert-type graphs
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 04 August 2023, pp. 176-187
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Limiting empirical spectral distribution for the non-backtracking matrix of an Erdős-Rényi random graph
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 6 / November 2023
- Published online by Cambridge University Press:
- 31 July 2023, pp. 956-973
-
- Article
-
- You have access
- Open access
- HTML
- Export citation