Article contents
Local limits of spatial inhomogeneous random graphs
Published online by Cambridge University Press: 14 April 2023
Abstract
Consider a set of n vertices, where each vertex has a location in 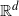 $\mathbb{R}^d$ that is sampled uniformly from the unit cube in
$\mathbb{R}^d$ that is sampled uniformly from the unit cube in 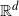 $\mathbb{R}^d$, and a weight associated to it. Construct a random graph by placing edges independently for each vertex pair with a probability that is a function of the distance between the locations and the vertex weights.
$\mathbb{R}^d$, and a weight associated to it. Construct a random graph by placing edges independently for each vertex pair with a probability that is a function of the distance between the locations and the vertex weights.
Under appropriate integrability assumptions on the edge probabilities that imply sparseness of the model, after appropriately blowing up the locations, we prove that the local limit of this random graph sequence is the (countably) infinite random graph on 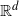 $\mathbb{R}^d$ with vertex locations given by a homogeneous Poisson point process, having weights which are independent and identically distributed copies of limiting vertex weights. Our set-up covers many sparse geometric random graph models from the literature, including geometric inhomogeneous random graphs (GIRGs), hyperbolic random graphs, continuum scale-free percolation, and weight-dependent random connection models.
$\mathbb{R}^d$ with vertex locations given by a homogeneous Poisson point process, having weights which are independent and identically distributed copies of limiting vertex weights. Our set-up covers many sparse geometric random graph models from the literature, including geometric inhomogeneous random graphs (GIRGs), hyperbolic random graphs, continuum scale-free percolation, and weight-dependent random connection models.
We prove that the limiting degree distribution is mixed Poisson and the typical degree sequence is uniformly integrable, and we obtain convergence results on various measures of clustering in our graphs as a consequence of local convergence. Finally, as a byproduct of our argument, we prove a doubly logarithmic lower bound on typical distances in this general setting.
MSC classification
Information
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Applied Probability Trust
References
- 5
- Cited by


