Hostname: page-component-745bb68f8f-cphqk Total loading time: 0 Render date: 2025-01-11T10:08:48.257Z Has data issue: false hasContentIssue false
  • English
  • Français

TRAVERSING A GRAPH IN GENERAL POSITION

Part of: Graph theory

Published online by Cambridge University Press:  13 February 2023

SANDI KLAVŽAR Open the ORCID record for SANDI KLAVŽAR [Opens in a new window] ,
ADITI KRISHNAKUMAR Open the ORCID record for ADITI KRISHNAKUMAR [Opens in a new window] ,
JAMES TUITE Open the ORCID record for JAMES TUITE [Opens in a new window]  and
ISMAEL G. YERO Open the ORCID record for ISMAEL G. YERO [Opens in a new window]
SANDI KLAVŽAR*
Affiliation:
Faculty of Mathematics and Physics, University of Ljubljana, Ljubljana, Slovenia; Institute of Mathematics, Physics and Mechanics, Ljubljana, Slovenia and Faculty of Natural Sciences and Mathematics, University of Maribor, Maribor, Slovenia
ADITI KRISHNAKUMAR
Affiliation:
Department of Mathematics and Statistics, Open University, Milton Keynes, UK e-mail: aditikrishnakumar@gmail.com
JAMES TUITE
Affiliation:
Department of Mathematics and Statistics, Open University, Milton Keynes, UK e-mail: james.t.tuite@open.ac.uk
ISMAEL G. YERO
Affiliation:
Departamento de Matemáticas, Universidad de Cádiz, Algeciras, Spain e-mail: ismael.gonzalez@uca.es
*
e-mail: sandi.klavzar@fmf.uni-lj.si
Get access Rights & Permissions [Opens in a new window]

Abstract

Let G be a graph. Assume that to each vertex of a set of vertices 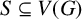$S\subseteq V(G)$ a robot is assigned. At each stage one robot can move to a neighbouring vertex. Then S is a mobile general position set of G if there exists a sequence of moves of the robots such that all the vertices of G are visited while maintaining the general position property at all times. The mobile general position number of G is the cardinality of a largest mobile general position set of G. We give bounds on the mobile general position number and determine exact values for certain common classes of graphs, including block graphs, rooted products, unicyclic graphs, Kneser graphs 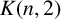$K(n,2)$ and line graphs of complete graphs.

Keywords

general position setmobile general position setmobile general position numberrobot navigationunicyclic graphKneser graph

MSC classification

Primary: 05C12: Distance in graphs
Secondary: 05C76: Graph operations (line graphs, products, etc.)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 108 , Issue 3 , December 2023 , pp. 353 - 365
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Sandi Klavžar was partially supported by the Slovenian Research Agency (ARRS) under grants P1-0297, J1-2452 and N1-0285. Ismael G. Yero has been partially supported by the Spanish Ministry of Science and Innovation through grant PID2019-105824GB-I00. James Tuite also gratefully acknowledges funding support from EPSRC grant EP/W522338/1.

References

Aljohani, A., Poudel, P. and Sharma, G., ‘Complete visitability for autonomous robots on graphs’, in: 2018 IEEE 32nd International Parallel and Distributed Processing Symposium, IPDPS 2018 (IEEE Computer Society, Piscataway, NJ, 2018), 733–742.Google Scholar
Aljohani, A. and Sharma, G., ‘Complete visibility for mobile robots with lights tolerating faults’, Int. J. Netw. Comput. 8 (2018), 32–52.Google Scholar
Anand, B. S., Chandran, S. V. U., Changat, M., Klavžar, S. and Thomas, E. J., ‘Characterization of general position sets and its applications to cographs and bipartite graphs’, Appl. Math. Comput. 359 (2019), 84–89.10.1016/j.amc.2019.04.064CrossRefGoogle Scholar
Di Luna, G. A., Flocchini, P., Chaudhuri, S. G., Poloni, F., Santoro, N. and Viglietta, G., ‘Mutual visibility by luminous robots without collisions’, Inf. Comput. 254 (2017), 392–418.10.1016/j.ic.2016.09.005CrossRefGoogle Scholar
Ghorbani, M., Klavžar, S., Maimani, H. R., Momeni, M., Rahimi-Mahid, F. and Rus, G., ‘The general position problem on Kneser graphs and on some graph operations’, Discuss. Math. Graph Theory 41 (2021), 1199–1213.10.7151/dmgt.2269CrossRefGoogle Scholar
Klavžar, S., Patkós, B., Rus, G. and Yero, I. G., ‘On general position sets in Cartesian products’, Results Math. 76 (2021), Article no. 123.10.1007/s00025-021-01438-xCrossRefGoogle Scholar
Körner, J., ‘On the extremal combinatorics of the Hamming space’, J. Combin. Theory Ser. A 71 (1995), 112–126.10.1016/0097-3165(95)90019-5CrossRefGoogle Scholar
Manuel, P. and Klavžar, S.. ‘A general position problem in graph theory’, Bull. Aust. Math. Soc. 98 (2018), 177–187.10.1017/S0004972718000473CrossRefGoogle Scholar
Pálvölgyi, D. and Gyárfás, A., ‘Domination in transitive colorings of tournaments’, J. Combin. Theory Ser. B 107 (2014), 1–11.10.1016/j.jctb.2014.02.001CrossRefGoogle Scholar
Patkós, B., ‘On the general position problem on Kneser graphs’, Ars Math. Contemp. 18 (2020), 273–280.10.26493/1855-3974.1957.a0fCrossRefGoogle Scholar
Tian, J. and Xu, K., ‘The general position number of Cartesian products involving a factor with small diameter’, Appl. Math. Comput. 403 (2021), Article no. 126206.10.1016/j.amc.2021.126206CrossRefGoogle Scholar
Tian, J., Xu, K. and Klavžar, S., ‘The general position number of Cartesian product of two trees’, Bull. Aust. Math. Soc. 104 (2021), 1–10.10.1017/S0004972720001276CrossRefGoogle Scholar
Ullas Chandran, S. V. and Parthasarathy, G. J., ‘The geodesic irredundant sets in graphs’, Int. J. Math. Combin. 4 (2016), 135–143.Google Scholar
Website Starship, https://www.starship.xyz/ (accessed on 22 September 2022).Google Scholar
Yao, Y., He, M. and Ji, S., ‘On the general position number of two classes of graphs’, Open Math. 20 (2022), 1021–1029.10.1515/math-2022-0444CrossRefGoogle Scholar