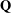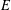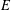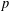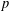Refine listing
Actions for selected content:
531 results in 11Gxx
COUNTING POINTS ON DWORK HYPERSURFACES AND
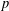 $p$ -ADIC HYPERGEOMETRIC FUNCTIONS
$p$ -ADIC HYPERGEOMETRIC FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 94 / Issue 2 / October 2016
- Published online by Cambridge University Press:
- 17 February 2016, pp. 208-216
- Print publication:
- October 2016
-
- Article
-
- You have access
- Export citation
ON THE EXCEPTIONAL SPECIALIZATIONS OF BIG HEEGNER POINTS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 17 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 04 February 2016, pp. 207-240
- Print publication:
- February 2018
-
- Article
- Export citation
COMPUTING IMAGES OF GALOIS REPRESENTATIONS ATTACHED TO ELLIPTIC CURVES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 02 February 2016, e4
-
- Article
-
- You have access
- Open access
- Export citation
On the Oort conjecture for Shimura varieties of unitary and orthogonal types
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 5 / May 2016
- Published online by Cambridge University Press:
- 02 February 2016, pp. 889-917
- Print publication:
- May 2016
-
- Article
- Export citation
COMPACTIFICATIONS OF PEL-TYPE SHIMURA VARIETIES IN RAMIFIED CHARACTERISTICS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 05 January 2016, e1
-
- Article
-
- You have access
- Open access
- Export citation
THE PROPORTION OF FAILURES OF THE HASSE NORM PRINCIPLE
- Part of
-
- Journal:
- Mathematika / Volume 62 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 22 January 2016, pp. 337-347
- Print publication:
- 2016
-
- Article
- Export citation
Strict supports of canonical measures and applications to the geometric Bogomolov conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 5 / May 2016
- Published online by Cambridge University Press:
- 22 December 2015, pp. 997-1040
- Print publication:
- May 2016
-
- Article
- Export citation
Integral canonical models for Spin Shimura varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 4 / April 2016
- Published online by Cambridge University Press:
- 07 December 2015, pp. 769-824
- Print publication:
- April 2016
-
- Article
- Export citation
Good families of Drinfeld modular curves
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 December 2015, pp. 699-712
-
- Article
-
- You have access
- Export citation
Integral points of bounded degree on affine curves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 4 / April 2016
- Published online by Cambridge University Press:
- 26 November 2015, pp. 754-768
- Print publication:
- April 2016
-
- Article
- Export citation
CERTAIN GENERALIZED MORDELL CURVES OVER THE RATIONAL NUMBERS ARE POINTLESS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 28 October 2015, pp. 42-64
- Print publication:
- February 2016
-
- Article
-
- You have access
- Export citation
STARK POINTS AND
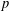 $p$-ADIC ITERATED INTEGRALS ATTACHED TO MODULAR FORMS OF WEIGHT ONE
$p$-ADIC ITERATED INTEGRALS ATTACHED TO MODULAR FORMS OF WEIGHT ONE
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 3 / 2015
- Published online by Cambridge University Press:
- 13 October 2015, e8
-
- Article
-
- You have access
- Open access
- Export citation
Simply connected varieties in characteristic
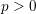 $p>0$
$p>0$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 2 / February 2016
- Published online by Cambridge University Press:
- 09 October 2015, pp. 255-287
- Print publication:
- February 2016
-
- Article
- Export citation
CATEGORICITY OF MODULAR AND SHIMURA CURVES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 16 / Issue 5 / November 2017
- Published online by Cambridge University Press:
- 30 September 2015, pp. 1075-1101
- Print publication:
- November 2017
-
- Article
- Export citation
The Chowla–Selberg formula for abelian CM fields and Faltings heights
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 3 / March 2016
- Published online by Cambridge University Press:
- 24 September 2015, pp. 445-476
- Print publication:
- March 2016
-
- Article
- Export citation
Mordell’s equation: a classical approach
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 September 2015, pp. 633-646
-
- Article
-
- You have access
- Export citation
p-adic Eisenstein-Kronecker series for CM elliptic curves and the Kronecker limit formulas
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 219 / September 2015
- Published online by Cambridge University Press:
- 11 January 2016, pp. 269-302
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
PARAMETRIZING ELLIPTIC CURVES BY MODULAR UNITS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 100 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 19 August 2015, pp. 33-41
- Print publication:
- February 2016
-
- Article
-
- You have access
- Export citation
NON-ARCHIMEDEAN YOMDIN–GROMOV PARAMETRIZATIONS AND POINTS OF BOUNDED HEIGHT
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 3 / 2015
- Published online by Cambridge University Press:
- 14 August 2015, e5
-
- Article
-
- You have access
- Open access
- Export citation
Formal Fourier Jacobi expansions and special cycles of codimension two
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 12 / December 2015
- Published online by Cambridge University Press:
- 06 August 2015, pp. 2187-2211
- Print publication:
- December 2015
-
- Article
- Export citation
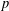
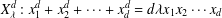
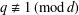
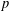
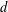
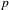
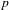

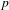
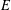
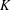
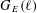
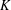
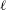
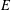
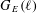
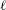
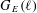
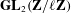
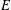

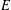

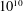
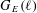
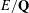
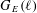
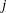
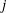
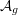
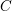
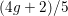
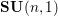
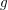
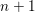
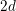
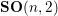
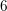
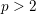
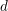
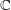
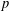
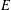
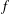
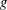
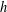
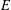
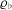
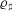
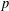
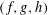
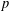
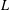
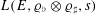
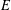
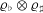
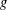
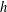
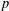
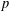
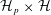
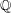
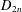
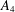
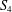
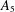
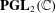
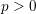
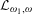
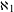
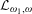
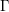
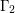
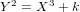

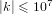
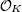 of K. In this paper, we construct
of K. In this paper, we construct