Refine listing
Actions for selected content:
530 results in 11Gxx
The arithmetic of Prym varieties in genus 3
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 2 / March 2008
- Published online by Cambridge University Press:
- 01 March 2008, pp. 317-338
- Print publication:
- March 2008
-
- Article
-
- You have access
- Export citation
Counting Rational Points on Cubic Hypersurfaces
- Part of
-
- Journal:
- Mathematika / Volume 54 / Issue 1-2 / December 2007
- Published online by Cambridge University Press:
- 21 December 2009, pp. 93-112
- Print publication:
- December 2007
-
- Article
- Export citation
On Rubin’s variant of the p-adic Birch and Swinnerton-Dyer conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 143 / Issue 6 / November 2007
- Published online by Cambridge University Press:
- 01 November 2007, pp. 1374-1398
- Print publication:
- November 2007
-
- Article
-
- You have access
- Export citation
A Dirichlet series expansion for the p-adic zeta-function
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 81 / Issue 2 / October 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 215-224
- Print publication:
- October 2006
-
- Article
-
- You have access
- Export citation
Zeta functions of twisted modular curves
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 80 / Issue 1 / February 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 89-103
- Print publication:
- February 2006
-
- Article
-
- You have access
- Export citation
On the Quadratic Twists of a Family of Elliptic Curves
- Part of
-
- Journal:
- Mathematika / Volume 52 / Issue 1-2 / December 2005
- Published online by Cambridge University Press:
- 21 December 2009, pp. 139-154
- Print publication:
- December 2005
-
- Article
- Export citation
Integral points on elliptic curves over function fields
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 77 / Issue 2 / October 2004
- Published online by Cambridge University Press:
- 09 April 2009, pp. 197-208
- Print publication:
- October 2004
-
- Article
-
- You have access
- Export citation
Independance algebrique des derivees d'une periode du module de Carlitz
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 69 / Issue 1 / August 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 8-18
- Print publication:
- August 2000
-
- Article
-
- You have access
- Export citation
Multiplicative isogeny estimates
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 64 / Issue 2 / April 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 178-194
- Print publication:
- April 1998
-
- Article
-
- You have access
- Export citation
Integer points on algebraic curves with exceptional units
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 63 / Issue 2 / October 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 145-164
- Print publication:
- October 1997
-
- Article
-
- You have access
- Export citation
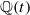 . By specialization, this also gives examples over
. By specialization, this also gives examples over 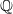 .
.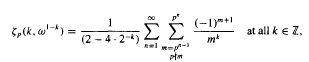 Where the convergence of the first summation is for the
Where the convergence of the first summation is for the