Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Shapiro, I.
2009.
Frobenius Map for Quintic Threefolds.
International Mathematics Research Notices,
Delbourgo, Daniel
and
Chao, Qin
2015.
On -invariants attached to cyclic cubic number fields.
LMS Journal of Computation and Mathematics,
Vol. 18,
Issue. 1,
p.
684.
Yavuz, Enes
2019.
On the resummation of series of fuzzy numbers via generalized Dirichlet and generalized factorial series.
Journal of Intelligent & Fuzzy Systems,
Vol. 37,
Issue. 6,
p.
8199.
Alharbi, Nof
Kammoun, Rania
and
Ozel, Cenap
2019.
p-Adic Zeroes of the Kubota-Leopoldt Zeta-Function.
p-Adic Numbers, Ultrametric Analysis and Applications,
Vol. 11,
Issue. 4,
p.
255.
Knospe, Heiko
and
Washington, Lawrence C.
2021.
Dirichlet series expansions of p-adic L-functions.
Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg,
Vol. 91,
Issue. 2,
p.
325.
Zhao, Luochen
2022.
Sum expressions for Kubota–Leopoldt -adic -functions.
Proceedings of the Edinburgh Mathematical Society,
Vol. 65,
Issue. 2,
p.
460.
Zhao, Luochen
2022.
Note on $$p$$-Adic Local Functional Equation.
p-Adic Numbers, Ultrametric Analysis and Applications,
Vol. 14,
Issue. 3,
p.
238.
Delbourgo, Daniel
and
Knospe, Heiko
2023.
On Iwasawa 𝜆-invariants for abelian number fields and random matrix heuristics.
Mathematics of Computation,
Vol. 92,
Issue. 342,
p.
1817.

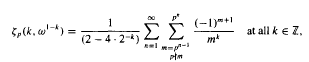 Where the convergence of the first summation is for the
Where the convergence of the first summation is for the