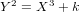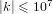Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bennett, Michael A.
and
Scheerer, Adrian-Maria
2017.
Number Theory – Diophantine Problems, Uniform Distribution and Applications.
p.
83.
Bennett, Michael A.
and
Rechnitzer, Andrew
2017.
Recent Progress and Modern Challenges in Applied Mathematics, Modeling and Computational Science.
Vol. 79,
Issue. ,
p.
387.
Bennett, Michael
Bruni, Carmen
and
Freitas, Nuno
2018.
Sums of two cubes as twisted perfect powers, revisited.
Algebra & Number Theory,
Vol. 12,
Issue. 4,
p.
959.
Gaál, István
Pohst, Maximilian C.
and
Pohst, Michael E.
2021.
On computing integral points of a Mordell curve – the method of Wildanger revisited.
Experimental Mathematics,
Vol. 30,
Issue. 1,
p.
127.
Klaška, Jiří
2022.
Quartic Polynomials with a Given Discriminant.
Mathematica Slovaca,
Vol. 72,
Issue. 1,
p.
35.
Baanen, Anne
Best, Alex J.
Coppola, Nirvana
and
Dahmen, Sander R.
2023.
Formalized Class Group Computations and Integral Points on Mordell Elliptic Curves.
p.
47.
von Känel, Rafael
and
Matschke, Benjamin
2023.
Solving 𝑆-unit, Mordell, Thue, Thue–Mahler and Generalized Ramanujan–Nagell Equations via the Shimura–Taniyama Conjecture.
Memoirs of the American Mathematical Society,
Vol. 286,
Issue. 1419,
Cazorla García, Pedro-José
2024.
Perfect Codes over Non-Prime Power Alphabets: An Approach Based on Diophantine Equations.
Mathematics,
Vol. 12,
Issue. 11,
p.
1642.
Chan, Stephanie
2024.
Integral points on cubic twists of Mordell curves.
Mathematische Annalen,
Vol. 388,
Issue. 3,
p.
2275.
Grechuk, Bogdan
2024.
Polynomial Diophantine Equations.
p.
107.
Reynya, Mikhail A.
2024.
A two-parametric family of high rank Mordell curves.
International Journal of Number Theory,
Vol. 20,
Issue. 03,
p.
821.
von Känel, Rafael
2025.
Integral points on moduli schemes.
Journal of Number Theory,
Vol. 270,
Issue. ,
p.
167.