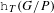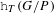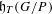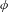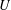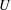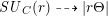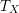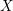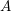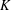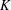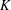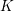Refine listing
Actions for selected content:
181 results in 14Mxx
The Cohomology Groups of Real Toric Varieties Associated with Weyl Chambers of Types C and D
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 3 / August 2019
- Published online by Cambridge University Press:
- 14 February 2019, pp. 861-874
-
- Article
- Export citation
PARABOLIC KAZHDAN–LUSZTIG BASIS, SCHUBERT CLASSES, AND EQUIVARIANT ORIENTED COHOMOLOGY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 6 / November 2020
- Published online by Cambridge University Press:
- 11 February 2019, pp. 1889-1929
- Print publication:
- November 2020
-
- Article
- Export citation
Examples of Non-finitely Generated Cox Rings
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 267-285
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
Dynamical degrees of Hurwitz correspondences
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 7 / July 2020
- Published online by Cambridge University Press:
- 04 December 2018, pp. 1968-1990
- Print publication:
- July 2020
-
- Article
- Export citation
NOTES ON TORIC VARIETIES FROM MORI THEORETIC VIEWPOINT, II
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 239 / September 2020
- Published online by Cambridge University Press:
- 29 August 2018, pp. 42-75
- Print publication:
- September 2020
-
- Article
-
- You have access
- HTML
- Export citation
The vanishing cycles of curves in toric surfaces I
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 8 / August 2018
- Published online by Cambridge University Press:
- 18 July 2018, pp. 1659-1697
- Print publication:
- August 2018
-
- Article
- Export citation
Chern class formulas for classical-type degeneracy loci
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 8 / August 2018
- Published online by Cambridge University Press:
- 18 July 2018, pp. 1746-1774
- Print publication:
- August 2018
-
- Article
- Export citation
LOCAL SYSTEMS ON COMPLEMENTS OF ARRANGEMENTS OF SMOOTH, COMPLEX ALGEBRAIC HYPERSURFACES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 6 / 2018
- Published online by Cambridge University Press:
- 23 May 2018, e6
-
- Article
-
- You have access
- Open access
- Export citation
Sums of three squares and Noether–Lefschetz loci
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 5 / May 2018
- Published online by Cambridge University Press:
- 03 April 2018, pp. 1048-1065
- Print publication:
- May 2018
-
- Article
- Export citation
GRASSMANNIAN SEMIGROUPS AND THEIR REPRESENTATIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 104 / Issue 3 / June 2018
- Published online by Cambridge University Press:
- 27 March 2018, pp. 308-337
- Print publication:
- June 2018
-
- Article
-
- You have access
- Export citation
Strong cohomological rigidity of toric varieties
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 5 / October 2017
- Published online by Cambridge University Press:
- 25 September 2017, pp. 971-992
- Print publication:
- October 2017
-
- Article
- Export citation
Tangent cones to generalised theta divisors and generic injectivity of the theta map
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 12 / December 2017
- Published online by Cambridge University Press:
- 13 September 2017, pp. 2643-2657
- Print publication:
- December 2017
-
- Article
- Export citation
CHARACTERIZATION OF PROJECTIVE SPACES AND
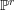 $\mathbb{P}^{r}$-BUNDLES AS AMPLE DIVISORS
$\mathbb{P}^{r}$-BUNDLES AS AMPLE DIVISORS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 233 / March 2019
- Published online by Cambridge University Press:
- 08 September 2017, pp. 155-169
- Print publication:
- March 2019
-
- Article
-
- You have access
- HTML
- Export citation
THE SHORT RESOLUTION OF A SEMIGROUP ALGEBRA
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 3 / December 2017
- Published online by Cambridge University Press:
- 29 August 2017, pp. 400-411
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation
Équivalence motivique des groupes algébriques semisimples
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 10 / October 2017
- Published online by Cambridge University Press:
- 27 July 2017, pp. 2195-2213
- Print publication:
- October 2017
-
- Article
- Export citation
ON VANISHING THEOREMS FOR LOCAL SYSTEMS ASSOCIATED TO LAURENT POLYNOMIALS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 231 / September 2018
- Published online by Cambridge University Press:
- 18 July 2017, pp. 1-22
- Print publication:
- September 2018
-
- Article
-
- You have access
- HTML
- Export citation
EQUIVARIANT
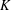 $K$ -THEORY OF GRASSMANNIANS
$K$ -THEORY OF GRASSMANNIANS
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 5 / 2017
- Published online by Cambridge University Press:
- 27 June 2017, e3
-
- Article
-
- You have access
- Open access
- Export citation
FROM COMPLETE TO PARTIAL FLAGS IN GEOMETRIC EXTENSION ALGEBRAS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 60 / Issue 1 / January 2018
- Published online by Cambridge University Press:
- 13 March 2017, pp. 111-121
- Print publication:
- January 2018
-
- Article
-
- You have access
- Export citation
Equivariant
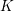 $K$ -theory of Grassmannians II: the Knutson–Vakil conjecture
$K$ -theory of Grassmannians II: the Knutson–Vakil conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 4 / April 2017
- Published online by Cambridge University Press:
- 09 March 2017, pp. 667-677
- Print publication:
- April 2017
-
- Article
- Export citation
Differential Graded Quivers of Smooth Rational Surfaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 15 December 2016, pp. 859-876
-
- Article
- Export citation