No CrossRef data available.
Article contents
GRASSMANNIAN SEMIGROUPS AND THEIR REPRESENTATIONS
Published online by Cambridge University Press: 27 March 2018
Abstract
The set of row reduced matrices (and of echelon form matrices) is closed under multiplication. We show that any system of representatives for the 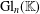 $\text{Gl}_{n}(\mathbb{K})$ action on the
$\text{Gl}_{n}(\mathbb{K})$ action on the 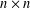 $n\times n$ matrices, which is closed under multiplication, is necessarily conjugate to one that is in simultaneous echelon form. We call such closed representative systems Grassmannian semigroups. We study internal properties of such Grassmannian semigroups and show that they are algebraic semigroups and admit gradings by the finite semigroup of partial order preserving permutations, with components that are naturally in one–one correspondence with the Schubert cells of the total Grassmannian. We show that there are infinitely many isomorphism types of such semigroups in general, and two such semigroups are isomorphic exactly when they are semiconjugate in
$n\times n$ matrices, which is closed under multiplication, is necessarily conjugate to one that is in simultaneous echelon form. We call such closed representative systems Grassmannian semigroups. We study internal properties of such Grassmannian semigroups and show that they are algebraic semigroups and admit gradings by the finite semigroup of partial order preserving permutations, with components that are naturally in one–one correspondence with the Schubert cells of the total Grassmannian. We show that there are infinitely many isomorphism types of such semigroups in general, and two such semigroups are isomorphic exactly when they are semiconjugate in 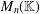 $M_{n}(\mathbb{K})$ . We also investigate their representation theory over an arbitrary field, and other connections with multiplicative structures on Grassmannians and Young diagrams.
$M_{n}(\mathbb{K})$ . We also investigate their representation theory over an arbitrary field, and other connections with multiplicative structures on Grassmannians and Young diagrams.
Information
- Type
- Research Article
- Information
- Copyright
- © 2018 Australian Mathematical Publishing Association Inc.

