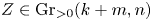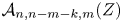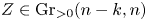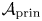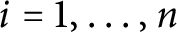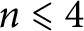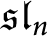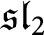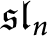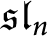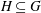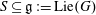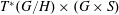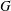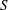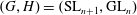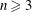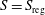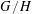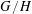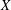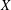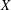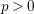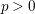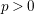Refine listing
Actions for selected content:
181 results in 14Mxx
Minimal rational curves on generalized Bott–Samelson varieties
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 15 February 2021, pp. 122-153
- Print publication:
- January 2021
-
- Article
- Export citation
Equivariant cohomology of torus orbifolds
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 20 November 2020, pp. 299-328
- Print publication:
- April 2022
-
- Article
- Export citation
Parity duality for the amplituhedron
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 11 / November 2020
- Published online by Cambridge University Press:
- 09 December 2020, pp. 2207-2262
- Print publication:
- November 2020
-
- Article
- Export citation
Tropical geometry and Newton–Okounkov cones for Grassmannian of planes from compactifications
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 12 October 2020, pp. 199-231
- Print publication:
- February 2022
-
- Article
- Export citation
Toric degenerations of cluster varieties and cluster duality
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 10 / October 2020
- Published online by Cambridge University Press:
- 07 December 2020, pp. 2149-2206
- Print publication:
- October 2020
-
- Article
- Export citation
On a rationality problem for fields of cross-ratios II
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 04 September 2020, pp. 667-677
- Print publication:
- September 2021
-
- Article
- Export citation
THE COMBINATORICS OF TENSOR PRODUCTS OF HIGHER AUSLANDER ALGEBRAS OF TYPE A
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 29 July 2020, pp. 526-546
- Print publication:
- September 2021
-
- Article
- Export citation
Dynamical invariants of monomial correspondences
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 7 / July 2021
- Published online by Cambridge University Press:
- 02 June 2020, pp. 2000-2015
- Print publication:
- July 2021
-
- Article
- Export citation
Categorification via blocks of modular representations for
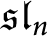 $\mathfrak {sl}_n$
$\mathfrak {sl}_n$
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 19 May 2020, pp. 1095-1123
- Print publication:
- August 2021
-
- Article
-
- You have access
- Open access
- Export citation
SYMBOLIC ANALYTIC SPREAD: UPPER BOUNDS AND APPLICATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 6 / November 2021
- Published online by Cambridge University Press:
- 07 May 2020, pp. 1969-1981
- Print publication:
- November 2021
-
- Article
- Export citation
An Application of Spherical Geometry to Hyperkähler Slices
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 24 February 2020, pp. 687-716
- Print publication:
- June 2021
-
- Article
- Export citation
On the non-divisorial base locus of big and nef line bundles on K3[2]-type varieties
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 20 February 2020, pp. 52-78
- Print publication:
- February 2021
-
- Article
- Export citation
THE INTERSECTION MOTIVE OF THE MODULI STACK OF SHTUKAS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 03 February 2020, e8
-
- Article
-
- You have access
- Open access
- Export citation
Relative Equivariant Motives and Modules
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 08 November 2019, pp. 131-159
- Print publication:
- February 2021
-
- Article
- Export citation
ON TORUS ACTIONS OF HIGHER COMPLEXITY
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 31 October 2019, e38
-
- Article
-
- You have access
- Open access
- Export citation
Residual intersections are Koszul–Fitting ideals
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 11 / November 2019
- Published online by Cambridge University Press:
- 23 September 2019, pp. 2150-2179
- Print publication:
- November 2019
-
- Article
- Export citation
Poincaré duality and resonance varieties
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 13 September 2019, pp. 3001-3027
- Print publication:
- December 2020
-
- Article
- Export citation
A FILTRATION ON EQUIVARIANT BOREL–MOORE HOMOLOGY
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 04 July 2019, e18
-
- Article
-
- You have access
- Open access
- Export citation
Nef anti-canonical divisors and rationally connected fibrations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 7 / July 2019
- Published online by Cambridge University Press:
- 28 June 2019, pp. 1444-1456
- Print publication:
- July 2019
-
- Article
- Export citation
ON VARIETIES WITH TRIVIAL TANGENT BUNDLE IN CHARACTERISTIC
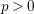 $p>0$
$p>0$
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 242 / June 2021
- Published online by Cambridge University Press:
- 26 June 2019, pp. 35-51
- Print publication:
- June 2021
-
- Article
- Export citation