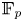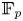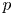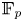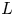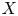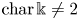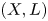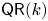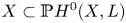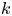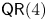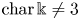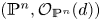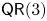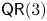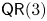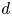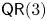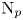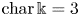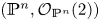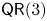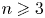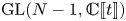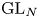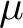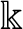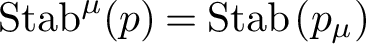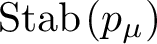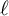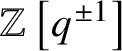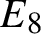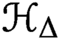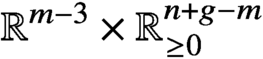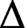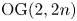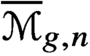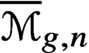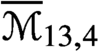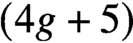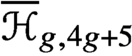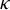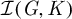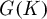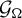Refine listing
Actions for selected content:
181 results in 14Mxx
Central elements in affine mod p Hecke algebras via perverse
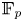 $\mathbb {F}_p$-sheaves
$\mathbb {F}_p$-sheaves
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 10 / October 2021
- Published online by Cambridge University Press:
- 14 September 2021, pp. 2215-2241
- Print publication:
- October 2021
-
- Article
- Export citation
Fano-type surfaces with large cyclic automorphisms
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 05 August 2021, e54
-
- Article
-
- You have access
- Open access
- Export citation
Rank 3 quadratic generators of Veronese embeddings
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 9 / September 2021
- Published online by Cambridge University Press:
- 02 August 2021, pp. 2001-2025
- Print publication:
- September 2021
-
- Article
- Export citation
Mirabolic Satake equivalence and supergroups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 8 / August 2021
- Published online by Cambridge University Press:
- 22 July 2021, pp. 1724-1765
- Print publication:
- August 2021
-
- Article
- Export citation
PETERZIL–STEINHORN SUBGROUPS AND
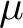 $\mu $-STABILIZERS IN ACF
$\mu $-STABILIZERS IN ACF
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 21 July 2021, pp. 1003-1022
- Print publication:
- May 2023
-
- Article
- Export citation
THE GENERIC FIBRE OF MODULI SPACES OF BOUNDED LOCAL G-SHTUKAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 2 / March 2023
- Published online by Cambridge University Press:
- 12 July 2021, pp. 799-878
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Inverse K-Chevalley formulas for semi-infinite flag manifolds, I: minuscule weights in ADE type
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 07 July 2021, e51
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The cohomology rings of real toric spaces and smooth real toric varieties
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 29 June 2021, pp. 720-737
- Print publication:
- June 2022
-
- Article
- Export citation
Smoothing Calabi–Yau toric hypersurfaces using the Gross–Siebert algorithm
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 7 / July 2021
- Published online by Cambridge University Press:
- 17 June 2021, pp. 1441-1491
- Print publication:
- July 2021
-
- Article
- Export citation
REPRESENTATION VARIETIES OF ALGEBRAS WITH NODES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 15 June 2021, pp. 2215-2245
- Print publication:
- November 2022
-
- Article
- Export citation
SMOOTH FANO 4-FOLDS IN GORENSTEIN FORMATS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 31 May 2021, pp. 424-433
- Print publication:
- December 2021
-
- Article
- Export citation
The moduli space of Harnack curves in toric surfaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 27 May 2021, e43
-
- Article
-
- You have access
- Open access
- Export citation
Beilinson–Drinfeld Schubert varieties and global Demazure modules
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 25 May 2021, e42
-
- Article
-
- You have access
- Open access
- Export citation
Residual categories for (co)adjoint Grassmannians in classical types
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 6 / June 2021
- Published online by Cambridge University Press:
- 20 May 2021, pp. 1172-1206
- Print publication:
- June 2021
-
- Article
- Export citation
Involution pipe dreams
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 5 / October 2022
- Published online by Cambridge University Press:
- 14 May 2021, pp. 1310-1346
- Print publication:
- October 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Back stable Schubert calculus
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 5 / May 2021
- Published online by Cambridge University Press:
- 30 April 2021, pp. 883-962
- Print publication:
- May 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Pencils on Surfaces with Normal Crossings and the Kodaira Dimension of
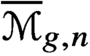 $\overline {\mathcal {M}}_{g,n}$
$\overline {\mathcal {M}}_{g,n}$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 12 April 2021, e31
-
- Article
-
- You have access
- Open access
- Export citation
POWERS OF BINOMIAL EDGE IDEALS WITH QUADRATIC GRÖBNER BASES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 246 / June 2022
- Published online by Cambridge University Press:
- 31 March 2021, pp. 233-255
- Print publication:
- June 2022
-
- Article
- Export citation
UNIRATIONALITY AND GEOMETRIC UNIRATIONALITY FOR HYPERSURFACES IN POSITIVE CHARACTERISTICS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 08 March 2021, pp. 1831-1847
- Print publication:
- September 2022
-
- Article
- Export citation
THÉORIE DE BRUHAT-TITS POUR LES GROUPES QUASI-RÉDUCTIFS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 4 / July 2022
- Published online by Cambridge University Press:
- 25 January 2021, pp. 1331-1362
- Print publication:
- July 2022
-
- Article
- Export citation