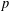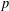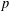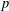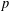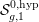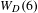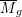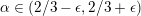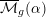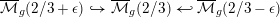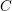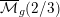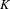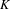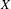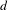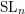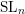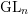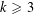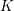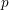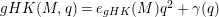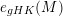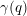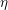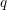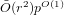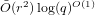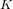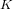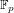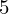Refine listing
Actions for selected content:
294 results in 14Hxx
TRANSPORT PARALLÈLE ET CORRESPONDANCE DE SIMPSON
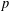 $p$ -ADIQUE
$p$ -ADIQUE
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 5 / 2017
- Published online by Cambridge University Press:
- 19 June 2017, e13
-
- Article
-
- You have access
- Open access
- Export citation
THE RATIONALITY OF THE MODULI SPACE OF ONE-POINTED INEFFECTIVE SPIN HYPERELLIPTIC CURVES VIA AN ALMOST DEL PEZZO THREEFOLD
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 232 / December 2018
- Published online by Cambridge University Press:
- 06 June 2017, pp. 121-150
- Print publication:
- December 2018
-
- Article
-
- You have access
- HTML
- Export citation
ORBIFOLD POINTS ON PRYM–TEICHMÜLLER CURVES IN GENUS
 $4$
$4$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 4 / July 2019
- Published online by Cambridge University Press:
- 22 May 2017, pp. 673-706
- Print publication:
- July 2019
-
- Article
- Export citation
Second flip in the Hassett–Keel program: a local description
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 8 / August 2017
- Published online by Cambridge University Press:
- 18 May 2017, pp. 1547-1583
- Print publication:
- August 2017
-
- Article
- Export citation
Second flip in the Hassett–Keel program: existence of good moduli spaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 8 / August 2017
- Published online by Cambridge University Press:
- 15 May 2017, pp. 1584-1609
- Print publication:
- August 2017
-
- Article
- Export citation
VANISHING OF THE NEGATIVE HOMOTOPY
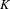 $K$-THEORY OF QUOTIENT SINGULARITIES
$K$-THEORY OF QUOTIENT SINGULARITIES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 3 / May 2019
- Published online by Cambridge University Press:
- 08 May 2017, pp. 619-627
- Print publication:
- May 2019
-
- Article
- Export citation
A support theorem for the Hitchin fibration: the case of
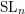 $\text{SL}_{n}$
$\text{SL}_{n}$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 6 / June 2017
- Published online by Cambridge University Press:
- 26 April 2017, pp. 1316-1347
- Print publication:
- June 2017
-
- Article
- Export citation
OBSTRUCTION THEORY FOR SUPERMANIFOLDS AND DEFORMATIONS OF SUPERCONFORMAL STRUCTURES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 15 March 2017, pp. 512-514
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
Picard curves over
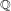 $\mathbb{Q}$ with good reduction away from 3
$\mathbb{Q}$ with good reduction away from 3
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue 2 / 2016
- Published online by Cambridge University Press:
- 01 March 2017, pp. 382-408
-
- Article
-
- You have access
- Export citation
The extremal secant conjecture for curves of arbitrary gonality
- Part of
-
- Journal:
- Compositio Mathematica / Volume 153 / Issue 2 / February 2017
- Published online by Cambridge University Press:
- 06 February 2017, pp. 347-357
- Print publication:
- February 2017
-
- Article
- Export citation
A LOWER BOUND FOR THE GONALITY CONJECTURE
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 2 / 2017
- Published online by Cambridge University Press:
- 03 April 2017, pp. 561-563
- Print publication:
- 2017
-
- Article
- Export citation
GENERALIZED HILBERT–KUNZ FUNCTION IN GRADED DIMENSION 2
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 230 / June 2018
- Published online by Cambridge University Press:
- 05 December 2016, pp. 1-17
- Print publication:
- June 2018
-
- Article
-
- You have access
- HTML
- Export citation
A VANISHING THEOREM FOR THE
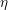 $\unicode[STIX]{x1D702}$ -INVARIANT AND HURWITZ GROUPS
$\unicode[STIX]{x1D702}$ -INVARIANT AND HURWITZ GROUPS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 228 / December 2017
- Published online by Cambridge University Press:
- 20 October 2016, pp. 114-123
- Print publication:
- December 2017
-
- Article
-
- You have access
- HTML
- Export citation
ALBANESE VARIETIES OF CYCLIC COVERS OF THE PROJECTIVE PLANE AND ORBIFOLD PENCILS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 227 / September 2017
- Published online by Cambridge University Press:
- 05 October 2016, pp. 189-213
- Print publication:
- September 2017
-
- Article
-
- You have access
- HTML
- Export citation
Explicit isogenies in quadratic time in any characteristic
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 267-282
-
- Article
-
- You have access
- Export citation
A database of genus-2 curves over the rational numbers
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 235-254
-
- Article
-
- You have access
- Export citation
JKL-ECM: an implementation of ECM using Hessian curves
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 83-99
-
- Article
-
- You have access
- Export citation
Computing theta functions in quasi-linear time in genus two and above
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 163-177
-
- Article
-
- You have access
- Export citation
Constructing genus-3 hyperelliptic Jacobians with CM
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 283-300
-
- Article
-
- You have access
- Export citation
Real multiplication through explicit correspondences
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 19 / Issue A / 2016
- Published online by Cambridge University Press:
- 26 August 2016, pp. 29-42
-
- Article
-
- You have access
- Export citation