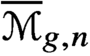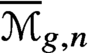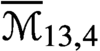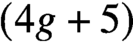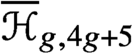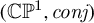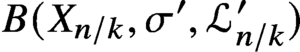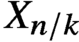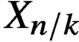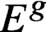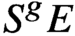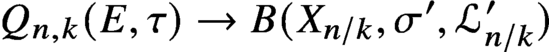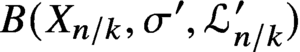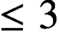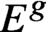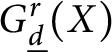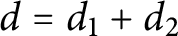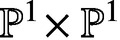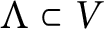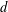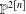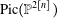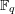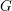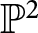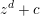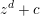Refine listing
Actions for selected content:
294 results in 14Hxx
ON THE FIRST STEPS OF THE MINIMAL MODEL PROGRAM FOR THE MODULI SPACE OF STABLE POINTED CURVES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 1 / January 2023
- Published online by Cambridge University Press:
- 22 April 2021, pp. 145-211
- Print publication:
- January 2023
-
- Article
-
- You have access
- Open access
- Export citation
Perverse Leray filtration and specialisation with applications to the Hitchin morphism
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 20 April 2021, pp. 443-487
- Print publication:
- March 2022
-
- Article
- Export citation
Pencils on Surfaces with Normal Crossings and the Kodaira Dimension of
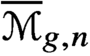 $\overline {\mathcal {M}}_{g,n}$
$\overline {\mathcal {M}}_{g,n}$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 12 April 2021, e31
-
- Article
-
- You have access
- Open access
- Export citation
A support theorem for Hilbert schemes of planar curves, II
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 4 / April 2021
- Published online by Cambridge University Press:
- 28 April 2021, pp. 835-882
- Print publication:
- April 2021
-
- Article
- Export citation
RANDOM REAL BRANCHED COVERINGS OF THE PROJECTIVE LINE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 09 February 2021, pp. 1783-1799
- Print publication:
- September 2022
-
- Article
- Export citation
Maps from Feigin and Odesskii's elliptic algebras to twisted homogeneous coordinate rings
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 11 January 2021, e4
-
- Article
-
- You have access
- Open access
- Export citation
RECURSION FOR MASUR-VEECH VOLUMES OF MODULI SPACES OF QUADRATIC DIFFERENTIALS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 4 / July 2022
- Published online by Cambridge University Press:
- 08 January 2021, pp. 1471-1476
- Print publication:
- July 2022
-
- Article
- Export citation
Brill-Noether theory for curves of a fixed gonality
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 9 / 2021
- Published online by Cambridge University Press:
- 08 January 2021, e1
-
- Article
-
- You have access
- Open access
- Export citation
Brill-Noether generality of binary curves
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 13 October 2020, pp. 787-807
- Print publication:
- December 2021
-
- Article
- Export citation
SPACE OF INITIAL VALUES OF A MAP WITH A QUARTIC INVARIANT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 05 October 2020, pp. 438-449
- Print publication:
- June 2021
-
- Article
- Export citation
K3 surfaces with involution, equivariant analytic torsion, and automorphic forms on the moduli space IV: The structure of the invariant
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 10 / October 2020
- Published online by Cambridge University Press:
- 19 November 2020, pp. 1965-2019
- Print publication:
- October 2020
-
- Article
- Export citation
G-torseurs en théorie de Hodge p-adique
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 10 / October 2020
- Published online by Cambridge University Press:
- 24 November 2020, pp. 2076-2110
- Print publication:
- October 2020
-
- Article
- Export citation
Criteria for periodicity and an application to elliptic functions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 14 August 2020, pp. 530-540
- Print publication:
- September 2021
-
- Article
- Export citation
Dynamical invariants of monomial correspondences
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 7 / July 2021
- Published online by Cambridge University Press:
- 02 June 2020, pp. 2000-2015
- Print publication:
- July 2021
-
- Article
- Export citation
ON THE POSITION OF NODES OF PLANE CURVES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 01 June 2020, pp. 62-68
- Print publication:
- February 2021
-
- Article
- Export citation
Cuspidal cohomology of stacks of shtukas
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 6 / June 2020
- Published online by Cambridge University Press:
- 14 May 2020, pp. 1079-1151
- Print publication:
- June 2020
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A Complete Classification of 3-dimensional Quadratic AS-regular Algebras of Type EC
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 27 April 2020, pp. 123-141
- Print publication:
- March 2021
-
- Article
- Export citation
Principal co-Higgs bundles on ℙ1
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 2 / May 2020
- Published online by Cambridge University Press:
- 05 March 2020, pp. 512-530
-
- Article
- Export citation
Gonality of dynatomic curves and strong uniform boundedness of preperiodic points
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 4 / April 2020
- Published online by Cambridge University Press:
- 17 February 2020, pp. 733-743
- Print publication:
- April 2020
-
- Article
- Export citation
Generalized Beilinson Elements and Generalized Soulé Characters
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 73 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 06 February 2020, pp. 542-571
- Print publication:
- April 2021
-
- Article
- Export citation