No CrossRef data available.
Article contents
Brill-Noether generality of binary curves
Published online by Cambridge University Press: 13 October 2020
Abstract
We show that the space 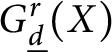 $G^r_{\underline d}(X)$ of linear series of certain multi-degree
$G^r_{\underline d}(X)$ of linear series of certain multi-degree 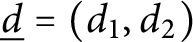 $\underline d=(d_1,d_2)$ (including the balanced ones) and rank r on a general genus-g binary curve X has dimension
$\underline d=(d_1,d_2)$ (including the balanced ones) and rank r on a general genus-g binary curve X has dimension 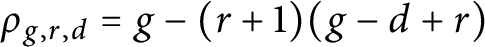 $\rho _{g,r,d}=g-(r+1)(g-d+r)$ if nonempty, where
$\rho _{g,r,d}=g-(r+1)(g-d+r)$ if nonempty, where 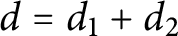 $d=d_1+d_2$. This generalizes Caporaso’s result from the case
$d=d_1+d_2$. This generalizes Caporaso’s result from the case 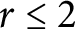 $r\leq 2$ to arbitrary rank, and shows that the space of Osserman-limit linear series on a general binary curve has the expected dimension, which was known for
$r\leq 2$ to arbitrary rank, and shows that the space of Osserman-limit linear series on a general binary curve has the expected dimension, which was known for 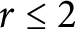 $r\leq 2$. In addition, we show that the space
$r\leq 2$. In addition, we show that the space 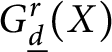 $G^r_{\underline d}(X)$ is still of expected dimension after imposing certain ramification conditions with respect to a sequence of increasing effective divisors supported on two general points
$G^r_{\underline d}(X)$ is still of expected dimension after imposing certain ramification conditions with respect to a sequence of increasing effective divisors supported on two general points 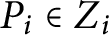 $P_i\in Z_i$, where
$P_i\in Z_i$, where 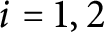 $i=1,2$ and
$i=1,2$ and 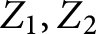 $Z_1,Z_2$ are the two components of X. Our result also has potential application to the lifting problem of divisors on graphs to divisors on algebraic curves.
$Z_1,Z_2$ are the two components of X. Our result also has potential application to the lifting problem of divisors on graphs to divisors on algebraic curves.
MSC classification
Information
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2020


