No CrossRef data available.
Article contents
RANDOM REAL BRANCHED COVERINGS OF THE PROJECTIVE LINE
Published online by Cambridge University Press: 09 February 2021
Abstract
In this paper, we construct a natural probability measure on the space of real branched coverings from a real projective algebraic curve 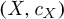 $(X,c_X)$ to the projective line
$(X,c_X)$ to the projective line 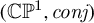 $(\mathbb{C} \mathbb {P}^1,\textit{conj} )$. We prove that the space of degree d real branched coverings having “many” real branched points (for example, more than
$(\mathbb{C} \mathbb {P}^1,\textit{conj} )$. We prove that the space of degree d real branched coverings having “many” real branched points (for example, more than 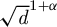 $\sqrt {d}^{1+\alpha }$, for any
$\sqrt {d}^{1+\alpha }$, for any 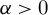 $\alpha>0$) has exponentially small measure. In particular, maximal real branched coverings – that is, real branched coverings such that all the branched points are real – are exponentially rare.
$\alpha>0$) has exponentially small measure. In particular, maximal real branched coverings – that is, real branched coverings such that all the branched points are real – are exponentially rare.
Information
- Type
- Research Article
- Information
- Journal of the Institute of Mathematics of Jussieu , Volume 21 , Issue 5 , September 2022 , pp. 1783 - 1799
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
Footnotes
The author is supported by the Israeli Science Foundation through ISF Grants 382/15 and 501/18
References
Ancona, M., Expected number and distribution of critical points of real Lefschetz pencils, Ann. Inst. Fourier (Grenoble), 70 (2020) no. 3 p. 1085–1113.Google Scholar
Ancona, M., Critical points of random branched coverings of the Riemann sphere, Math. Z. 296 (2020), 1735–1750.CrossRefGoogle Scholar
Berman, R., Berndtsson, B. and Sjöstrand, J., A direct approach to Bergman kernel asymptotics for positive line bundles, Ark. Mat. 46(2) (2008), 197–217.CrossRefGoogle Scholar
Dai, X., Liu, K. and Ma, X., On the asymptotic expansion of Bergman kernel, J. Differential Geom. 72(1) (2006), 1–41.CrossRefGoogle Scholar
Gayet, D. and Welschinger, J.-Y., Exponential rarefaction of real curves with many components, Publ. Math. Inst. Hautes Études Sci
. 113 (2011), 69–96.CrossRefGoogle Scholar
Gayet, D. and Welschinger, J.-Y., What is the total Betti number of a random real hypersurface?, J. Reine Angew. Math. 689 (2014), 137–168.Google Scholar
Gross, B. H. and Harris, J., Real algebraic curves, Ann. Sci. Éc. Norm. Supér. (4), 14(2) (1981), 157–182.CrossRefGoogle Scholar
Kostlan, E., On the distribution of roots of random polynomials, in From Topology to Computation: Proceedings of the Smalefest (Berkeley, CA, 1990), pp. 419–431 (Springer, New York, 1993).CrossRefGoogle Scholar
Ma, X. and Marinescu, G., Holomorphic Morse Inequalities and Bergman Kernels, Progress in Mathematics no. 254 (Birkhäuser Verlag, Basel, 2007).Google Scholar
Shiffman, B. and Zelditch, S., Distribution of zeros of random and quantum chaotic sections of positive line bundles, Comm. Math. Phys. 200(3) (1999), 661–683.CrossRefGoogle Scholar
Shub, M. and Smale, S., Complexity of Bezout’s theorem. II: Volumes and probabilities, in Computational Algebraic Geometry (Nice, 1992), Progress in Mathematics no. 109, pp. 267–285 (Birkhäuser Boston, Boston, 1993).Google Scholar
Tian, G., On a set of polarized Kähler metrics on algebraic manifolds, J. Differential Geom. 32(1) (1990), 99–130.Google Scholar
Zelditch, S., Szegö kernels and a theorem of Tian, Int. Math. Res. Not. IMRN 6 (1998), 317–331.CrossRefGoogle Scholar
Zelditch, S., Large deviations of empirical measures of zeros on Riemann surfaces, Int. Math. Res. Not. IMRN 3 (2013), 592–664.Google Scholar


