Article contents
JKL-ECM: an implementation of ECM using Hessian curves
Published online by Cambridge University Press: 26 August 2016
Abstract
We present JKL-ECM, an implementation of the elliptic curve method of integer factorization which uses certain twisted Hessian curves in a family studied by Jeon, Kim and Lee. This implementation takes advantage of torsion subgroup injection for families of elliptic curves over a quartic number field, in addition to the ‘small parameter’ speedup. We produced thousands of curves with torsion 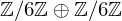 $\mathbb{Z}/6\mathbb{Z}\oplus \mathbb{Z}/6\mathbb{Z}$ and small parameters in twisted Hessian form, which admit curve arithmetic that is ‘almost’ as fast as that of twisted Edwards form. This allows JKL-ECM to compete with GMP-ECM for finding large prime factors. Also, JKL-ECM, based on GMP, accepts integers of arbitrary size. We classify the torsion subgroups of Hessian curves over
$\mathbb{Z}/6\mathbb{Z}\oplus \mathbb{Z}/6\mathbb{Z}$ and small parameters in twisted Hessian form, which admit curve arithmetic that is ‘almost’ as fast as that of twisted Edwards form. This allows JKL-ECM to compete with GMP-ECM for finding large prime factors. Also, JKL-ECM, based on GMP, accepts integers of arbitrary size. We classify the torsion subgroups of Hessian curves over 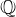 $\mathbb{Q}$ and further examine torsion properties of the curves described by Jeon, Kim and Lee. In addition, the high-performance curves with torsion
$\mathbb{Q}$ and further examine torsion properties of the curves described by Jeon, Kim and Lee. In addition, the high-performance curves with torsion 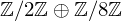 $\mathbb{Z}/2\mathbb{Z}\oplus \mathbb{Z}/8\mathbb{Z}$ of Bernstein et al. are completely recovered by the
$\mathbb{Z}/2\mathbb{Z}\oplus \mathbb{Z}/8\mathbb{Z}$ of Bernstein et al. are completely recovered by the 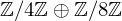 $\mathbb{Z}/4\mathbb{Z}\oplus \mathbb{Z}/8\mathbb{Z}$ family of Jeon, Kim and Lee, and hundreds more curves are produced besides, all with small parameters and base points.
$\mathbb{Z}/4\mathbb{Z}\oplus \mathbb{Z}/8\mathbb{Z}$ family of Jeon, Kim and Lee, and hundreds more curves are produced besides, all with small parameters and base points.
MSC classification
Information
- Type
- Research Article
- Information
- LMS Journal of Computation and Mathematics , Volume 19 , Special Issue A: Algorithmic Number Theory Symposium XII , 2016 , pp. 83 - 99
- Copyright
- © The Author(s) 2016
References
- 2
- Cited by

