Article contents
Second flip in the Hassett–Keel program: a local description
Published online by Cambridge University Press: 18 May 2017
Abstract
This is the first of three papers in which we give a moduli interpretation of the second flip in the log minimal model program for 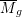 $\overline{M}_{g}$ , replacing the locus of curves with a genus
$\overline{M}_{g}$ , replacing the locus of curves with a genus 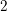 $2$ Weierstrass tail by a locus of curves with a ramphoid cusp. In this paper, for
$2$ Weierstrass tail by a locus of curves with a ramphoid cusp. In this paper, for 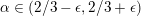 $\unicode[STIX]{x1D6FC}\in (2/3-\unicode[STIX]{x1D716},2/3+\unicode[STIX]{x1D716})$ , we introduce new
$\unicode[STIX]{x1D6FC}\in (2/3-\unicode[STIX]{x1D716},2/3+\unicode[STIX]{x1D716})$ , we introduce new 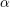 $\unicode[STIX]{x1D6FC}$ -stability conditions for curves and prove that they are deformation open. This yields algebraic stacks
$\unicode[STIX]{x1D6FC}$ -stability conditions for curves and prove that they are deformation open. This yields algebraic stacks 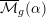 $\overline{{\mathcal{M}}}_{g}(\unicode[STIX]{x1D6FC})$ related by open immersions
$\overline{{\mathcal{M}}}_{g}(\unicode[STIX]{x1D6FC})$ related by open immersions 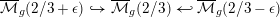 $\overline{{\mathcal{M}}}_{g}(2/3+\unicode[STIX]{x1D716}){\hookrightarrow}\overline{{\mathcal{M}}}_{g}(2/3){\hookleftarrow}\overline{{\mathcal{M}}}_{g}(2/3-\unicode[STIX]{x1D716})$ . We prove that around a curve
$\overline{{\mathcal{M}}}_{g}(2/3+\unicode[STIX]{x1D716}){\hookrightarrow}\overline{{\mathcal{M}}}_{g}(2/3){\hookleftarrow}\overline{{\mathcal{M}}}_{g}(2/3-\unicode[STIX]{x1D716})$ . We prove that around a curve  $C$ corresponding to a closed point in
$C$ corresponding to a closed point in 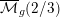 $\overline{{\mathcal{M}}}_{g}(2/3)$ , these open immersions are locally modeled by variation of geometric invariant theory for the action of
$\overline{{\mathcal{M}}}_{g}(2/3)$ , these open immersions are locally modeled by variation of geometric invariant theory for the action of 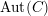 $\text{Aut}(C)$ on the first-order deformation space of
$\text{Aut}(C)$ on the first-order deformation space of 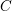 $C$ .
$C$ .
Keywords
Information
- Type
- Research Article
- Information
- Copyright
- © The Authors 2017
References
- 13
- Cited by

