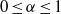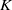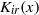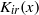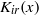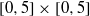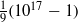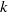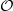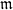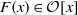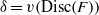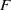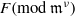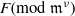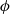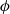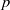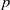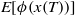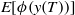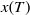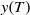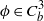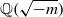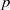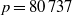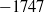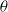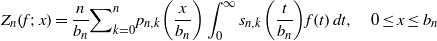Contents
Research Article
A comprehensive perturbation theorem for estimating magnitudes of roots of polynomials
-
- Published online by Cambridge University Press:
- 14 February 2013, pp. 1-8
-
- Article
-
- You have access
- Export citation
Computing zeta functions of nondegenerate hypersurfaces with few monomials
- Part of:
-
- Published online by Cambridge University Press:
- 14 February 2013, pp. 9-44
-
- Article
-
- You have access
- Export citation
On the continuity of multivariate Lagrange interpolation at natural lattices
- Part of:
-
- Published online by Cambridge University Press:
- 10 April 2013, pp. 45-60
-
- Article
-
- You have access
- Export citation
Complex B-splines and Hurwitz zeta functions
- Part of:
-
- Published online by Cambridge University Press:
- 10 April 2013, pp. 61-77
-
- Article
-
- You have access
- Export citation
Bounds and algorithms for the
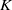 $K$ -Bessel function of imaginary order
$K$ -Bessel function of imaginary order
- Part of:
-
- Published online by Cambridge University Press:
- 10 April 2013, pp. 78-108
-
- Article
-
- You have access
- Export citation
Seven new champion linear codes
- Part of:
-
- Published online by Cambridge University Press:
- 01 January 2013, pp. 109-117
-
- Article
-
- You have access
- Export citation
Václav Šimerka: quadratic forms and factorization
- Part of:
-
- Published online by Cambridge University Press:
- 01 May 2013, pp. 118-129
-
- Article
-
- You have access
- Export citation
Minimal solvable nonic fields
- Part of:
-
- Published online by Cambridge University Press:
- 01 May 2013, pp. 130-138
-
- Article
-
- You have access
- Export citation
Complexity of OM factorizations of polynomials over local fields
- Part of:
-
- Published online by Cambridge University Press:
- 01 June 2013, pp. 139-171
-
- Article
-
- You have access
- Export citation
Single-class genera of positive integral lattices
- Part of:
-
- Published online by Cambridge University Press:
- 01 August 2013, pp. 172-186
-
- Article
-
- You have access
- Export citation
On level one cuspidal Bianchi modular forms
- Part of:
-
- Published online by Cambridge University Press:
- 01 August 2013, pp. 187-199
-
- Article
-
- You have access
- Export citation
Computing Borcherds products
- Part of:
-
- Published online by Cambridge University Press:
- 01 August 2013, pp. 200-215
-
- Article
-
- You have access
- Export citation
Explicit application of Waldspurger’s theorem
- Part of:
-
- Published online by Cambridge University Press:
- 01 August 2013, pp. 216-245
-
- Article
-
- You have access
- Export citation
Computing level one Hecke eigensystems (mod
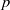 $p$ )
$p$ )
- Part of:
-
- Published online by Cambridge University Press:
- 01 August 2013, pp. 246-270
-
- Article
-
- You have access
- Export citation
Modular subgroups, dessins d’enfants and elliptic K3 surfaces
- Part of:
-
- Published online by Cambridge University Press:
- 01 August 2013, pp. 271-318
-
- Article
-
- You have access
- Export citation
Weak approximation of stochastic differential delay equations for bounded measurable function
- Part of:
-
- Published online by Cambridge University Press:
- 01 September 2013, pp. 319-343
-
- Article
-
- You have access
- Export citation
Higher torsion in the Abelianization of the full Bianchi groups
- Part of:
-
- Published online by Cambridge University Press:
- 01 September 2013, pp. 344-365
-
- Article
-
- You have access
- Export citation
Corrigenda
Corrigendum: On the use of a discrete form of the Itô formula in the article ‘Almost sure asymptotic stability analysis of the
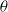 $\theta $ -Maruyama method applied to a test system with stabilising and destabilising stochastic perturbations’
$\theta $ -Maruyama method applied to a test system with stabilising and destabilising stochastic perturbations’
- Part of:
-
- Published online by Cambridge University Press:
- 01 September 2013, pp. 366-372
-
- Article
-
- You have access
- Export citation
Research Article
A vanishing theorem and symbolic powers of planar point ideals
- Part of:
-
- Published online by Cambridge University Press:
- 01 October 2013, pp. 373-387
-
- Article
-
- You have access
- Export citation
Approximation by a composition of Chlodowsky operators and Százs–Durrmeyer operators on weighted spaces
- Part of:
-
- Published online by Cambridge University Press:
- 01 October 2013, pp. 388-397
-
- Article
-
- You have access
- Export citation