Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Cano, Jennifer
Cheng, Meng
Mulligan, Michael
Nayak, Chetan
Plamadeala, Eugeniu
and
Yard, Jon
2014.
Bulk-edge correspondence in (2 + 1)-dimensional Abelian topological phases.
Physical Review B,
Vol. 89,
Issue. 11,
Kirschmer, Markus
2014.
One-class genera of maximal integral quadratic forms.
Journal of Number Theory,
Vol. 136,
Issue. ,
p.
375.
Berkovich, Alexander
and
Patane, Frank
2015.
Essentially Unique Representations by Certain Ternary Quadratic Forms.
Experimental Mathematics,
Vol. 24,
Issue. 1,
p.
8.
Earnest, A. G.
Kim, Ji Young
and
Meyer, N. D.
2015.
The strictly regular diagonal quaternary quadratic $$\mathbb Z$$ Z -lattices.
The Ramanujan Journal,
Vol. 37,
Issue. 3,
p.
563.
Kirschmer, Markus
and
Lorch, David
2016.
Ternary quadratic forms over number fields with small class number.
Journal of Number Theory,
Vol. 161,
Issue. ,
p.
343.
Kirschmer, Markus
and
Nebe, Gabriele
2017.
Algorithmic and Experimental Methods in Algebra, Geometry, and Number Theory.
p.
503.
Turkalj, Ivica
2018.
Reflective Lorentzian lattices of signature (5,1).
Journal of Algebra,
Vol. 513,
Issue. ,
p.
516.
Kirschmer, Markus
2019.
One-class genera of exceptional groups over number fields.
Journal de théorie des nombres de Bordeaux,
Vol. 30,
Issue. 3,
p.
847.
Smertnig, Daniel
and
Voight, John
2019.
Definite orders with locally free cancellation.
Transactions of the London Mathematical Society,
Vol. 6,
Issue. 1,
p.
53.
Kim, Kyoungmin
and
Oh, Byeong-Kweon
2020.
Quadratic forms with a strong regularity property on the representations of squares.
Journal of Number Theory,
Vol. 213,
Issue. ,
p.
254.
Mezzedimi, Giacomo
2021.
K3 Surfaces of zero entropy admitting an elliptic fibration with only irreducible fibers.
Journal of Algebra,
Vol. 587,
Issue. ,
p.
344.
Yu, Xun
2024.
K3 surface entropy and automorphism groups.
Journal of Algebraic Geometry,
Luo, Yifan
and
Zhou, Haigang
2025.
The classification and representations of positive definite ternary quadratic forms of level 4𝑁.
Mathematics of Computation,
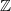 $ \mathbb{Z} $ -lattices in dimension
$ \mathbb{Z} $ -lattices in dimension 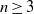 $n\geq 3$ whose genus consists of a single isometry class. This is achieved by using bounds obtained from the Smith–Minkowski–Siegel mass formula to computationally construct the square-free determinant lattices with this property, and then repeatedly calculating pre-images under a mapping first introduced by G. L. Watson.
$n\geq 3$ whose genus consists of a single isometry class. This is achieved by using bounds obtained from the Smith–Minkowski–Siegel mass formula to computationally construct the square-free determinant lattices with this property, and then repeatedly calculating pre-images under a mapping first introduced by G. L. Watson.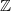 $ \mathbb{Z} $ -lattices has been compiled and incorporated into the Catalogue of Lattices.
$ \mathbb{Z} $ -lattices has been compiled and incorporated into the Catalogue of Lattices.
