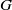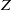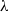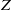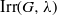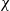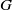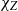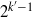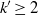Contents
Research Article
Computing characters of groups with central subgroups
- Part of:
-
- Published online by Cambridge University Press:
- 07 November 2013, pp. 398-406
-
- Article
-
- You have access
- Export citation
Singular values of multiple eta-quotients for ramified primes
- Part of:
-
- Published online by Cambridge University Press:
- 07 November 2013, pp. 407-418
-
- Article
-
- You have access
- Export citation
The minimal generating sets of
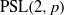 $\mathrm{PSL} (2, p)$ of size four
$\mathrm{PSL} (2, p)$ of size four
- Part of:
-
- Published online by Cambridge University Press:
- 06 November 2013, pp. 419-423
-
- Article
-
- You have access
- Export citation