No CrossRef data available.
Article contents
Computing characters of groups with central subgroups
Published online by Cambridge University Press: 07 November 2013
Abstract
The so-called Burnside–Dixon–Schneider (BDS) method, currently used as the default method of computing character tables in GAP for groups which are not solvable, is often inefficient in dealing with groups with large centres. If 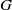 $G$ is a finite group with centre
$G$ is a finite group with centre 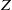 $Z$ and
$Z$ and 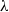 $\lambda $ a linear character of
$\lambda $ a linear character of 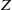 $Z$ , then we describe a method of computing the set
$Z$ , then we describe a method of computing the set 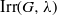 $\mathrm{Irr} (G, \lambda )$ of irreducible characters
$\mathrm{Irr} (G, \lambda )$ of irreducible characters 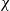 $\chi $ of
$\chi $ of 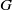 $G$ whose restriction
$G$ whose restriction 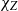 ${\chi }_{Z} $ is a multiple of
${\chi }_{Z} $ is a multiple of 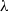 $\lambda $ . This modification of the BDS method involves only
$\lambda $ . This modification of the BDS method involves only 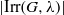 $\vert \mathrm{Irr} (G, \lambda )\vert $ conjugacy classes of
$\vert \mathrm{Irr} (G, \lambda )\vert $ conjugacy classes of 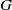 $G$ and so is relatively fast. A generalization of the method can be applied to computation of small sets of characters of groups with a solvable normal subgroup.
$G$ and so is relatively fast. A generalization of the method can be applied to computation of small sets of characters of groups with a solvable normal subgroup.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © The Author(s) 2013

