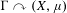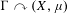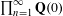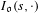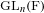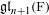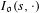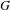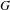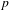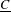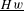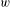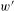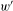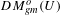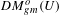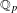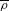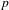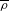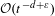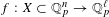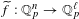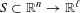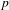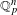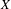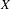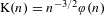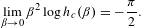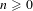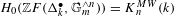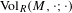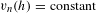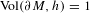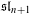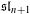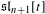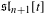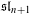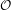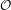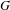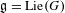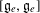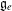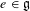Contents
Research Article
W-ALGEBRAS FROM HEISENBERG CATEGORIES
- Part of:
-
- Published online by Cambridge University Press:
- 13 July 2016, pp. 981-1017
-
- Article
- Export citation
POLISH MODELS AND SOFIC ENTROPY
- Part of:
-
- Published online by Cambridge University Press:
- 18 January 2016, pp. 241-275
-
- Article
- Export citation
ADJOINT FUNCTORS ON THE DERIVED CATEGORYOF MOTIVES
- Part of:
-
- Published online by Cambridge University Press:
- 22 March 2016, pp. 489-507
-
- Article
-
- You have access
- Export citation
LA VARIANTE INFINITÉSIMALE DE LA FORMULE DES TRACES DE JACQUET-RALLIS POUR LES GROUPES LINÉAIRES
-
- Published online by Cambridge University Press:
- 19 April 2016, pp. 735-783
-
- Article
- Export citation
FROM THE FUNCTION-SHEAF DICTIONARY TO QUASICHARACTERS OF
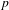 $p$ -ADIC TORI
$p$ -ADIC TORI
- Part of:
-
- Published online by Cambridge University Press:
- 13 October 2015, pp. 1-37
-
- Article
- Export citation
NON-COMMUTATIVE LOCALIZATIONS OF ADDITIVE CATEGORIES AND WEIGHT STRUCTURES
- Part of:
-
- Published online by Cambridge University Press:
- 24 May 2016, pp. 785-821
-
- Article
- Export citation
VARIÉTÉS DE KISIN STRATIFIÉES ET DÉFORMATIONS POTENTIELLEMENT BARSOTTI-TATE
-
- Published online by Cambridge University Press:
- 08 September 2016, pp. 1019-1064
-
- Article
- Export citation
LOCAL DECAY FOR THE DAMPED WAVE EQUATION IN THE ENERGY SPACE
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2016, pp. 509-540
-
- Article
- Export citation
A DEFINABLE
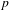 $p$ -ADIC ANALOGUE OF KIRSZBRAUN’S THEOREM ON EXTENSIONS OF LIPSCHITZ MAPS
$p$ -ADIC ANALOGUE OF KIRSZBRAUN’S THEOREM ON EXTENSIONS OF LIPSCHITZ MAPS
- Part of:
-
- Published online by Cambridge University Press:
- 20 October 2015, pp. 39-57
-
- Article
- Export citation
IMAGES OF QUANTUM REPRESENTATIONS OF MAPPING CLASS GROUPS AND DUPONT–GUICHARDET–WIGNER QUASI-HOMOMORPHISMS
- Part of:
-
- Published online by Cambridge University Press:
- 27 January 2016, pp. 277-304
-
- Article
- Export citation
PINNING ON A DEFECT LINE: CHARACTERIZATION OF MARGINAL DISORDER RELEVANCE AND SHARP ASYMPTOTICS FOR THE CRITICAL POINT SHIFT
- Part of:
-
- Published online by Cambridge University Press:
- 29 January 2016, pp. 305-346
-
- Article
- Export citation
SUPERORBITS
- Part of:
-
- Published online by Cambridge University Press:
- 20 July 2016, pp. 1065-1120
-
- Article
- Export citation
FRAMED CORRESPONDENCES AND THE MILNOR–WITT
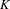 $K$-THEORY
$K$-THEORY
- Part of:
-
- Published online by Cambridge University Press:
- 30 June 2016, pp. 823-852
-
- Article
- Export citation
TRUNCATED BARSOTTI–TATE GROUPS AND DISPLAYS
- Part of:
-
- Published online by Cambridge University Press:
- 04 April 2016, pp. 541-581
-
- Article
- Export citation
PERIODS OF AUTOMORPHIC FORMS: THE TRILINEAR CASE
- Part of:
-
- Published online by Cambridge University Press:
- 26 October 2015, pp. 59-74
-
- Article
- Export citation
THE RENORMALIZED VOLUME AND UNIFORMIZATION OF CONFORMAL STRUCTURES
- Part of:
-
- Published online by Cambridge University Press:
- 30 June 2016, pp. 853-912
-
- Article
- Export citation
DEMAZURE MODULES OF LEVEL TWO AND PRIME REPRESENTATIONS OF QUANTUM AFFINE
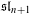 $\mathfrak{sl}_{n+1}$
$\mathfrak{sl}_{n+1}$
- Part of:
-
- Published online by Cambridge University Press:
- 09 November 2015, pp. 75-105
-
- Article
-
- You have access
- Export citation
PERVERSE MOTIVES AND GRADED DERIVED CATEGORY
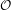 ${\mathcal{O}}$
${\mathcal{O}}$
- Part of:
-
- Published online by Cambridge University Press:
- 26 February 2016, pp. 347-395
-
- Article
- Export citation
INHOMOGENEOUS INCOMPRESSIBLE VISCOUS FLOWS WITH SLOWLY VARYING INITIAL DATA
- Part of:
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 1121-1172
-
- Article
- Export citation
RIGID ORBITS AND SHEETS IN REDUCTIVE LIE ALGEBRAS OVER FIELDS OF PRIME CHARACTERISTIC
- Part of:
-
- Published online by Cambridge University Press:
- 04 April 2016, pp. 583-613
-
- Article
- Export citation