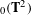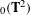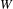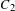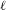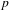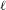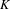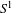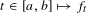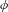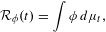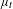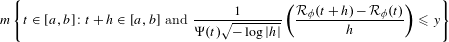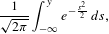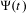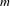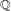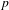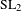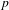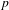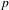Contents
Research Article
ON ANNULAR MAPS OF THE TORUS AND SUBLINEAR DIFFUSION
- Part of:
-
- Published online by Cambridge University Press:
- 23 June 2016, pp. 913-978
-
- Article
- Export citation
ON THE SQUARE-FREE REPRESENTATION FUNCTION OF A NORM FORM AND NILSEQUENCES
- Part of:
-
- Published online by Cambridge University Press:
- 11 November 2015, pp. 107-135
-
- Article
- Export citation
THE MODULI SPACE OF TWISTED CANONICAL DIVISORS
- Part of:
-
- Published online by Cambridge University Press:
- 05 April 2016, pp. 615-672
-
- Article
-
- You have access
- Export citation
COMPACT SPACES OF THE FIRST BAIRE CLASS THAT HAVE OPEN FINITE DEGREE
- Part of:
-
- Published online by Cambridge University Press:
- 21 November 2016, pp. 1173-1196
-
- Article
- Export citation
JOSEPH IDEALS AND LISSE MINIMAL
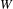 $W$ -ALGEBRAS
$W$ -ALGEBRAS
- Part of:
-
- Published online by Cambridge University Press:
- 07 March 2016, pp. 397-417
-
- Article
- Export citation
ON THE
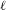 $\ell$-ADIC COHOMOLOGY OF SOME
$\ell$-ADIC COHOMOLOGY OF SOME 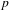 $p$-ADICALLY UNIFORMIZED SHIMURA VARIETIES
$p$-ADICALLY UNIFORMIZED SHIMURA VARIETIES
- Part of:
-
- Published online by Cambridge University Press:
- 01 December 2016, pp. 1197-1226
-
- Article
- Export citation
Corrigendum
TEST IDEALS IN RINGS WITH FINITELY GENERATED ANTI-CANONICAL ALGEBRAS – CORRIGENDUM
-
- Published online by Cambridge University Press:
- 04 August 2016, pp. 979-980
-
- Article
-
- You have access
- Export citation
Research Article
ON THE MOTIVIC SPECTRAL SEQUENCE
- Part of:
-
- Published online by Cambridge University Press:
- 25 November 2015, pp. 137-170
-
- Article
- Export citation
SUPERFICIAL FIBRES OF GENERIC PROJECTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 08 March 2016, pp. 419-424
-
- Article
- Export citation
CENTRAL LIMIT THEOREM FOR THE MODULUS OF CONTINUITY OF AVERAGES OF OBSERVABLES ON TRANSVERSAL FAMILIES OF PIECEWISE EXPANDING UNIMODAL MAPS
- Part of:
-
- Published online by Cambridge University Press:
- 13 July 2016, pp. 673-733
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
JMJ volume 17 Issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 23 April 2018, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Research Article
TEST IDEALS IN RINGS WITH FINITELY GENERATED ANTI-CANONICAL ALGEBRAS
- Part of:
-
- Published online by Cambridge University Press:
- 13 January 2016, pp. 171-206
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
JMJ volume 17 Issue 4 Cover and Front matter
-
- Published online by Cambridge University Press:
- 02 August 2018, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Research Article
 $L$ -INDISTINGUISHABILITY ON EIGENVARIETIES
$L$ -INDISTINGUISHABILITY ON EIGENVARIETIES
- Part of:
-
- Published online by Cambridge University Press:
- 22 March 2016, pp. 425-440
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
JMJ volume 17 Issue 5 Cover and Front matter
-
- Published online by Cambridge University Press:
- 03 October 2018, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
JMJ volume 17 Issue 5 Cover and Back matter
-
- Published online by Cambridge University Press:
- 03 October 2018, pp. b1-b4
-
- Article
-
- You have access
- Export citation
Research Article
SOLVABLE LIE GROUPS DEFINABLE IN O-MINIMAL THEORIES
- Part of:
-
- Published online by Cambridge University Press:
- 28 April 2016, pp. 441-452
-
- Article
- Export citation
Back Cover (OBC, IBC) and matter
JMJ volume 17 Issue 4 Cover and Back matter
-
- Published online by Cambridge University Press:
- 02 August 2018, pp. b1-b4
-
- Article
-
- You have access
- Export citation
Research Article
ON THE EXCEPTIONAL SPECIALIZATIONS OF BIG HEEGNER POINTS
- Part of:
-
- Published online by Cambridge University Press:
- 04 February 2016, pp. 207-240
-
- Article
- Export citation
Back Cover (OBC, IBC) and matter
JMJ volume 17 Issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 23 April 2018, pp. b1-b5
-
- Article
-
- You have access
- Export citation