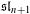 $\mathfrak{sl}_{n+1}$
$\mathfrak{sl}_{n+1}$Published online by Cambridge University Press: 09 November 2015
We study the classical limit of a family of irreducible representations of the quantum affine algebra associated to 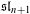 $\mathfrak{sl}_{n+1}$. After a suitable twist, the limit is a module for
$\mathfrak{sl}_{n+1}$. After a suitable twist, the limit is a module for 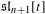 $\mathfrak{sl}_{n+1}[t]$, i.e., for the maximal standard parabolic subalgebra of the affine Lie algebra. Our first result is about the family of prime representations introduced in Hernandez and Leclerc (Duke Math. J.154 (2010), 265–341; Symmetries, Integrable Systems and Representations, Springer Proceedings in Mathematics & Statitics, Volume 40, pp. 175–193 (2013)), in the context of a monoidal categorification of cluster algebras. We show that these representations specialize (after twisting) to
$\mathfrak{sl}_{n+1}[t]$, i.e., for the maximal standard parabolic subalgebra of the affine Lie algebra. Our first result is about the family of prime representations introduced in Hernandez and Leclerc (Duke Math. J.154 (2010), 265–341; Symmetries, Integrable Systems and Representations, Springer Proceedings in Mathematics & Statitics, Volume 40, pp. 175–193 (2013)), in the context of a monoidal categorification of cluster algebras. We show that these representations specialize (after twisting) to 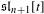 $\mathfrak{sl}_{n+1}[t]$-stable prime Demazure modules in level-two integrable highest-weight representations of the classical affine Lie algebra. It was proved in Chari et al. (arXiv:1408.4090) that a stable Demazure module is isomorphic to the fusion product of stable prime Demazure modules. Our next result proves that such a fusion product is the limit of the tensor product of the corresponding irreducible prime representations of quantum affine
$\mathfrak{sl}_{n+1}[t]$-stable prime Demazure modules in level-two integrable highest-weight representations of the classical affine Lie algebra. It was proved in Chari et al. (arXiv:1408.4090) that a stable Demazure module is isomorphic to the fusion product of stable prime Demazure modules. Our next result proves that such a fusion product is the limit of the tensor product of the corresponding irreducible prime representations of quantum affine 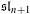 $\mathfrak{sl}_{n+1}$.
$\mathfrak{sl}_{n+1}$.