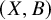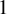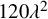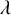Contents
Discrete Mathematics
Empty simplices of large width
- Part of:
-
- Published online by Cambridge University Press:
- 03 February 2025, e21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algebraic and Complex Geometry
Regenerations and applications
- Part of:
-
- Published online by Cambridge University Press:
- 03 February 2025, e22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Number Theory
Local newforms for generic representations of unramified even unitary groups I: Even conductor case
- Part of:
-
- Published online by Cambridge University Press:
- 03 February 2025, e23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Erratum
“The six-functor formalism for rigid analytic motives” – Erratum
- Part of:
-
- Published online by Cambridge University Press:
- 03 February 2025, e24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algebraic and Complex Geometry
A Torelli theorem for graphs via quasistable divisors
-
- Published online by Cambridge University Press:
- 03 February 2025, e25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algebra
Geometrization of the Satake transform for mod p Hecke algebras
- Part of:
-
- Published online by Cambridge University Press:
- 05 February 2025, e26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Research Article
Doubling constructions and tensor product L-functions: coverings of the symplectic group
- Part of:
-
- Published online by Cambridge University Press:
- 10 February 2025, e27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Discrete Mathematics
Quantum bumpless pipe dreams
- Part of:
-
- Published online by Cambridge University Press:
- 06 February 2025, e28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Analysis
Hyperbolic Metric Spaces and Stochastic Embeddings
- Part of:
-
- Published online by Cambridge University Press:
- 07 February 2025, e29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Computational Mathematics
Spectral Polyhedra
- Part of:
-
- Published online by Cambridge University Press:
- 06 February 2025, e30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Analysis
Complete positivity order and relative entropy decay
- Part of:
-
- Published online by Cambridge University Press:
- 06 February 2025, e31
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Probability
Measurable Vizing’s theorem
- Part of:
-
- Published online by Cambridge University Press:
- 07 February 2025, e32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algebra
A characterisation of higher torsion classes
- Part of:
-
- Published online by Cambridge University Press:
- 07 February 2025, e33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dynamics
Joint transitivity for linear iterates
- Part of:
-
- Published online by Cambridge University Press:
- 05 February 2025, e34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Topology
Graphing, homotopy groups of spheres, and spaces of long links and knots
- Part of:
-
- Published online by Cambridge University Press:
- 12 February 2025, e35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algebraic and Complex Geometry
Infinite flags and Schubert polynomials
- Part of:
-
- Published online by Cambridge University Press:
- 10 February 2025, e36
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Analysis
Higher Orbital Integrals, Cyclic Cocycles and Noncommutative Geometry
-
- Published online by Cambridge University Press:
- 10 February 2025, e37
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Discrete Mathematics
An efficient asymmetric removal lemma and its limitations
- Part of:
-
- Published online by Cambridge University Press:
- 10 February 2025, e38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Mathematical Physics
Complements and coregularity of Fano varieties
- Part of:
-
- Published online by Cambridge University Press:
- 07 February 2025, e39
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Number Theory
Average Analytic Ranks of Elliptic Curves over Number Fields
- Part of:
-
- Published online by Cambridge University Press:
- 11 February 2025, e40
-
- Article
-
- You have access
- Open access
- HTML
- Export citation