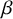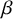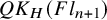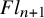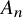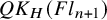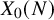Contents
Mathematical Physics
The extremal landscape for the C
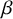 $\beta $E ensemble
$\beta $E ensemble
- Part of:
-
- Published online by Cambridge University Press:
- 13 January 2025, e1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algebraic and Complex Geometry
On families of K3 surfaces with real multiplication
- Part of:
-
- Published online by Cambridge University Press:
- 20 January 2025, e2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Topology
Free torus actions and twisted suspensions
- Part of:
-
- Published online by Cambridge University Press:
- 20 January 2025, e3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Discrete Mathematics
Rigidity of symmetric simplicial complexes and the lower bound theorem
- Part of:
-
- Published online by Cambridge University Press:
- 20 January 2025, e4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algebra
Closed approximate subgroups: compactness, amenability and approximate lattices
- Part of:
-
- Published online by Cambridge University Press:
- 20 January 2025, e5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Number Theory
A single source theorem for primitive points on curves
- Part of:
-
- Published online by Cambridge University Press:
- 20 January 2025, e6
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Discrete Mathematics
Bender–Knuth Billiards in Coxeter Groups
- Part of:
-
- Published online by Cambridge University Press:
- 24 January 2025, e7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algebra
Generic stabilizers for simple algebraic groups acting on orthogonal and symplectic Grassmannians
- Part of:
-
- Published online by Cambridge University Press:
- 24 January 2025, e8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algebraic and Complex Geometry
Equivariant geometry of singular cubic threefolds
- Part of:
-
- Published online by Cambridge University Press:
- 24 January 2025, e9
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Dynamics
Finding product sets in some classes of amenable groups
- Part of:
-
- Published online by Cambridge University Press:
- 24 January 2025, e10
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Analysis
Generalised Dirac-Schrödinger operators and the Callias Theorem
- Part of:
-
- Published online by Cambridge University Press:
- 24 January 2025, e11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Probability
Solution theory of fractional SDEs in complete subcritical regimes
- Part of:
-
- Published online by Cambridge University Press:
- 24 January 2025, e12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algebraic and Complex Geometry
Covering gonality of symmetric products of curves and Cayley–Bacharach condition on Grassmannians
- Part of:
-
- Published online by Cambridge University Press:
- 24 January 2025, e13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algebra
Abelian supplements in almost simple groups
- Part of:
-
- Published online by Cambridge University Press:
- 24 January 2025, e14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algebraic and Complex Geometry
A cone conjecture for log Calabi-Yau surfaces
- Part of:
-
- Published online by Cambridge University Press:
- 24 January 2025, e15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Erratum
Erratum to ‘From Curves to Currents’
- Part of:
-
- Published online by Cambridge University Press:
- 29 January 2025, e16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Probability
Large N limit of the Yang–Mills measure on compact surfaces II: Makeenko–Migdal equations and the planar master field
- Part of:
-
- Published online by Cambridge University Press:
- 28 January 2025, e17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algebraic and Complex Geometry
Canonical heights for abelian group actions of maximal dynamical rank
- Part of:
-
- Published online by Cambridge University Press:
- 28 January 2025, e18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algebra
A presentation of the torus-equivariant quantum K-theory ring of flag manifolds of type A, Part II: quantum double Grothendieck polynomials
- Part of:
-
- Published online by Cambridge University Press:
- 30 January 2025, e19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Number Theory
Complete verification of strong BSD for many modular abelian surfaces over
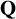 ${\mathbf {Q}}$
${\mathbf {Q}}$
- Part of:
-
- Published online by Cambridge University Press:
- 30 January 2025, e20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation