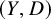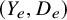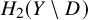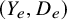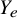1 Introduction
Given a smooth projective variety Y over
![]() $\mathbb {C}$
, the closed cone of curves of Y is the closure of the set of all nonnegative linear combinations of classes of irreducible curves in
$\mathbb {C}$
, the closed cone of curves of Y is the closure of the set of all nonnegative linear combinations of classes of irreducible curves in
![]() $H_{2}(Y, \mathbb {R})$
. The cone of curves of any Fano variety is rational polyhedral, meaning it has finitely many rational generators (see Theorem 1.24 on p.22 of [Reference Kollár and MoriKM98]). But this is not true in general for Calabi-Yau varieties – if Y is Calabi-Yau, the cone of curves of Y could be round, for example. The nef cone is the dual of the cone of curves.
$H_{2}(Y, \mathbb {R})$
. The cone of curves of any Fano variety is rational polyhedral, meaning it has finitely many rational generators (see Theorem 1.24 on p.22 of [Reference Kollár and MoriKM98]). But this is not true in general for Calabi-Yau varieties – if Y is Calabi-Yau, the cone of curves of Y could be round, for example. The nef cone is the dual of the cone of curves.
The Morrison cone conjecture states that if Y is a Calabi-Yau variety, then there exists a rational polyhedral cone which is a fundamental domain for the action of the automorphism group of Y on the nef cone. This can be pictured in dimension two using hyperbolic geometry (see, for example, [Reference TotaroT11]).
The conjecture is known to be true in dimension two, but for higher dimensions, it is an open question. In [Reference TotaroT10], Totaro has shown that a generalization of this conjecture is true in dimension two: if
![]() $(Y, \Delta )$
is a klt Calabi-Yau pair, then the automorphism group of Y acts on the nef cone with a rational polyhedral fundamental domain.
$(Y, \Delta )$
is a klt Calabi-Yau pair, then the automorphism group of Y acts on the nef cone with a rational polyhedral fundamental domain.
We study a cone conjecture for log Calabi-Yau surfaces that is similar to, but different from, the conjecture proved by Totaro (see Remark 1.3). Let Y be a smooth projective surface and D a reduced normal crossing divisor on Y such that
![]() $K_{Y} + D = 0$
. We call
$K_{Y} + D = 0$
. We call
![]() $(Y, D)$
a log Calabi-Yau surface. Additionally, we require D to be singular, and write
$(Y, D)$
a log Calabi-Yau surface. Additionally, we require D to be singular, and write
![]() $D = D_{1} + \dots + D_{n}$
for the irreducible components of D. By the Gross-Hacking-Keel Torelli theorem for log Calabi-Yau surfaces ([Reference Gross, Hacking and KeelGHK15b], Theorem 1.8), in each deformation type of log Calabi-Yau surfaces, there exists a unique pair
$D = D_{1} + \dots + D_{n}$
for the irreducible components of D. By the Gross-Hacking-Keel Torelli theorem for log Calabi-Yau surfaces ([Reference Gross, Hacking and KeelGHK15b], Theorem 1.8), in each deformation type of log Calabi-Yau surfaces, there exists a unique pair
![]() $(Y, D) = (Y_{e}, D_{e})$
such that the mixed Hodge structure on
$(Y, D) = (Y_{e}, D_{e})$
such that the mixed Hodge structure on
![]() $Y \setminus D$
is split. The main result of this paper is the proof of the following statement (see Theorem 5.1 and Theorem 5.2):
$Y \setminus D$
is split. The main result of this paper is the proof of the following statement (see Theorem 5.1 and Theorem 5.2):
Theorem 1.1. Consider a deformation type of log Calabi-Yau surfaces
![]() $(Y, D)$
with singular boundary.
$(Y, D)$
with singular boundary.
-
1. Let
 $(Y_{e}, D_{e})$
be the unique surface in this deformation type with split mixed Hodge structure. Let K be the kernel of the action of the automorphism group of the pair on
$(Y_{e}, D_{e})$
be the unique surface in this deformation type with split mixed Hodge structure. Let K be the kernel of the action of the automorphism group of the pair on
 $H^{2}(Y, \mathbb {Z})$
. Then
$H^{2}(Y, \mathbb {Z})$
. Then
 $\operatorname {\text {Aut}}(Y_{e}, D_{e})/K$
acts on the nef effective cone
$\operatorname {\text {Aut}}(Y_{e}, D_{e})/K$
acts on the nef effective cone
 $ {\operatorname {Nef}^{\; e}}(Y_{e})$
with a rational polyhedral fundamental domain.
$ {\operatorname {Nef}^{\; e}}(Y_{e})$
with a rational polyhedral fundamental domain. -
2. Let
 $(Y_{gen}, D_{gen})$
be a very general surface in this deformation type. Then the monodromy group
$(Y_{gen}, D_{gen})$
be a very general surface in this deformation type. Then the monodromy group
 $\operatorname {\text {Adm}}$
acts on the nef effective cone
$\operatorname {\text {Adm}}$
acts on the nef effective cone
 $ {\operatorname {Nef}^{\; e}}(Y_{gen})$
with a rational polyhedral fundamental domain.
$ {\operatorname {Nef}^{\; e}}(Y_{gen})$
with a rational polyhedral fundamental domain.
Remark 1.2. In (1) above, it is possible for
![]() $\operatorname {\text {Aut}}(Y_{e}, D_{e})$
to be infinite. For instance, consider when the negative definite or negative semidefinite boundary
$\operatorname {\text {Aut}}(Y_{e}, D_{e})$
to be infinite. For instance, consider when the negative definite or negative semidefinite boundary
![]() $D_{e}$
has
$D_{e}$
has
![]() $n=7$
components and suppose that D does not contain any
$n=7$
components and suppose that D does not contain any
![]() $(-1)$
-curves. Then
$(-1)$
-curves. Then
![]() $\operatorname {\text {Aut}}(Y_{e}, D_{e})$
is infinite (see Example 5.3 in [Reference Gross, Hacking and KeelGHK15b]). For
$\operatorname {\text {Aut}}(Y_{e}, D_{e})$
is infinite (see Example 5.3 in [Reference Gross, Hacking and KeelGHK15b]). For
![]() $n \leq 6$
, the group
$n \leq 6$
, the group
![]() $\operatorname {\text {Aut}}(Y_{e}, D_{e})$
is trivial (see Section 6).
$\operatorname {\text {Aut}}(Y_{e}, D_{e})$
is trivial (see Section 6).
The Morrison cone conjecture, stated in 1993, is originally inspired by mirror symmetry. The log Calabi-Yau surface version of this conjecture is also related to mirror symmetry through the deformation theory of cusp singularities of surfaces.
Given a log Calabi-Yau surface
![]() $(Y, D)$
such that the intersection matrix
$(Y, D)$
such that the intersection matrix
![]() $(D_{i} \cdot D_{j})$
is negative definite, we may contract the boundary D to obtain a normal surface Y with a cusp singularity
$(D_{i} \cdot D_{j})$
is negative definite, we may contract the boundary D to obtain a normal surface Y with a cusp singularity
![]() $p \in Y^{\prime }$
(see Grauert [Reference GrauertG62] and Definition 3.13). Cusp singularities come in dual pairs such that the links are diffeomorphic but have opposite orientations. If
$p \in Y^{\prime }$
(see Grauert [Reference GrauertG62] and Definition 3.13). Cusp singularities come in dual pairs such that the links are diffeomorphic but have opposite orientations. If
![]() $(Y^{\prime }, p)$
is obtained by contracting the boundary of a log Calabi-Yau surface
$(Y^{\prime }, p)$
is obtained by contracting the boundary of a log Calabi-Yau surface
![]() $(Y, D)$
to a cusp singularity
$(Y, D)$
to a cusp singularity
![]() $p \in Y^{\prime }$
, then, conjecturally,
$p \in Y^{\prime }$
, then, conjecturally,
![]() $(Y, D)$
corresponds to an irreducible component of the deformation space of the dual cusp ([Reference Gross, Hacking and KeelGHK15a], [Reference EngelE15], [Reference Engel and FriedmanEF16]). This is expected as a consequence of mirror symmetry:
$(Y, D)$
corresponds to an irreducible component of the deformation space of the dual cusp ([Reference Gross, Hacking and KeelGHK15a], [Reference EngelE15], [Reference Engel and FriedmanEF16]). This is expected as a consequence of mirror symmetry:
![]() $Y \backslash D$
is mirror to the Milnor fiber of the corresponding smoothing of the dual cusp ([Reference KeatingKe15], [Reference Hacking and KeatingHKe21]). Again conjecturally, the component of the deformation space of the dual cusp can be described in terms of the action of the monodromy group
$Y \backslash D$
is mirror to the Milnor fiber of the corresponding smoothing of the dual cusp ([Reference KeatingKe15], [Reference Hacking and KeatingHKe21]). Again conjecturally, the component of the deformation space of the dual cusp can be described in terms of the action of the monodromy group
![]() $\operatorname {\text {Adm}}$
on
$\operatorname {\text {Adm}}$
on
![]() $\operatorname {Nef}(Y^{\prime })$
, by a construction of Looijenga ([Reference LooijengaL03],
$\operatorname {Nef}(Y^{\prime })$
, by a construction of Looijenga ([Reference LooijengaL03],
![]() $\S 4$
). However, to use this construction, the group
$\S 4$
). However, to use this construction, the group
![]() $\operatorname {\text {Adm}}$
must act with a rational polyhedral fundamental domain on the effective nef cone of
$\operatorname {\text {Adm}}$
must act with a rational polyhedral fundamental domain on the effective nef cone of
![]() $Y^{\prime }$
, and this is the original motivation for our conjecture, cf. [Reference MorrisonM93].
$Y^{\prime }$
, and this is the original motivation for our conjecture, cf. [Reference MorrisonM93].
Remark 1.3 (A brief remark on some differences from Totaro’s work in [Reference TotaroT10]).
Totaro considers klt log Calabi-Yau pairs
![]() $(Y, \Delta )$
of dimension two, meaning that Y is a normal projective surface and
$(Y, \Delta )$
of dimension two, meaning that Y is a normal projective surface and
![]() $\Delta \subset Y$
is an effective
$\Delta \subset Y$
is an effective
![]() $\mathbb {Q}$
-divisor such that
$\mathbb {Q}$
-divisor such that
![]() $K_{Y} + \Delta $
is numerically equivalent to zero. Totaro proved the following theorem:
$K_{Y} + \Delta $
is numerically equivalent to zero. Totaro proved the following theorem:
Theorem 1.4 (Totaro).
Let
![]() $(Y, \Delta )$
be a klt log Calabi-Yau surface with
$(Y, \Delta )$
be a klt log Calabi-Yau surface with
![]() $K_{Y} + \Delta $
numerically equivalent to zero. Then the automorphism group of
$K_{Y} + \Delta $
numerically equivalent to zero. Then the automorphism group of
![]() $(Y, \Delta )$
acts on
$(Y, \Delta )$
acts on
![]() $ {\operatorname {Nef}^{\; e}}(Y)$
with a rational polyhedral fundamental domain.
$ {\operatorname {Nef}^{\; e}}(Y)$
with a rational polyhedral fundamental domain.
Suppose
![]() $(Y, \Delta )$
is a klt log Calabi-Yau pair and that
$(Y, \Delta )$
is a klt log Calabi-Yau pair and that
![]() $\Delta $
is contractible. Then there exists a birational morphism
$\Delta $
is contractible. Then there exists a birational morphism
![]() $Y \rightarrow Y^{\prime }$
where
$Y \rightarrow Y^{\prime }$
where
![]() $Y^{\prime }$
is a normal surface and
$Y^{\prime }$
is a normal surface and
![]() $\operatorname {\text {Supp}}(\Delta )$
is the exceptional locus. This the case where the intersection matrix of the components of
$\operatorname {\text {Supp}}(\Delta )$
is the exceptional locus. This the case where the intersection matrix of the components of
![]() $\Delta $
is negative definite, or equivalently, where the Iitaka dimension of
$\Delta $
is negative definite, or equivalently, where the Iitaka dimension of
![]() $-K_{Y}$
is zero. We note that the negative definite case is the essential case – the other possibilities are when the Iitaka dimension is one or two, the former reducing to Mori’s cone theorem, and the latter to the study of the Mordell-Weil group of an elliptic fibration. The resulting surface
$-K_{Y}$
is zero. We note that the negative definite case is the essential case – the other possibilities are when the Iitaka dimension is one or two, the former reducing to Mori’s cone theorem, and the latter to the study of the Mordell-Weil group of an elliptic fibration. The resulting surface
![]() $Y^{\prime }$
has log terminal singularities, and
$Y^{\prime }$
has log terminal singularities, and
![]() $K_{Y^{\prime }}$
is numerically equivalent to zero. There exists some
$K_{Y^{\prime }}$
is numerically equivalent to zero. There exists some
![]() $N \in \mathbb {N}$
such that
$N \in \mathbb {N}$
such that
![]() $NK_{Y^{\prime }}$
is linearly equivalent to zero, and we choose the minimal such N. Then there exists a finite morphism
$NK_{Y^{\prime }}$
is linearly equivalent to zero, and we choose the minimal such N. Then there exists a finite morphism
![]() $Z \rightarrow Y^{\prime }$
(the canonical covering), which is a
$Z \rightarrow Y^{\prime }$
(the canonical covering), which is a
![]() $\mathbb {Z}/N\mathbb {Z}$
covering where
$\mathbb {Z}/N\mathbb {Z}$
covering where
![]() $K_{Z}$
is linearly equivalent to zero and Z has canonical singularities. The minimal resolution
$K_{Z}$
is linearly equivalent to zero and Z has canonical singularities. The minimal resolution
![]() $\tilde {Z}$
of Z has
$\tilde {Z}$
of Z has
![]() $K_{\tilde {Z}}$
linearly equivalent to zero, and by classification of surfaces, we conclude that
$K_{\tilde {Z}}$
linearly equivalent to zero, and by classification of surfaces, we conclude that
![]() $\tilde {Z}$
is either a
$\tilde {Z}$
is either a
![]() $K3$
surface or an Abelian surface (and thus, the rank of
$K3$
surface or an Abelian surface (and thus, the rank of
![]() $\operatorname {Pic}(Y^{\prime })$
cannot exceed 20). Theorem 1.4 holds for
$\operatorname {Pic}(Y^{\prime })$
cannot exceed 20). Theorem 1.4 holds for
![]() $Y^{\prime }$
by the cone conjecture for
$Y^{\prime }$
by the cone conjecture for
![]() $K3$
and Abelian surfaces, and Totaro gives an argument ([Reference TotaroT10], p.257-259) showing that Theorem 1.4 holds for
$K3$
and Abelian surfaces, and Totaro gives an argument ([Reference TotaroT10], p.257-259) showing that Theorem 1.4 holds for
![]() $(Y, \Delta )$
.
$(Y, \Delta )$
.
In this paper, we consider a log Calabi-Yau surface
![]() $(Y, D)$
such that D is contractible: there exists a contraction
$(Y, D)$
such that D is contractible: there exists a contraction
![]() $Y \rightarrow Y^{\prime }$
, where
$Y \rightarrow Y^{\prime }$
, where
![]() $Y^{\prime }$
is a normal surface containing a cusp singularity p and
$Y^{\prime }$
is a normal surface containing a cusp singularity p and
![]() $K_{Y^{\prime }}$
is linearly equivalent to zero. Let
$K_{Y^{\prime }}$
is linearly equivalent to zero. Let
![]() $(Y_{e}, D_{e})$
be the distinguished pair in the deformation type of
$(Y_{e}, D_{e})$
be the distinguished pair in the deformation type of
![]() $(Y, D)$
with a split mixed Hodge structure. Then
$(Y, D)$
with a split mixed Hodge structure. Then
![]() $Y^{\prime }_{e}$
is projective. Moreover,
$Y^{\prime }_{e}$
is projective. Moreover,
![]() $\operatorname {Pic}(Y^{\prime }_{e})$
, which is identified via pullback with the orthogonal complement of the irreducible components of
$\operatorname {Pic}(Y^{\prime }_{e})$
, which is identified via pullback with the orthogonal complement of the irreducible components of
![]() $D_{e}$
in
$D_{e}$
in
![]() $\operatorname {Pic}(Y_{e})$
, has arbitrarily large rank. Theorem 1.1 (1) may be deduced from the analogous statement for
$\operatorname {Pic}(Y_{e})$
, has arbitrarily large rank. Theorem 1.1 (1) may be deduced from the analogous statement for
![]() $Y^{\prime }_{e}$
. However, the case of
$Y^{\prime }_{e}$
. However, the case of
![]() $Y^{\prime }_{e}$
is not related to the case of
$Y^{\prime }_{e}$
is not related to the case of
![]() $K3$
nor to the case of Abelian surfaces.
$K3$
nor to the case of Abelian surfaces.
Finally, we make a remark on the contribution to new examples. Looijenga studied the following: let L be a free Abelian group of finite rank and C an open convex cone in
![]() $V := L \otimes _{\mathbb {Z}} \mathbb {R}$
. Let
$V := L \otimes _{\mathbb {Z}} \mathbb {R}$
. Let
![]() $\Gamma $
be a group of automorphisms of L that preserve C, such that
$\Gamma $
be a group of automorphisms of L that preserve C, such that
![]() $\Gamma $
acts with a rational polyhedral fundamental domain on
$\Gamma $
acts with a rational polyhedral fundamental domain on
![]() $C_{+}:=\operatorname {\text {Conv}}(\bar {C} \cap L)$
. In this setting, Looijenga constructed a complex analytic compactification of the tube
$C_{+}:=\operatorname {\text {Conv}}(\bar {C} \cap L)$
. In this setting, Looijenga constructed a complex analytic compactification of the tube
![]() $(V+iC)/\Gamma $
. Some examples of such compactification include the cases where
$(V+iC)/\Gamma $
. Some examples of such compactification include the cases where
-
1. C is a homogeneous self-dual cone;
-
2. C is the Tits cone of a Coxeter group, which is not of finite nor of affine type; and
-
3. C is the nef or movable cone of a (log) Calabi-Yau variety for which the Morrison cone conjecture holds.
Theorem 1.1 contributes many new examples. In particular, some examples from Theorem 1.1 (2) (that is, when D has at most five components; see [Reference LooijengaL81]) are dual to Tits cones of Weyl groups, but this is not the case in general. Many known cases of the Morrison cone conjecture (e.g.,
![]() $K3$
surfaces [Reference SterkS85]; hyperkähler manifolds [Reference MarkmanM11], [Reference Markman and YoshiokaM15], [Reference Amerik and VerbitskyAV17]) are closely related to the homogeneous self-dual case via the description of the nef or movable cone in terms of a Coxeter group acting on a homogeneous self-dual cone (see, for example, [Reference Barth, Hulek, Peters and Van de VenBHPV04] and [Reference MarkmanM11]).
$K3$
surfaces [Reference SterkS85]; hyperkähler manifolds [Reference MarkmanM11], [Reference Markman and YoshiokaM15], [Reference Amerik and VerbitskyAV17]) are closely related to the homogeneous self-dual case via the description of the nef or movable cone in terms of a Coxeter group acting on a homogeneous self-dual cone (see, for example, [Reference Barth, Hulek, Peters and Van de VenBHPV04] and [Reference MarkmanM11]).
This paper is organized as follows. Section 2 contains the motivations of our project. Sections 3–5 contain the proof of the main theorem. In Section 6, we give explicit descriptions of certain cones of curves, which provide infinite series of new examples of Mori Dream Spaces. Here, I emphasize that this section considers cases
![]() $n \leq 6$
, where n is the length of the negative definite or negative semidefinite boundary D – these are specific cases of Theorem 5.4 described more precisely.
$n \leq 6$
, where n is the length of the negative definite or negative semidefinite boundary D – these are specific cases of Theorem 5.4 described more precisely.
2 Motivations
Let
![]() $(q \in X)$
be a cusp singularity. Cusp singularities come in dual pairs such that the links are diffeomorphic but have opposite orientations (cf. [Reference LooijengaL81], §III.2.1). There is the following conjecture (cf. [Reference EngelE15], Conjecture 6.2.5):
$(q \in X)$
be a cusp singularity. Cusp singularities come in dual pairs such that the links are diffeomorphic but have opposite orientations (cf. [Reference LooijengaL81], §III.2.1). There is the following conjecture (cf. [Reference EngelE15], Conjecture 6.2.5):
-
1. The smoothing components of the deformation space of
 $(q \in X)$
, up to isomorphism, are in bijective correspondence with deformation types of log Calabi-Yau surfaces
$(q \in X)$
, up to isomorphism, are in bijective correspondence with deformation types of log Calabi-Yau surfaces
 $(Y, D)$
such that D does not contain any
$(Y, D)$
such that D does not contain any
 $(-1)$
-curves and contracts to the dual cusp p.
$(-1)$
-curves and contracts to the dual cusp p. -
2. The smoothing component of
 $(q \in X)$
associated to
$(q \in X)$
associated to
 $(Y, D)$
is the Looijenga space determined by the action of
$(Y, D)$
is the Looijenga space determined by the action of
 $\operatorname {\text {Adm}}$
on the nef effective cone
$\operatorname {\text {Adm}}$
on the nef effective cone
 $ {\operatorname {Nef}^{\; e}}(Y^{\prime }_{gen})$
, which is contained in
$ {\operatorname {Nef}^{\; e}}(Y^{\prime }_{gen})$
, which is contained in
 $\langle D_{1}, \dots , D_{n} \rangle ^{\bot } \otimes _{\mathbb {Z}} \mathbb {R}$
. (Looijenga’s construction is described in [Reference LooijengaL03], Section
$\langle D_{1}, \dots , D_{n} \rangle ^{\bot } \otimes _{\mathbb {Z}} \mathbb {R}$
. (Looijenga’s construction is described in [Reference LooijengaL03], Section
 $4$
).
$4$
).
Looijenga’s construction requires that
![]() $\operatorname {\text {Adm}}$
acts on
$\operatorname {\text {Adm}}$
acts on
![]() $ {\operatorname {Nef}^{\; e}}(Y^{\prime }_{gen})$
with a rational polyhedral fundamental domain (Theorem 5.1), and this is one motivation for the cone conjecture for log Calabi-Yau surfaces. This is analogous to the original motivation for the Morrison cone conjecture for Calabi-Yau threefolds Y ([Reference MorrisonM93]): Morrison argues that the Looijenga space determined by the action of
$ {\operatorname {Nef}^{\; e}}(Y^{\prime }_{gen})$
with a rational polyhedral fundamental domain (Theorem 5.1), and this is one motivation for the cone conjecture for log Calabi-Yau surfaces. This is analogous to the original motivation for the Morrison cone conjecture for Calabi-Yau threefolds Y ([Reference MorrisonM93]): Morrison argues that the Looijenga space determined by the action of
![]() $\operatorname {\text {Aut}}(Y)$
on
$\operatorname {\text {Aut}}(Y)$
on
![]() $ {\operatorname {Nef}^{\; e}}(Y)$
is identified with a neighborhood of a boundary point of the moduli of the mirror of Y.
$ {\operatorname {Nef}^{\; e}}(Y)$
is identified with a neighborhood of a boundary point of the moduli of the mirror of Y.
The log Calabi-Yau cone conjecture can provide insight into the original Morrison cone conjecture because it includes more accessible cases. For instance, in every dimension, there are many log Calabi-Yau pairs
![]() $(Y, D)$
such that the variety Y is rational. In addition, the cone conjecture is related to the abundance conjecture ([Reference TotaroT11]), which is a long-standing open question of the minimal model program.
$(Y, D)$
such that the variety Y is rational. In addition, the cone conjecture is related to the abundance conjecture ([Reference TotaroT11]), which is a long-standing open question of the minimal model program.
Remark 2.1. The cone conjecture for log Calabi-Yau surfaces suggests that the Morrison cone conjecture is false in general, because it is the monodromy group
![]() $\operatorname {\text {Adm}}$
that acts with a rational polyhedral fundamental domain on
$\operatorname {\text {Adm}}$
that acts with a rational polyhedral fundamental domain on
![]() $ {\operatorname {Nef}^{\; e}}(Y_{gen})$
, and not the automorphism group.
$ {\operatorname {Nef}^{\; e}}(Y_{gen})$
, and not the automorphism group.
Remark 2.2. The explicit description of
![]() $\operatorname {Nef}(Y_{e})$
can be used to verify the conjecture (1) stated above. For
$\operatorname {Nef}(Y_{e})$
can be used to verify the conjecture (1) stated above. For
![]() $n \leq 5$
, this follows from work of Looijenga [Reference LooijengaL81], and for
$n \leq 5$
, this follows from work of Looijenga [Reference LooijengaL81], and for
![]() $n = 6$
, we expect that it can be verified using work of Brohme ([Reference BrohmeB95]). The deformation theory for
$n = 6$
, we expect that it can be verified using work of Brohme ([Reference BrohmeB95]). The deformation theory for
![]() $n> 6$
is not known.
$n> 6$
is not known.
3 Background
Let Y be a smooth projective variety. We define
![]() $N^{1}(Y)$
to be the space of divisors with real coefficients modulo numerical equivalence, and the space
$N^{1}(Y)$
to be the space of divisors with real coefficients modulo numerical equivalence, and the space
![]() $N_{1}(Y)$
to be the space of 1-cycles with real coefficients modulo numerical equivalence. Because Y is a rational surface in our setting,
$N_{1}(Y)$
to be the space of 1-cycles with real coefficients modulo numerical equivalence. Because Y is a rational surface in our setting,
and
![]() $N^{1}(Y) = N_{1}(Y)$
. We define the nef cone of Y to be
$N^{1}(Y) = N_{1}(Y)$
. We define the nef cone of Y to be
The effective cone of Y is
 $$ \begin{align*} \operatorname{Eff}(Y) = \bigg\{ {\sum} a_{i} [D_{i}] \in N^{1}(Y) \; \vert \; a_{i} \in \mathbb{R}_{\geq 0} \text{ and } D_{i} \subset Y \text{ are codimension one subvarieties} \bigg\}. \end{align*} $$
$$ \begin{align*} \operatorname{Eff}(Y) = \bigg\{ {\sum} a_{i} [D_{i}] \in N^{1}(Y) \; \vert \; a_{i} \in \mathbb{R}_{\geq 0} \text{ and } D_{i} \subset Y \text{ are codimension one subvarieties} \bigg\}. \end{align*} $$
Following Kawamata in [Reference KawamataK97], we define the nef effective cone of Y to be
We denote the convex hull of the set S by
![]() $\operatorname {\text {Conv}}(S)$
, where S is subset of a real vector space. If Y is a surface, then
$\operatorname {\text {Conv}}(S)$
, where S is subset of a real vector space. If Y is a surface, then
Definition 3.4. The cone of curves of Y is defined as follows:
We write
![]() $\operatorname { {\overline{Curv}}}(Y)$
to mean the closure of the cone of curves.
$\operatorname { {\overline{Curv}}}(Y)$
to mean the closure of the cone of curves.
Definition 3.5. Let L be a finitely generated free Abelian group (i.e.,
![]() $L \simeq \mathbb {Z}^{\rho }$
for some
$L \simeq \mathbb {Z}^{\rho }$
for some
![]() $\rho \geq 0$
). A cone
$\rho \geq 0$
). A cone
![]() $C \subset L \otimes _{\mathbb {Z}} \mathbb {R} \simeq \mathbb {R}^{\rho }$
is said to be rational polyhedral if
$C \subset L \otimes _{\mathbb {Z}} \mathbb {R} \simeq \mathbb {R}^{\rho }$
is said to be rational polyhedral if
for some
![]() $v_{1}, \dots , v_{r} \in L$
. That is, the cone C is generated by finitely many integral vectors
$v_{1}, \dots , v_{r} \in L$
. That is, the cone C is generated by finitely many integral vectors
![]() $v_{1}, \dots , v_{r} \in L$
.
$v_{1}, \dots , v_{r} \in L$
.
Definition 3.6. A log Calabi-Yau surface is a pair
![]() $(Y, D)$
where Y is a smooth complex projective surface and
$(Y, D)$
where Y is a smooth complex projective surface and
![]() $D \subset Y$
is a reduced normal crossing divisor such that
$D \subset Y$
is a reduced normal crossing divisor such that
![]() $K_{Y} + D = 0$
. We say that
$K_{Y} + D = 0$
. We say that
![]() $(Y, D)$
has maximal boundary if D is singular. We write
$(Y, D)$
has maximal boundary if D is singular. We write
![]() $D = D_{1} + \dots + D_{n}$
, where n is the number of irreducible components or the length of D.
$D = D_{1} + \dots + D_{n}$
, where n is the number of irreducible components or the length of D.
In this paper, we always assume that
![]() $(Y, D)$
has maximal boundary. If
$(Y, D)$
has maximal boundary. If
![]() $(Y, D)$
is a log Calabi-Yau surface with maximal boundary, then Y is a rational surface ([Reference Gross, Hacking and KeelGHK15b], p.2).
$(Y, D)$
is a log Calabi-Yau surface with maximal boundary, then Y is a rational surface ([Reference Gross, Hacking and KeelGHK15b], p.2).
Remark 3.7. The boundary D is either a rational curve of arithmetic genus one with a single node (i.e., a copy of
![]() $\mathbb {P}^{1}$
with two points identified to form a node), or it is a cycle of smooth rational curves (i.e., a cycle of n copies of
$\mathbb {P}^{1}$
with two points identified to form a node), or it is a cycle of smooth rational curves (i.e., a cycle of n copies of
![]() $\mathbb {P}^{1}$
). This follows from the adjunction formula. We fix a cyclic ordering
$\mathbb {P}^{1}$
). This follows from the adjunction formula. We fix a cyclic ordering
![]() $D = D_{1} + \dots + D_{n}$
of the components of D and a compatible orientation (an isomorphism
$D = D_{1} + \dots + D_{n}$
of the components of D and a compatible orientation (an isomorphism
![]() $H_{1}(D, \mathbb {Z}) \simeq \mathbb {Z})$
. This orientation is uniquely determined by the cyclic ordering for
$H_{1}(D, \mathbb {Z}) \simeq \mathbb {Z})$
. This orientation is uniquely determined by the cyclic ordering for
![]() $n> 2$
.
$n> 2$
.
Definition 3.8. We say that a log Calabi-Yau surface
![]() $(Y, D)$
is generic if there are no
$(Y, D)$
is generic if there are no
![]() $(-2)$
-curves C contained in
$(-2)$
-curves C contained in
![]() $Y \setminus D$
. We sometimes write
$Y \setminus D$
. We sometimes write
![]() $(Y_{gen}, D_{gen})$
to denote one such log Calabi-Yau surface in a given deformation type.
$(Y_{gen}, D_{gen})$
to denote one such log Calabi-Yau surface in a given deformation type.
Definition 3.9. Two log Calabi-Yau surfaces
![]() $(Y^{1}, D^{1})$
and
$(Y^{1}, D^{1})$
and
![]() $(Y^{2}, D^{2})$
are said to be deformation equivalent if there exists a flat family
$(Y^{2}, D^{2})$
are said to be deformation equivalent if there exists a flat family
![]() $(\mathcal {Y}, \mathcal {D}) = (\mathcal {Y}, \mathcal {D}_{1} + \cdots + \mathcal {D}_{n})$
of log Calabi-Yau surfaces over a connected base S such that there are points
$(\mathcal {Y}, \mathcal {D}) = (\mathcal {Y}, \mathcal {D}_{1} + \cdots + \mathcal {D}_{n})$
of log Calabi-Yau surfaces over a connected base S such that there are points
![]() $p, q \in S$
with fibers
$p, q \in S$
with fibers
![]() $f^{-1}(p) = (Y^{1}, D^{1})$
and
$f^{-1}(p) = (Y^{1}, D^{1})$
and
![]() $f^{-1}(q) = (Y^{2}, D^{2})$
. In this case, we say that
$f^{-1}(q) = (Y^{2}, D^{2})$
. In this case, we say that
![]() $(Y^{1}, D^{1})$
and
$(Y^{1}, D^{1})$
and
![]() $(Y^{2}, D^{2})$
are of the same deformation type.
$(Y^{2}, D^{2})$
are of the same deformation type.
By the Torelli Theorem in [Reference Gross, Hacking and KeelGHK15b], given a log Calabi-Yau surface
![]() $(Y, D)$
, the moduli space
$(Y, D)$
, the moduli space
![]() $\mathcal {M}$
of log Calabi-Yau surfaces that are deformation equivalent to
$\mathcal {M}$
of log Calabi-Yau surfaces that are deformation equivalent to
![]() $(Y, D)$
can be described explicitly, and the locus of generic surfaces is the complement of a countable union of divisors in
$(Y, D)$
can be described explicitly, and the locus of generic surfaces is the complement of a countable union of divisors in
![]() $\mathcal {M}$
(see [Reference Gross, Hacking and KeelGHK15b], Section 6). For any two generic surfaces of the same deformation type, the nef cones of the two surfaces are the same. This cone for
$\mathcal {M}$
(see [Reference Gross, Hacking and KeelGHK15b], Section 6). For any two generic surfaces of the same deformation type, the nef cones of the two surfaces are the same. This cone for
![]() $Y_{gen}$
is described after the following definition:
$Y_{gen}$
is described after the following definition:
Definition 3.10. For a log Calabi-Yau surface
![]() $(Y, D)$
, an interior
$(Y, D)$
, an interior
![]() $(-1)$
-curve is a smooth rational curve of self-intersection
$(-1)$
-curve is a smooth rational curve of self-intersection
![]() $-1$
that is not contained in the boundary D. By the adjunction formula, such a curve must intersect the boundary transversely at a single point.
$-1$
that is not contained in the boundary D. By the adjunction formula, such a curve must intersect the boundary transversely at a single point.
Proposition 3.11 ([Reference Gross, Hacking and KeelGHK15b], Lemma 2.15).
 $$ \begin{align*} \operatorname{Nef}(Y_{gen}) = \{ L \in \operatorname{Pic}(Y) \otimes_{\mathbb{Z}} \mathbb{R} \; \vert \; &L^{2} \geq 0 \text{ and } L \cdot D_{i} \geq 0 \; \text{ for all } \; i \text{ and } \\ &L \cdot C \geq 0 \; \text{ for any interior (-1)-curve } C\}. \end{align*} $$
$$ \begin{align*} \operatorname{Nef}(Y_{gen}) = \{ L \in \operatorname{Pic}(Y) \otimes_{\mathbb{Z}} \mathbb{R} \; \vert \; &L^{2} \geq 0 \text{ and } L \cdot D_{i} \geq 0 \; \text{ for all } \; i \text{ and } \\ &L \cdot C \geq 0 \; \text{ for any interior (-1)-curve } C\}. \end{align*} $$
Lemma 3.12. Let
![]() $(Y, D)$
be a log Calabi-Yau surface. If
$(Y, D)$
be a log Calabi-Yau surface. If
![]() $L \in \operatorname {Pic}(Y)$
is nef, then L is effective.
$L \in \operatorname {Pic}(Y)$
is nef, then L is effective.
Proof. Let
![]() $L \in \operatorname {Pic}(Y)$
be nef. By Riemann-Roch, we have
$L \in \operatorname {Pic}(Y)$
be nef. By Riemann-Roch, we have
 $$ \begin{align*} \chi(L) &= \chi(\mathcal{O}_{Y}) + \displaystyle{\frac{1}{2} L(L - K_{Y})} \\ &= 1 + \displaystyle{\frac{1}{2}(L^{2} + L \cdot D)} \\ &\geq 1, \end{align*} $$
$$ \begin{align*} \chi(L) &= \chi(\mathcal{O}_{Y}) + \displaystyle{\frac{1}{2} L(L - K_{Y})} \\ &= 1 + \displaystyle{\frac{1}{2}(L^{2} + L \cdot D)} \\ &\geq 1, \end{align*} $$
since L being nef and D being effective give
![]() $L \cdot D \geq 0$
and L nef gives
$L \cdot D \geq 0$
and L nef gives
![]() $L^{2} \geq 0$
. However, we have
$L^{2} \geq 0$
. However, we have
 $$ \begin{align*} \chi(L) &= h^{0}(L) - h^{1}(L) + h^{2}(L). \\ &\leq h^{0}(L) + h^{2}(L) \end{align*} $$
$$ \begin{align*} \chi(L) &= h^{0}(L) - h^{1}(L) + h^{2}(L). \\ &\leq h^{0}(L) + h^{2}(L) \end{align*} $$
Next, we show that
![]() $h^{2}(L) = 0$
. By Serre Duality, we have
$h^{2}(L) = 0$
. By Serre Duality, we have
![]() $h^{2}(L) = h^{0}(K_{Y} - L) = h^{0}(-D-L)$
. If H is ample and L is nef and D is effective, then we have
$h^{2}(L) = h^{0}(K_{Y} - L) = h^{0}(-D-L)$
. If H is ample and L is nef and D is effective, then we have
![]() $H \cdot D> 0$
and
$H \cdot D> 0$
and
![]() $H \cdot L \geq 0$
. Then
$H \cdot L \geq 0$
. Then
![]() $H \cdot (-D - L) < 0$
, so
$H \cdot (-D - L) < 0$
, so
![]() $h^{0}(-D-L) = 0$
. Thus,
$h^{0}(-D-L) = 0$
. Thus,
![]() $h^{0}(L) \geq \chi (L) \geq 1$
, and therefore, L is linearly equivalent to an effective divisor.
$h^{0}(L) \geq \chi (L) \geq 1$
, and therefore, L is linearly equivalent to an effective divisor.
Definition 3.13. A cusp singularity is a surface singularity whose minimal resolution is a cycle of smooth rational curves that meet transversally. That is, the exceptional locus of the minimal resolution of a cusp singularity is a union of copies of
![]() $\mathbb {P}^{1}$
with nodal singularities such that the dual graph is a cycle.
$\mathbb {P}^{1}$
with nodal singularities such that the dual graph is a cycle.
Given a log Calabi-Yau surface
![]() $(Y, D)$
with D having a negative definite intersection matrix
$(Y, D)$
with D having a negative definite intersection matrix
![]() $(D_{i} \cdot D_{j})$
, it is possible to contract D to a cusp singularity p (by a theorem of Grauert on the contractibility of a negative definite configuration of curves on a smooth complex surface in the analytic category, [Reference GrauertG62]). Let
$(D_{i} \cdot D_{j})$
, it is possible to contract D to a cusp singularity p (by a theorem of Grauert on the contractibility of a negative definite configuration of curves on a smooth complex surface in the analytic category, [Reference GrauertG62]). Let
![]() $f: Y \rightarrow Y^{\prime }$
be the morphism contracting D to a point. Then we have the induced isomorphism
$f: Y \rightarrow Y^{\prime }$
be the morphism contracting D to a point. Then we have the induced isomorphism
and
![]() $f^{-1}(p) = D$
. In addition, the surface
$f^{-1}(p) = D$
. In addition, the surface
![]() $Y^{\prime }$
is normal and compact (for the usual Euclidean topology). We note that although Y is a projective variety, the new surface
$Y^{\prime }$
is normal and compact (for the usual Euclidean topology). We note that although Y is a projective variety, the new surface
![]() $Y^{\prime }$
is in general no longer a projective variety, but a normal, analytic space. We make the following definitions.
$Y^{\prime }$
is in general no longer a projective variety, but a normal, analytic space. We make the following definitions.
Definition 3.14. We define the nef effective cone of
![]() $Y^{\prime }$
in the following way:
$Y^{\prime }$
in the following way:
Remark 3.15. Equivalently,
![]() $ {\operatorname {Nef}^{\; e}}(Y^{\prime }) = \operatorname {Nef}(Y^{\prime }) \cap \operatorname {Eff}(Y^{\prime })$
, where
$ {\operatorname {Nef}^{\; e}}(Y^{\prime }) = \operatorname {Nef}(Y^{\prime }) \cap \operatorname {Eff}(Y^{\prime })$
, where
and we use Mumford’s intersection product on a normal surface
![]() $Y^{\prime }$
([Reference MumfordM61], p.17). Note that
$Y^{\prime }$
([Reference MumfordM61], p.17). Note that
![]() $Y^{\prime }$
is not
$Y^{\prime }$
is not
![]() $\mathbb {Q}$
-factorial in general (i.e., there may exist divisors which are not
$\mathbb {Q}$
-factorial in general (i.e., there may exist divisors which are not
![]() $\mathbb {Q}$
-Cartier).
$\mathbb {Q}$
-Cartier).
Definition 3.16. An isomorphism of log Calabi-Yau surfaces
![]() $(Y^{1}, D^{1})$
and
$(Y^{1}, D^{1})$
and
![]() $(Y^{2}, D^{2})$
is an isomorphism
$(Y^{2}, D^{2})$
is an isomorphism
![]() $\theta : Y^{1} \rightarrow Y^{2}$
, with the property that
$\theta : Y^{1} \rightarrow Y^{2}$
, with the property that
![]() $\theta (D^{1}_{i}) = \theta (D^{2}_{i})$
for each boundary component
$\theta (D^{1}_{i}) = \theta (D^{2}_{i})$
for each boundary component
![]() $D^{k}_{i}$
of
$D^{k}_{i}$
of
![]() $D^{k}$
for
$D^{k}$
for
![]() $k = 1, 2$
, and
$k = 1, 2$
, and
![]() $\theta $
respects the orientations of
$\theta $
respects the orientations of
![]() $D^{1}$
and
$D^{1}$
and
![]() $D^{2}$
(automatic for
$D^{2}$
(automatic for
![]() $n \geq 3$
).
$n \geq 3$
).
Definition 3.17. Given any log Calabi-Yau surface
![]() $(Y, D)$
, the admissible group of Y is defined as follows:
$(Y, D)$
, the admissible group of Y is defined as follows:
 $$ \begin{align*} \operatorname{\text{Adm}} = \{ \theta \in \operatorname{\text{Aut}}(\operatorname{Pic}(Y)) \; \vert \; &\theta([D_{i}]) = [D_{i}] \text{ for all } i = 1, \dots, n \text{ and } \\ &\theta(\operatorname{Nef}(Y_{gen})) = \operatorname{Nef}(Y_{gen}) \}. \end{align*} $$
$$ \begin{align*} \operatorname{\text{Adm}} = \{ \theta \in \operatorname{\text{Aut}}(\operatorname{Pic}(Y)) \; \vert \; &\theta([D_{i}]) = [D_{i}] \text{ for all } i = 1, \dots, n \text{ and } \\ &\theta(\operatorname{Nef}(Y_{gen})) = \operatorname{Nef}(Y_{gen}) \}. \end{align*} $$
Remark 3.18.
![]() $\operatorname {\text {Adm}}$
is identified with the monodromy group for
$\operatorname {\text {Adm}}$
is identified with the monodromy group for
![]() $(Y, D)$
([Reference Gross, Hacking and KeelGHK15b], Theorem 5.15).
$(Y, D)$
([Reference Gross, Hacking and KeelGHK15b], Theorem 5.15).
Definition 3.19. Let
![]() $\Gamma $
be a group and X a topological space. Suppose that
$\Gamma $
be a group and X a topological space. Suppose that
![]() $\Gamma $
acts on X by homeomorphisms. We say that a closed subset
$\Gamma $
acts on X by homeomorphisms. We say that a closed subset
![]() $D \subset X$
is a fundamental domain for the action of
$D \subset X$
is a fundamental domain for the action of
![]() $\Gamma $
on X if the following are true:
$\Gamma $
on X if the following are true:
-
1. for all
 $x \in X$
, there exists
$x \in X$
, there exists
 $d \in D$
and
$d \in D$
and
 $\gamma \in \Gamma $
such that
$\gamma \in \Gamma $
such that
 $\gamma (d) = x$
; and
$\gamma (d) = x$
; and -
2. for all
 $\gamma _{1}, \gamma _{2} \in \Gamma $
such that
$\gamma _{1}, \gamma _{2} \in \Gamma $
such that
 $\gamma _{1} \neq \gamma _{2}$
, the intersection
$\gamma _{1} \neq \gamma _{2}$
, the intersection
 $\gamma _{1}D \cap \gamma _{2}D$
has empty interior.
$\gamma _{1}D \cap \gamma _{2}D$
has empty interior.
Definition 3.20. Given a log Calabi-Yau surface
![]() $(Y, D)$
, the period point is defined to be the homomorphism
$(Y, D)$
, the period point is defined to be the homomorphism
![]() $\phi : \langle D_{1}, \dots , D_{n} \rangle ^{\bot } \rightarrow \mathbb {C}^{\ast }$
, where a line bundle
$\phi : \langle D_{1}, \dots , D_{n} \rangle ^{\bot } \rightarrow \mathbb {C}^{\ast }$
, where a line bundle
![]() $L \in \langle D_{1}, \dots , D_{n} \rangle ^{\bot }$
is sent to
$L \in \langle D_{1}, \dots , D_{n} \rangle ^{\bot }$
is sent to
![]() $\theta ([L \vert _{D}]) \in \mathbb {C}^{\ast }$
, where
$\theta ([L \vert _{D}]) \in \mathbb {C}^{\ast }$
, where
![]() $\theta : \operatorname {Pic}^{0}(D) \xrightarrow {\sim } \mathbb {C}^{\ast }$
is the isomorphism determined by the given orientation of D (as explained in [Reference Gross, Hacking and KeelGHK15b], Lemma 2.1). Here,
$\theta : \operatorname {Pic}^{0}(D) \xrightarrow {\sim } \mathbb {C}^{\ast }$
is the isomorphism determined by the given orientation of D (as explained in [Reference Gross, Hacking and KeelGHK15b], Lemma 2.1). Here,
![]() $\operatorname {Pic}^{0}(D)$
is the kernel of the map
$\operatorname {Pic}^{0}(D)$
is the kernel of the map
![]() $c_{1}: \operatorname {Pic}(D) \rightarrow H^{2}(D, \mathbb {Z}) = \mathbb {Z}^{n}$
, given by
$c_{1}: \operatorname {Pic}(D) \rightarrow H^{2}(D, \mathbb {Z}) = \mathbb {Z}^{n}$
, given by
![]() $L \mapsto (\deg L \vert _{D_{i}})_{i=1}^{n}$
.
$L \mapsto (\deg L \vert _{D_{i}})_{i=1}^{n}$
.
By [Reference FriedmanF15], Proposition 3.12, the homomorphism
![]() $\phi $
is the extension class of the mixed Hodge structure on
$\phi $
is the extension class of the mixed Hodge structure on
![]() $H_{2}(U, \mathbb {C})$
, where we take
$H_{2}(U, \mathbb {C})$
, where we take
![]() $U = Y \setminus D$
. There is an exact sequence ([Reference LooijengaL81], Chapter I, Section 5.1):
$U = Y \setminus D$
. There is an exact sequence ([Reference LooijengaL81], Chapter I, Section 5.1):
There exists a unique log Calabi-Yau surface in each deformation type such that
![]() $\phi (\alpha ) = 1$
for all
$\phi (\alpha ) = 1$
for all
![]() $\alpha \in \langle D_{1}, \dots , D_{n} \rangle ^{\bot }$
(i.e., the mixed Hodge structure on
$\alpha \in \langle D_{1}, \dots , D_{n} \rangle ^{\bot }$
(i.e., the mixed Hodge structure on
![]() $H_{2}(U)$
is split). This follows from the Torelli theorem ([Reference Gross, Hacking and KeelGHK15b], §5; and [Reference FriedmanF15], Corollary 9.7). We denote this log Calabi-Yau surface by
$H_{2}(U)$
is split). This follows from the Torelli theorem ([Reference Gross, Hacking and KeelGHK15b], §5; and [Reference FriedmanF15], Corollary 9.7). We denote this log Calabi-Yau surface by
![]() $(Y_{e}, D_{e})$
.
$(Y_{e}, D_{e})$
.
Definition 3.21. Given a log Calabi-Yau surface
![]() $(Y, D)$
, the associated root system is the subset of
$(Y, D)$
, the associated root system is the subset of
![]() $\operatorname {Pic}(Y)$
defined by
$\operatorname {Pic}(Y)$
defined by
Definition 3.22. We define the Weyl group of the root system
![]() $\Phi \subset \operatorname {Pic}(Y)$
as follows:
$\Phi \subset \operatorname {Pic}(Y)$
as follows:
where the generators
![]() $s_{\alpha }(\beta ) = \beta + (\alpha \cdot \beta ) \alpha $
are the reflections in the hyperplanes
$s_{\alpha }(\beta ) = \beta + (\alpha \cdot \beta ) \alpha $
are the reflections in the hyperplanes
![]() $\alpha ^{\bot }$
for
$\alpha ^{\bot }$
for
![]() $\alpha \in \Phi $
.
$\alpha \in \Phi $
.
Definition 3.23. Given
![]() $(Y_{e}, D_{e})$
, we define the simple roots as the set
$(Y_{e}, D_{e})$
, we define the simple roots as the set
Proposition 3.24 ([Reference Gross, Hacking and KeelGHK15b], Proposition 3.4).
The set
![]() $\Delta $
is contained in
$\Delta $
is contained in
![]() $\Phi $
, and the Weyl group W is generated by the reflections
$\Phi $
, and the Weyl group W is generated by the reflections
![]() $s_{\delta }$
for
$s_{\delta }$
for
![]() $\delta \in \Delta $
– that is,
$\delta \in \Delta $
– that is,
By [Reference Gross, Hacking and KeelGHK15b], Lemma 2.15,
Remark 3.25. The Weyl group is a normal subgroup of
![]() $\operatorname {\text {Adm}}$
. (Proof: it follows from Definitions 3.17 and 3.21 that
$\operatorname {\text {Adm}}$
. (Proof: it follows from Definitions 3.17 and 3.21 that
![]() $\operatorname {\text {Adm}}$
preserves
$\operatorname {\text {Adm}}$
preserves
![]() $\Phi $
. If
$\Phi $
. If
![]() $g \in \operatorname {\text {Adm}}$
and
$g \in \operatorname {\text {Adm}}$
and
![]() $\alpha \in \Phi $
, then
$\alpha \in \Phi $
, then
![]() $g s_{\alpha } g^{-1} = s_{g(\alpha )}$
, which implies that
$g s_{\alpha } g^{-1} = s_{g(\alpha )}$
, which implies that
![]() $W \lhd \operatorname {\text {Adm}}$
).
$W \lhd \operatorname {\text {Adm}}$
).
By [Reference Gross, Hacking and KeelGHK15b], Theorem 3.2, the group W acts on
![]() $ {\operatorname {Nef}^{\; e}}(Y_{gen})$
with fundamental domain
$ {\operatorname {Nef}^{\; e}}(Y_{gen})$
with fundamental domain
![]() $ {\operatorname {Nef}^{\; e}}(Y_{e})$
. This is called the fundamental chamber in
$ {\operatorname {Nef}^{\; e}}(Y_{e})$
. This is called the fundamental chamber in
![]() $\operatorname {Nef}(Y_{gen})$
. By [Reference Gross, Hacking and KeelGHK15b], Theorem 5.1, there is an exact sequence
$\operatorname {Nef}(Y_{gen})$
. By [Reference Gross, Hacking and KeelGHK15b], Theorem 5.1, there is an exact sequence
where K is the kernel of the action of
![]() $\operatorname {\text {Aut}}(Y_{e}, D_{e})$
on
$\operatorname {\text {Aut}}(Y_{e}, D_{e})$
on
![]() $\operatorname {Pic}(Y)$
.
$\operatorname {Pic}(Y)$
.
4 Tools
Here, we include some main results that we use in the proof of our results.
Theorem 4.1 ([Reference Gross, Hacking and KeelGHK15b], Theorem 1.8, The global Torelli theorem for log Calabi-Yau surfaces).
Suppose that
![]() $(Y^{1}, D^{1})$
and
$(Y^{1}, D^{1})$
and
![]() $(Y^{2}, D^{2})$
are log Calabi-Yau surfaces. Consider the following three statements:
$(Y^{2}, D^{2})$
are log Calabi-Yau surfaces. Consider the following three statements:
-
1.
 $\theta : \operatorname {Pic}(Y^{1}) \rightarrow \operatorname {Pic}(Y^{2})$
is an isometry such that
$\theta : \operatorname {Pic}(Y^{1}) \rightarrow \operatorname {Pic}(Y^{2})$
is an isometry such that
 $\theta ([D_{i}^{1}]) = [D_{i}^{2}]$
for
$\theta ([D_{i}^{1}]) = [D_{i}^{2}]$
for
 $i = 1, \dots , n$
.
$i = 1, \dots , n$
. -
2.
 $\theta (L)$
is ample for some ample L on
$\theta (L)$
is ample for some ample L on
 $Y^{1}$
.
$Y^{1}$
. -
3.
 $\phi _{Y^{2}} \circ \theta = \phi _{Y^{1}}$
, where
$\phi _{Y^{2}} \circ \theta = \phi _{Y^{1}}$
, where
 $\phi _{Y}: \langle D_{1}, \dots , D_{n} \rangle ^{\bot } \rightarrow \mathbb {C}^{\ast }$
is the period point of Y.
$\phi _{Y}: \langle D_{1}, \dots , D_{n} \rangle ^{\bot } \rightarrow \mathbb {C}^{\ast }$
is the period point of Y.
![]() $(1), (2)$
and
$(1), (2)$
and
![]() $(3)$
hold if and only if
$(3)$
hold if and only if
![]() $\theta = f^{\ast }$
for some isomorphism
$\theta = f^{\ast }$
for some isomorphism
![]() $f: (Y^{2}, D^{2}) \rightarrow (Y^{1}, D^{1})$
.
$f: (Y^{2}, D^{2}) \rightarrow (Y^{1}, D^{1})$
.
Proposition 4.2 ([Reference Engel and FriedmanEF16], Proposition 1.5).
Let
![]() $(Y_{gen}, D_{gen})$
be a generic log Calabi-Yau surface, where
$(Y_{gen}, D_{gen})$
be a generic log Calabi-Yau surface, where
![]() $D_{gen}$
has at least three boundary components. If B is a divisor on
$D_{gen}$
has at least three boundary components. If B is a divisor on
![]() $Y_{gen}$
with nonnegative integer coefficients, then B is linearly equivalent to a divisor of the form
$Y_{gen}$
with nonnegative integer coefficients, then B is linearly equivalent to a divisor of the form
where the
![]() $E_{j}$
’s are disjoint interior
$E_{j}$
’s are disjoint interior
![]() $(-1)$
-curves and
$(-1)$
-curves and
![]() $a_{i}, b_{j}$
are nonnegative integers.
$a_{i}, b_{j}$
are nonnegative integers.
Remark 4.3. Although the Engel-Friedman Proposition 4.2 is stated for B with nonnegative integer coefficients, the statement also holds for B with nonnegative real coefficients. There is a sketch of the proof in the paper ([Reference Engel and FriedmanEF16], p.55), which uses a continuity argument and the assertion that the collection of subsets
 $$ \begin{align*} \bigg\{ {\sum a_{j}D_{j} + \sum b_{i}E_{i} \; \vert \; a_{j}, b_{i} \in \mathbb{R}_{\geq 0}} \bigg\}, \end{align*} $$
$$ \begin{align*} \bigg\{ {\sum a_{j}D_{j} + \sum b_{i}E_{i} \; \vert \; a_{j}, b_{i} \in \mathbb{R}_{\geq 0}} \bigg\}, \end{align*} $$
where the
![]() $E_{i}$
’s are disjoint interior
$E_{i}$
’s are disjoint interior
![]() $(-1)$
-curves, is locally finite in
$(-1)$
-curves, is locally finite in
![]() $ {\operatorname {Nef}^{\; e}}(Y_{gen})$
in a sense that is made precise below. Since this is important for our results, we give a complete proof (Proposition 4.10).
$ {\operatorname {Nef}^{\; e}}(Y_{gen})$
in a sense that is made precise below. Since this is important for our results, we give a complete proof (Proposition 4.10).
Friedman showed in [Reference FriedmanF15] that
![]() $\operatorname {\text {Adm}}$
acts with finitely many orbits on the set of faces of
$\operatorname {\text {Adm}}$
acts with finitely many orbits on the set of faces of
![]() $ {\operatorname {Nef}^{\; e}}(Y_{gen})$
corresponding to interior
$ {\operatorname {Nef}^{\; e}}(Y_{gen})$
corresponding to interior
![]() $(-1)$
-curves. This is stated in Theorem 4.4.
$(-1)$
-curves. This is stated in Theorem 4.4.
Theorem 4.4 (Friedman [Reference FriedmanF15], Theorem 9.8).
Let
![]() $(Y, D)$
be a generic log Calabi-Yau surface. Let
$(Y, D)$
be a generic log Calabi-Yau surface. Let
![]() $\mathcal {E}(Y, D)$
be the set of all interior
$\mathcal {E}(Y, D)$
be the set of all interior
![]() $(-1)$
-curves of Y. Then the admissible group
$(-1)$
-curves of Y. Then the admissible group
![]() $\operatorname {\text {Adm}}$
acts on
$\operatorname {\text {Adm}}$
acts on
![]() $\mathcal {E}(Y, D)$
, and there are finitely many
$\mathcal {E}(Y, D)$
, and there are finitely many
![]() $\operatorname {\text {Adm}}$
-orbits for this action.
$\operatorname {\text {Adm}}$
-orbits for this action.
The following Corollary 4.5 by Friedman is similar to the statement above. Specifically, it is a statement about the action of
![]() $\operatorname {\text {Adm}}$
on the set of collections of disjoint interior
$\operatorname {\text {Adm}}$
on the set of collections of disjoint interior
![]() $(-1)$
-curves.
$(-1)$
-curves.
Corollary 4.5 (Friedman [Reference FriedmanF15], Corollary 9.10).
Given a generic log Calabi-Yau surface
![]() $(Y, D)$
, let
$(Y, D)$
, let
![]() $\mathcal {E}_{k}(Y, D)$
be the set of collections
$\mathcal {E}_{k}(Y, D)$
be the set of collections
![]() $\{E_{1}, \dots , E_{k}\}$
, for any
$\{E_{1}, \dots , E_{k}\}$
, for any
![]() $k \in \mathbb {N}$
, where the curves
$k \in \mathbb {N}$
, where the curves
![]() $E_{i}$
are disjoint, interior
$E_{i}$
are disjoint, interior
![]() $(-1)$
-curves. Then the admissible group
$(-1)$
-curves. Then the admissible group
![]() $\operatorname {\text {Adm}}$
acts on
$\operatorname {\text {Adm}}$
acts on
![]() $\mathcal {E}_{k}(Y, D)$
, and the number of
$\mathcal {E}_{k}(Y, D)$
, and the number of
![]() $\operatorname {\text {Adm}}$
orbits for this action is finite.
$\operatorname {\text {Adm}}$
orbits for this action is finite.
Theorem 4.6 (Looijenga [Reference LooijengaL14], Proposition-Definition 4.1; and Application 4.14; and Proposition 4.7).
Let
![]() $\Gamma $
be a group and L be a lattice (i.e., a finitely generated free abelian group), and let
$\Gamma $
be a group and L be a lattice (i.e., a finitely generated free abelian group), and let
![]() $C \subset L \otimes _{\mathbb {Z}} \mathbb {R}$
be an open nondegenerate convex cone. Define
$C \subset L \otimes _{\mathbb {Z}} \mathbb {R}$
be an open nondegenerate convex cone. Define
Assume that
![]() $\Gamma $
acts on L faithfully, preserving the cone C. If there exists a polyhedral cone
$\Gamma $
acts on L faithfully, preserving the cone C. If there exists a polyhedral cone
![]() $\Pi \subset C_{+}$
such that
$\Pi \subset C_{+}$
such that
![]() $\Gamma \cdot \Pi = C_{+}$
, then there exists a rational polyhedral fundamental domain for the action of
$\Gamma \cdot \Pi = C_{+}$
, then there exists a rational polyhedral fundamental domain for the action of
![]() $\Gamma $
on
$\Gamma $
on
![]() $C_{+}$
. Moreover, in this case, the group
$C_{+}$
. Moreover, in this case, the group
![]() $N_{\Gamma } F / Z_{\Gamma } F$
acts on any face F of
$N_{\Gamma } F / Z_{\Gamma } F$
acts on any face F of
![]() $C_{+}$
with a rational polyhedral fundamental domain.
$C_{+}$
with a rational polyhedral fundamental domain.
Remark 4.7. In Theorem 4.6, following the notation of Looijenga, we use
![]() $N_{\Gamma } F$
to mean the normalizer of F in
$N_{\Gamma } F$
to mean the normalizer of F in
![]() $\Gamma $
and
$\Gamma $
and
![]() $Z_{\Gamma } F$
to mean the centralizer (i.e., elements of
$Z_{\Gamma } F$
to mean the centralizer (i.e., elements of
![]() $\Gamma $
that fix F pointwise). The last statement is a special case of Proposition 4.7 in [Reference LooijengaL14].
$\Gamma $
that fix F pointwise). The last statement is a special case of Proposition 4.7 in [Reference LooijengaL14].
Proposition 4.8. Let
![]() $(Y_{gen}, D_{gen})$
be a generic log Calabi-Yau surface. For a collection
$(Y_{gen}, D_{gen})$
be a generic log Calabi-Yau surface. For a collection
![]() $\{E_{1}, \dots , E_{k}\}$
of disjoint
$\{E_{1}, \dots , E_{k}\}$
of disjoint
![]() $(-1)$
-curves, define
$(-1)$
-curves, define
Then
-
1.
 $C^{\prime }(E_{1}, \dots , E_{k})$
is a rational polyhedral cone; and
$C^{\prime }(E_{1}, \dots , E_{k})$
is a rational polyhedral cone; and -
2. If
 $D_{gen}$
consists of at least three components, then the set of cones
$D_{gen}$
consists of at least three components, then the set of cones
 $C^{\prime }(E_{1}, \dots , E_{k})$
covers
$C^{\prime }(E_{1}, \dots , E_{k})$
covers
 $ {\operatorname {Nef}^{\; e}}(Y^{\prime }_{gen})$
.
$ {\operatorname {Nef}^{\; e}}(Y^{\prime }_{gen})$
.
Proof. Let C be the cone defined by
so that
![]() $C^{\prime }(E_{1}, \dots , E_{k})$
can be expressed as
$C^{\prime }(E_{1}, \dots , E_{k})$
can be expressed as
![]() $C \cap {\operatorname {Nef}^{\; e}}(Y_{gen})$
. The cone
$C \cap {\operatorname {Nef}^{\; e}}(Y_{gen})$
. The cone
![]() $C^{\prime }(E_{1}, \dots , E_{k})$
is rational polyhedral because C is rational polyhedral by definition, and the intersection with the nef cone is given by finitely many inequalities
$C^{\prime }(E_{1}, \dots , E_{k})$
is rational polyhedral because C is rational polyhedral by definition, and the intersection with the nef cone is given by finitely many inequalities
![]() $L \cdot D_{i} \geq 0$
and
$L \cdot D_{i} \geq 0$
and
![]() $L \cdot E_{j} \geq 0$
for all
$L \cdot E_{j} \geq 0$
for all
![]() $1 \leq i \leq n$
and all
$1 \leq i \leq n$
and all
![]() $1 \leq j \leq k$
. This shows that
$1 \leq j \leq k$
. This shows that
![]() $C^{\prime }(E_{1}, \dots , E_{k})$
is rational polyhedral. Now assume that
$C^{\prime }(E_{1}, \dots , E_{k})$
is rational polyhedral. Now assume that
![]() $D_{gen}$
has at least three components. Then, by Proposition 4.10,
$D_{gen}$
has at least three components. Then, by Proposition 4.10,
where the union is over the set
![]() $\displaystyle {\bigcup _{k} \mathcal {E}_{k}(Y, D)}$
of collections
$\displaystyle {\bigcup _{k} \mathcal {E}_{k}(Y, D)}$
of collections
![]() $\{E_{1}, \dots , E_{k}\}$
of disjoint interior
$\{E_{1}, \dots , E_{k}\}$
of disjoint interior
![]() $(-1)$
-curves.
$(-1)$
-curves.
Theorem 4.9 (The Siegel Property, as stated in [Reference LooijengaL14], Theorem 3.8).
Let L be a lattice and
![]() $V = L \otimes \mathbb {R}$
. Let
$V = L \otimes \mathbb {R}$
. Let
![]() $C \subset V$
be an open convex nondegenerate cone. We denote the convex hull
$C \subset V$
be an open convex nondegenerate cone. We denote the convex hull
![]() $\operatorname {\text {Conv}}(\bar {C} \cap L)$
by
$\operatorname {\text {Conv}}(\bar {C} \cap L)$
by
![]() $C_{+}$
. Let
$C_{+}$
. Let
![]() $\Gamma $
be a subgroup of
$\Gamma $
be a subgroup of
![]() $GL(V)$
such that
$GL(V)$
such that
![]() $\Gamma $
leaves the cone C and the lattice L invariant. Then
$\Gamma $
leaves the cone C and the lattice L invariant. Then
![]() $\Gamma $
has the Siegel Property in
$\Gamma $
has the Siegel Property in
![]() $C_{+}$
; that is, if
$C_{+}$
; that is, if
![]() $\Pi _{1}$
and
$\Pi _{1}$
and
![]() $\Pi _{2}$
are polyhedral cones in
$\Pi _{2}$
are polyhedral cones in
![]() $C_{+}$
, then the collection
$C_{+}$
, then the collection
![]() $\{\gamma \Pi _{1} \bigcap \Pi _{2}\}_{\gamma \in \Gamma }$
is finite.
$\{\gamma \Pi _{1} \bigcap \Pi _{2}\}_{\gamma \in \Gamma }$
is finite.
Next, we give the precise statement of Engel-Friedman’s Proposition 4.2 for real coefficients, followed by a careful proof, which uses the Siegel Property 4.9 and the result 4.5 of Friedman.
Proposition 4.10 (Proposition 4.2 for B with real coefficients).
Let
![]() $(Y_{gen}, D_{gen})$
be a generic log Calabi-Yau surface, where
$(Y_{gen}, D_{gen})$
be a generic log Calabi-Yau surface, where
![]() $D_{gen}$
has at least three boundary components. If B is a divisor on
$D_{gen}$
has at least three boundary components. If B is a divisor on
![]() $Y_{gen}$
with nonnegative real coefficients, then B is
$Y_{gen}$
with nonnegative real coefficients, then B is
![]() $\mathbb {R}$
-linearly equivalent to a divisor of the form
$\mathbb {R}$
-linearly equivalent to a divisor of the form
where the
![]() $E_{j}$
’s are disjoint interior
$E_{j}$
’s are disjoint interior
![]() $(-1)$
-curves and
$(-1)$
-curves and
![]() $a_{i}, b_{j}$
are nonnegative real numbers.
$a_{i}, b_{j}$
are nonnegative real numbers.
Proof. We use the same notation introduced in Proposition 4.8 above; that is, for a log Calabi-Yau surface
![]() $(Y_{gen}, D_{gen})$
where
$(Y_{gen}, D_{gen})$
where
![]() $D_{gen}$
is of length at least three, we let
$D_{gen}$
is of length at least three, we let
We want to show that
where
![]() $\operatorname {\text {Curv}}(Y) := \{ \sum a_{i} [C_{j}] \; \vert \; a_{i} \in \mathbb {R}_{\geq 0} \text { and } C_{i} \subset Y \text { are irreducible curves}\}$
(Note, because
$\operatorname {\text {Curv}}(Y) := \{ \sum a_{i} [C_{j}] \; \vert \; a_{i} \in \mathbb {R}_{\geq 0} \text { and } C_{i} \subset Y \text { are irreducible curves}\}$
(Note, because
![]() $\dim (Y_{gen}) = 2$
, the cones
$\dim (Y_{gen}) = 2$
, the cones
![]() $\operatorname {Eff}(Y_{gen})$
and
$\operatorname {Eff}(Y_{gen})$
and
![]() $\operatorname {\text {Curv}}(Y_{gen})$
coincide). Clearly,
$\operatorname {\text {Curv}}(Y_{gen})$
coincide). Clearly,
where the union is taken over all
![]() $C(E_{1}, \dots , E_{k})$
where
$C(E_{1}, \dots , E_{k})$
where
![]() $\{E_{1}, \dots , E_{k}\}$
are collections of disjoint interior
$\{E_{1}, \dots , E_{k}\}$
are collections of disjoint interior
![]() $(-1)$
-curves.
$(-1)$
-curves.
Let
![]() $x \in \operatorname {\text {Curv}}(Y_{gen})$
be an arbitrary point. A convex cone is the disjoint union of the relative interiors of its faces. This follows from the supporting hyperplane theorem ([Reference SimonS11], Proposition 8.5).
$x \in \operatorname {\text {Curv}}(Y_{gen})$
be an arbitrary point. A convex cone is the disjoint union of the relative interiors of its faces. This follows from the supporting hyperplane theorem ([Reference SimonS11], Proposition 8.5).
So
![]() $x \in \operatorname {relInt}(F)$
, where F is some face of
$x \in \operatorname {relInt}(F)$
, where F is some face of
![]() $\operatorname {\text {Curv}}(Y_{gen})$
(possibly
$\operatorname {\text {Curv}}(Y_{gen})$
(possibly
![]() $F = \operatorname {\text {Curv}}(Y_{gen})$
). Since
$F = \operatorname {\text {Curv}}(Y_{gen})$
). Since
![]() $\operatorname {\text {Curv}}(Y_{gen})$
is generated by rational points, the same is true for any face of
$\operatorname {\text {Curv}}(Y_{gen})$
is generated by rational points, the same is true for any face of
![]() $\operatorname {\text {Curv}}(Y_{gen})$
. In particular, the face F is the convex hull of its rational points, so the rational points are dense in F. Thus, we may choose a sequence of points
$\operatorname {\text {Curv}}(Y_{gen})$
. In particular, the face F is the convex hull of its rational points, so the rational points are dense in F. Thus, we may choose a sequence of points
![]() $x_{n} \in F \; \bigcap \; (\operatorname {Pic}(Y) \otimes \mathbb {Q})$
that converge to x as n approaches infinity. The original Engel-Friedman statement (see Proposition 4.2) was stated for integer coefficients, but this implies that the statement for rational coefficeints is also true. So for every n, the point
$x_{n} \in F \; \bigcap \; (\operatorname {Pic}(Y) \otimes \mathbb {Q})$
that converge to x as n approaches infinity. The original Engel-Friedman statement (see Proposition 4.2) was stated for integer coefficients, but this implies that the statement for rational coefficeints is also true. So for every n, the point
![]() $x_{n}$
belongs to some cone
$x_{n}$
belongs to some cone
![]() $C(E_{1}, \dots , E_{k})$
, as defined above.
$C(E_{1}, \dots , E_{k})$
, as defined above.
Since
![]() $x \in \operatorname {relInt}(F)$
(i.e., the interior of F regarded as a subset of
$x \in \operatorname {relInt}(F)$
(i.e., the interior of F regarded as a subset of
![]() $\langle F \rangle _{\mathbb {R}}$
), there exists a rational polyhedral cone
$\langle F \rangle _{\mathbb {R}}$
), there exists a rational polyhedral cone
![]() $\Pi \subset F$
such that
$\Pi \subset F$
such that
![]() $x \in \operatorname {relInt}(\Pi )$
and
$x \in \operatorname {relInt}(\Pi )$
and
![]() $\dim (\Pi ) = \dim (F)$
. Then
$\dim (\Pi ) = \dim (F)$
. Then
![]() $\operatorname {relInt}(\Pi )$
is an open subset of F. Since the points
$\operatorname {relInt}(\Pi )$
is an open subset of F. Since the points
![]() $\{x_{n}\}$
converge to x in the face F, there exists some number
$\{x_{n}\}$
converge to x in the face F, there exists some number
![]() $N \in \mathbb {N}$
such that
$N \in \mathbb {N}$
such that
![]() $x_{n} \in \Pi $
for all
$x_{n} \in \Pi $
for all
![]() $n \geq N$
. Friedman’s results tells us that
$n \geq N$
. Friedman’s results tells us that
![]() $\operatorname {\text {Adm}}$
acts on the cones
$\operatorname {\text {Adm}}$
acts on the cones
![]() $C(E_{1}, \dots , E_{k})$
with finitely many orbits. Say we choose a representative
$C(E_{1}, \dots , E_{k})$
with finitely many orbits. Say we choose a representative
![]() $C_{i}$
from each orbit, so we have finitely many representatives
$C_{i}$
from each orbit, so we have finitely many representatives
![]() $C_{1}, \dots , C_{r}$
(note that we drop the
$C_{1}, \dots , C_{r}$
(note that we drop the
![]() $\{E_{1}, \dots , E_{k}\}$
part here to keep the notation simpler). By the Siegel property 4.9, there exists finitely many elements
$\{E_{1}, \dots , E_{k}\}$
part here to keep the notation simpler). By the Siegel property 4.9, there exists finitely many elements
![]() $g \in \operatorname {\text {Adm}}$
such that
$g \in \operatorname {\text {Adm}}$
such that
![]() $g(C_{i}) \; \bigcap \Pi \neq \emptyset $
. Suppose these elements are
$g(C_{i}) \; \bigcap \Pi \neq \emptyset $
. Suppose these elements are
![]() $g_{i, 1}, \dots , g_{i, m_{i}}$
for
$g_{i, 1}, \dots , g_{i, m_{i}}$
for
![]() $i = 1, \dots , r$
. Then the following cones intersect
$i = 1, \dots , r$
. Then the following cones intersect
![]() $\Pi $
:
$\Pi $
:
 $$ \begin{align*} &g_{1, 1} C_{1}, \dots, g_{1, m_{1}} C_{1} \\ &g_{2, 1} C_{2}, \dots, g_{2, m_{2}} C_{2} \\ &\vdots \\ &g_{r, 1} C_{r}, \dots, g_{r, m_{r}} C_{r}. \end{align*} $$
$$ \begin{align*} &g_{1, 1} C_{1}, \dots, g_{1, m_{1}} C_{1} \\ &g_{2, 1} C_{2}, \dots, g_{2, m_{2}} C_{2} \\ &\vdots \\ &g_{r, 1} C_{r}, \dots, g_{r, m_{r}} C_{r}. \end{align*} $$
As a result, we have a (finite) total of
![]() $m = m_{1} + \dots + m_{r}$
cones
$m = m_{1} + \dots + m_{r}$
cones
![]() $\sigma _{l}$
of the form
$\sigma _{l}$
of the form
![]() $C(E_{1}, \dots , E_{k})$
intersecting the cone
$C(E_{1}, \dots , E_{k})$
intersecting the cone
![]() $\Pi $
. Since each cone
$\Pi $
. Since each cone
![]() $C(E_{1}, \dots , E_{k})$
is closed, the finite union
$C(E_{1}, \dots , E_{k})$
is closed, the finite union
is also closed. Recall that each
![]() $x_{n}$
is contained in some cone in the union above, so their limit point x must also lie in the union; that is,
$x_{n}$
is contained in some cone in the union above, so their limit point x must also lie in the union; that is,
 $$ \begin{align*} x \in {\bigcup_{l=1}^{m} \sigma_{l}} \subset \displaystyle{\bigcup \; C(E_{1}, \dots, E_{k})}. \end{align*} $$
$$ \begin{align*} x \in {\bigcup_{l=1}^{m} \sigma_{l}} \subset \displaystyle{\bigcup \; C(E_{1}, \dots, E_{k})}. \end{align*} $$
Now we have shown that
![]() $\operatorname {\text {Curv}}(Y_{gen}) \subseteq \bigcup C(E_{1}, \dots , E_{k})$
. Therefore,
$\operatorname {\text {Curv}}(Y_{gen}) \subseteq \bigcup C(E_{1}, \dots , E_{k})$
. Therefore,
proving Proposition 4.10.
Theorem 4.12. Let
![]() $(Y_{e}, D_{e})$
be a log Calabi-Yau surface with split mixed Hodge structure. If L is a nef divisor on Y, then L is semiample.
$(Y_{e}, D_{e})$
be a log Calabi-Yau surface with split mixed Hodge structure. If L is a nef divisor on Y, then L is semiample.
Proof. Let L be nef on Y. Then
![]() $L^{2} \geq 0$
. If
$L^{2} \geq 0$
. If
![]() $L^{2}> 0$
, then by Theorem 4.8 of [Reference FriedmanF15], the divisor L is semiample. For the remainder of this proof, we suppose that
$L^{2}> 0$
, then by Theorem 4.8 of [Reference FriedmanF15], the divisor L is semiample. For the remainder of this proof, we suppose that
![]() $L^{2} = 0$
and
$L^{2} = 0$
and
![]() $L \neq 0$
. Using Riemann-Roch, we obtain
$L \neq 0$
. Using Riemann-Roch, we obtain
 $$ \begin{align*} \chi(L) &= \chi(\mathcal{O}) + \displaystyle{\frac{1}{2}} L \cdot (L - K_{Y}) \\ &= 1 + \displaystyle{\frac{1}{2}} L^{2} + \displaystyle{\frac{1}{2}} (L \cdot D) \; \; \; \text{since }Y\text{ is rational and }K_{Y} + D = 0 \\ &= 1 + \displaystyle{\frac{1}{2}} (L \cdot D) \; \; \; \text{using }L^{2} = 0. \end{align*} $$
$$ \begin{align*} \chi(L) &= \chi(\mathcal{O}) + \displaystyle{\frac{1}{2}} L \cdot (L - K_{Y}) \\ &= 1 + \displaystyle{\frac{1}{2}} L^{2} + \displaystyle{\frac{1}{2}} (L \cdot D) \; \; \; \text{since }Y\text{ is rational and }K_{Y} + D = 0 \\ &= 1 + \displaystyle{\frac{1}{2}} (L \cdot D) \; \; \; \text{using }L^{2} = 0. \end{align*} $$
Here, we note that
![]() $\chi (L) \geq 1$
, since L nef and D effective imply that
$\chi (L) \geq 1$
, since L nef and D effective imply that
![]() $L \cdot D \geq 0$
. However, the Euler characteristic of L may also be expressed as
$L \cdot D \geq 0$
. However, the Euler characteristic of L may also be expressed as
By the last paragraph of the proof of Lemma 3.12, since L is nef, we have
![]() $h^{2}(L) = 0$
. Now
$h^{2}(L) = 0$
. Now
![]() $\chi (L) = h^{0}(L) - h^{1}(L) = 1 + \displaystyle {\frac {1}{2}} (L \cdot D)$
. Next we split the inequality
$\chi (L) = h^{0}(L) - h^{1}(L) = 1 + \displaystyle {\frac {1}{2}} (L \cdot D)$
. Next we split the inequality
![]() $L \cdot D \geq 0$
(which comes from L being nef) into two subcases, and in each situation, we prove that
$L \cdot D \geq 0$
(which comes from L being nef) into two subcases, and in each situation, we prove that
![]() $h^{0}(L) \geq 2$
.
$h^{0}(L) \geq 2$
.
Subcase (i). Suppose that
![]() $L \cdot D> 0$
, or
$L \cdot D> 0$
, or
![]() $L \cdot D \geq 1$
. Then,
$L \cdot D \geq 1$
. Then,
Since
![]() $\chi (L) \in \mathbb {Z}$
, we have
$\chi (L) \in \mathbb {Z}$
, we have
![]() $h^{0}(L) \geq 2$
.
$h^{0}(L) \geq 2$
.
Subcase (ii). Suppose that
![]() $L \cdot D = 0$
. We have
$L \cdot D = 0$
. We have
![]() $\chi (L) = h^{0}(L) - h^{1}(L) = 1$
. We show that
$\chi (L) = h^{0}(L) - h^{1}(L) = 1$
. We show that
![]() $h^{1}(L) \geq 1$
, so
$h^{1}(L) \geq 1$
, so
![]() $h^{0}(L) \geq 2$
. Since
$h^{0}(L) \geq 2$
. Since
![]() $L \cdot D = 0$
and L is nef, we have
$L \cdot D = 0$
and L is nef, we have
![]() $L \cdot D_{i} = 0$
for all i. Then because
$L \cdot D_{i} = 0$
for all i. Then because
![]() $(Y, D)$
has split mixed Hodge structure, it follows that
$(Y, D)$
has split mixed Hodge structure, it follows that
![]() $\mathcal {O}_{D}(L \vert _{D}) \simeq \mathcal {O}_{D}$
(Section 3). From the exact sequence
$\mathcal {O}_{D}(L \vert _{D}) \simeq \mathcal {O}_{D}$
(Section 3). From the exact sequence
we obtain

By Serre Duality, we have
 $$ \begin{align*} h^{2}(\mathcal{O}_{Y}(L-D)) &= h^{0}(\mathcal{O}_{Y}(K_{Y} - (L-D))) \\ &= h^{0}(\mathcal{O}_{Y}(-L)) \; \; \; \text{since }K_{Y} + D = 0 \\ &= 0. \end{align*} $$
$$ \begin{align*} h^{2}(\mathcal{O}_{Y}(L-D)) &= h^{0}(\mathcal{O}_{Y}(K_{Y} - (L-D))) \\ &= h^{0}(\mathcal{O}_{Y}(-L)) \; \; \; \text{since }K_{Y} + D = 0 \\ &= 0. \end{align*} $$
Then the map
![]() $\delta $
in the exact sequence above is surjective, so
$\delta $
in the exact sequence above is surjective, so
![]() $h^{1}(L) \geq 1$
.
$h^{1}(L) \geq 1$
.
Therefore,
![]() $h^{0}(L) \geq 2$
. This means that in the linear system
$h^{0}(L) \geq 2$
. This means that in the linear system
![]() $\vert L \vert $
, there is a moving part. Writing
$\vert L \vert $
, there is a moving part. Writing
![]() $L = M + F$
, where M is the moving part and F is the fixed part, we have
$L = M + F$
, where M is the moving part and F is the fixed part, we have
 $$ \begin{align*} L^{2} &= L \cdot (M + F) \\ &= L \cdot M + L \cdot F, \end{align*} $$
$$ \begin{align*} L^{2} &= L \cdot (M + F) \\ &= L \cdot M + L \cdot F, \end{align*} $$
and L nef gives
![]() $L \cdot M \geq 0$
and
$L \cdot M \geq 0$
and
![]() $L \cdot F \geq 0$
. Since
$L \cdot F \geq 0$
. Since
![]() $L^{2} = 0$
by assumption, we obtain
$L^{2} = 0$
by assumption, we obtain
![]() $L \cdot M = 0 = L \cdot F$
. Now we have
$L \cdot M = 0 = L \cdot F$
. Now we have
 $$ \begin{align*} L \cdot M &= (M + F) \cdot M \\ &= M^{2} + M \cdot F \\ &= 0, \end{align*} $$
$$ \begin{align*} L \cdot M &= (M + F) \cdot M \\ &= M^{2} + M \cdot F \\ &= 0, \end{align*} $$
and M is nef (since it is moving) so
![]() $M^{2} \geq 0$
and
$M^{2} \geq 0$
and
![]() $M \cdot F \geq 0$
, so
$M \cdot F \geq 0$
, so
![]() $M^{2} = M \cdot F = 0$
. Now
$M^{2} = M \cdot F = 0$
. Now
![]() $L \cdot F = \vert M + F \vert \cdot F = 0$
, and thus,
$L \cdot F = \vert M + F \vert \cdot F = 0$
, and thus,
![]() $F^{2} = 0$
. We make two conclusions from the computations above.
$F^{2} = 0$
. We make two conclusions from the computations above.
-
(a) The linear system
 $\vert M \vert $
has no fixed part, so
$\vert M \vert $
has no fixed part, so
 $\vert M \vert $
is basepoint free: there exists
$\vert M \vert $
is basepoint free: there exists
 $M^{\prime } \sim M$
such that M and
$M^{\prime } \sim M$
such that M and
 $M^{\prime }$
have no common components (since M is moving). Then
$M^{\prime }$
have no common components (since M is moving). Then
 $M \cdot M^{\prime } = M^{2} = 0$
, so
$M \cdot M^{\prime } = M^{2} = 0$
, so
 $\operatorname {\text {Supp}}(M) \cap \operatorname {\text {Supp}}(M^{\prime }) = \emptyset $
, and therefore,
$\operatorname {\text {Supp}}(M) \cap \operatorname {\text {Supp}}(M^{\prime }) = \emptyset $
, and therefore,
 $\vert M \vert $
is basepoint free. It follows that there exists a map
$\vert M \vert $
is basepoint free. It follows that there exists a map
 $\phi _{\vert M \vert }: Y \rightarrow C$
, where
$\phi _{\vert M \vert }: Y \rightarrow C$
, where
 $C \subset \mathbb {P}^{N}$
is a curve. By Stein factorization (see Hartshorne [Reference HartshorneH77], Chapter III (11.5)), replacing
$C \subset \mathbb {P}^{N}$
is a curve. By Stein factorization (see Hartshorne [Reference HartshorneH77], Chapter III (11.5)), replacing
 $L = M + F$
by
$L = M + F$
by
 $kL = kM + kF$
for sufficiently large k, we may assume that C is a smooth curve and
$kL = kM + kF$
for sufficiently large k, we may assume that C is a smooth curve and
 $\phi $
has connected fibers.
$\phi $
has connected fibers. -
(b) Secondly, we conclude that L is semiample, using the results that
 $F^{2} = 0$
and
$F^{2} = 0$
and
 $F \cdot M = 0$
. Since
$F \cdot M = 0$
. Since
 $F \cdot M = 0$
, the divisor F is contained in a union of fibers of the map
$F \cdot M = 0$
, the divisor F is contained in a union of fibers of the map
 $\phi : Y \rightarrow C$
. A fiber has negative semidefinite intersection matrix with kernel generated over
$\phi : Y \rightarrow C$
. A fiber has negative semidefinite intersection matrix with kernel generated over
 $\mathbb {Q}$
by the class of the fiber. Therefore,
$\mathbb {Q}$
by the class of the fiber. Therefore,
 $kF$
is a sum of fibers for some
$kF$
is a sum of fibers for some
 $k> 0$
. Then
$k> 0$
. Then
 $k^{\prime }F$
is basepoint free for some
$k^{\prime }F$
is basepoint free for some
 $k^{\prime }> 0$
such that
$k^{\prime }> 0$
such that
 $k \vert k^{\prime }$
by Riemann-Roch on the curve C. Now
$k \vert k^{\prime }$
by Riemann-Roch on the curve C. Now
 $k^{\prime } \cdot L = k^{\prime } \cdot M + k^{\prime } \cdot F$
is basepoint free, so L is semiample.
$k^{\prime } \cdot L = k^{\prime } \cdot M + k^{\prime } \cdot F$
is basepoint free, so L is semiample.
5 Proof of the conjecture
Theorem 5.1. The cone conjecture for
![]() $Y_{gen}$
holds. That is, the group
$Y_{gen}$
holds. That is, the group
![]() $\operatorname {\text {Adm}}$
acts on
$\operatorname {\text {Adm}}$
acts on
![]() $ {\operatorname {Nef}^{\; e}}(Y_{gen})$
with a rational polyhedral fundamental domain.
$ {\operatorname {Nef}^{\; e}}(Y_{gen})$
with a rational polyhedral fundamental domain.
Proof. First, assume
![]() $n \geq 3$
. By Friedman’s result (Corollary 4.5), the group
$n \geq 3$
. By Friedman’s result (Corollary 4.5), the group
![]() $\operatorname {\text {Adm}}$
acts on the set of finite collections of disjoint interior
$\operatorname {\text {Adm}}$
acts on the set of finite collections of disjoint interior
![]() $(-1)$
-curves with finitely many orbits. Let
$(-1)$
-curves with finitely many orbits. Let
![]() $C_{1}^{\prime }, \dots , C_{r}^{\prime }$
be representatives for the finitely many orbits of
$C_{1}^{\prime }, \dots , C_{r}^{\prime }$
be representatives for the finitely many orbits of
![]() $\operatorname {\text {Adm}}$
on the set of cones
$\operatorname {\text {Adm}}$
on the set of cones
![]() $C^{\prime }$
of Proposition 4.8. Let
$C^{\prime }$
of Proposition 4.8. Let
![]() $\Pi = \operatorname {\text {Conv}}(C_{1}^{\prime }, \dots , C_{r}^{\prime })$
. Then
$\Pi = \operatorname {\text {Conv}}(C_{1}^{\prime }, \dots , C_{r}^{\prime })$
. Then
![]() $\Pi $
is rational polyhedral because the cones
$\Pi $
is rational polyhedral because the cones
![]() $C^{\prime }_{i}$
are, by Proposition 4.8 (1). Moreover,
$C^{\prime }_{i}$
are, by Proposition 4.8 (1). Moreover,
![]() $\operatorname {\text {Adm}} \cdot \Pi = {\operatorname {Nef}^{\; e}}(Y_{gen})$
by Proposition 4.8 (2). Therefore,
$\operatorname {\text {Adm}} \cdot \Pi = {\operatorname {Nef}^{\; e}}(Y_{gen})$
by Proposition 4.8 (2). Therefore,
![]() $\operatorname {\text {Adm}}$
acts on
$\operatorname {\text {Adm}}$
acts on
![]() $ {\operatorname {Nef}^{\; e}}(Y_{gen})$
with a rational polyhedral fundamental domain by Theorem 4.6 of Looijenga: in our setting, the lattice L is
$ {\operatorname {Nef}^{\; e}}(Y_{gen})$
with a rational polyhedral fundamental domain by Theorem 4.6 of Looijenga: in our setting, the lattice L is
![]() $\operatorname {Pic}(Y_{gen})$
and C is the ample cone of
$\operatorname {Pic}(Y_{gen})$
and C is the ample cone of
![]() $Y_{gen}$
(which is the interior of
$Y_{gen}$
(which is the interior of
![]() $\operatorname {Nef}(Y_{gen})$
). Its closure
$\operatorname {Nef}(Y_{gen})$
). Its closure
![]() $\bar {C}$
is
$\bar {C}$
is
![]() $\operatorname {Nef}(Y_{gen})$
. The group
$\operatorname {Nef}(Y_{gen})$
. The group
![]() $\Gamma $
acting on L is
$\Gamma $
acting on L is
![]() $\operatorname {\text {Adm}}$
. By (3.3),
$\operatorname {\text {Adm}}$
. By (3.3),
![]() $C_{+} = {\operatorname {Nef}^{\; e}}(Y_{gen})$
. This proves the cone conjecture for
$C_{+} = {\operatorname {Nef}^{\; e}}(Y_{gen})$
. This proves the cone conjecture for
![]() $Y_{gen}$
in the case when
$Y_{gen}$
in the case when
![]() $D_{gen}$
has at least three components.
$D_{gen}$
has at least three components.
If the number of components n of
![]() $D_{gen}$
is one or two, then we show below in Section 6 that the nef cone is rational polyhedral for
$D_{gen}$
is one or two, then we show below in Section 6 that the nef cone is rational polyhedral for
![]() $Y_{e}$
. Moreover, in these cases, the groups
$Y_{e}$
. Moreover, in these cases, the groups
![]() $\operatorname {\text {Adm}}$
and the Weyl group W are equal ([Reference LooijengaL81], Proposition 4.7 or [Reference FriedmanF15], Theorem 9.13). Because the action of W on
$\operatorname {\text {Adm}}$
and the Weyl group W are equal ([Reference LooijengaL81], Proposition 4.7 or [Reference FriedmanF15], Theorem 9.13). Because the action of W on
![]() $ {\operatorname {Nef}^{\; e}}(Y_{gen})$
has fundamental domain
$ {\operatorname {Nef}^{\; e}}(Y_{gen})$
has fundamental domain
![]() $ {\operatorname {Nef}^{\; e}}(Y_{e})$
([Reference Gross, Hacking and KeelGHK15b], Theorem 3.2), we conclude that
$ {\operatorname {Nef}^{\; e}}(Y_{e})$
([Reference Gross, Hacking and KeelGHK15b], Theorem 3.2), we conclude that
![]() $\operatorname {\text {Adm}} = W$
acts on
$\operatorname {\text {Adm}} = W$
acts on
![]() $ {\operatorname {Nef}^{\; e}}(Y_{gen})$
with the rational polyhedral fundamental domain
$ {\operatorname {Nef}^{\; e}}(Y_{gen})$
with the rational polyhedral fundamental domain
![]() $\operatorname {Nef}(Y_{e})$
, proving the cone conjecture.
$\operatorname {Nef}(Y_{e})$
, proving the cone conjecture.
Theorem 5.2. The cone conjecture for
![]() $Y^{\prime }_{gen}$
holds. That is, the group
$Y^{\prime }_{gen}$
holds. That is, the group
![]() $\operatorname {\text {Adm}}$
acts on
$\operatorname {\text {Adm}}$
acts on
![]() $ {\operatorname {Nef}^{\; e}}(Y^{\prime }_{gen})$
with a rational polyhedral fundamental domain.
$ {\operatorname {Nef}^{\; e}}(Y^{\prime }_{gen})$
with a rational polyhedral fundamental domain.
Remark 5.3. We use the definition of
![]() $ {\operatorname {Nef}^{\; e}}(Y^{\prime }_{gen})$
as given in 3.15.
$ {\operatorname {Nef}^{\; e}}(Y^{\prime }_{gen})$
as given in 3.15.
Proof. By Theorem 5.1, we know that the cone conjecture holds for
![]() $Y_{gen}$
. Since
$Y_{gen}$
. Since
![]() $ {\operatorname {Nef}^{\; e}}(Y^{\prime }_{gen})$
is a face F of
$ {\operatorname {Nef}^{\; e}}(Y^{\prime }_{gen})$
is a face F of
![]() $ {\operatorname {Nef}^{\; e}}(Y_{gen})$
, by Looijenga’s result (see the last statement of Theorem 4.6), the cone conjecture also holds for
$ {\operatorname {Nef}^{\; e}}(Y_{gen})$
, by Looijenga’s result (see the last statement of Theorem 4.6), the cone conjecture also holds for
![]() $Y^{\prime }_{gen}$
. In our setting, the normalizer
$Y^{\prime }_{gen}$
. In our setting, the normalizer
![]() $N_{\Gamma }F$
is
$N_{\Gamma }F$
is
![]() $\operatorname {\text {Adm}}$
and the centralizer
$\operatorname {\text {Adm}}$
and the centralizer
![]() $Z_{\Gamma }F$
is
$Z_{\Gamma }F$
is
![]() $\{e\}$
.
$\{e\}$
.
Theorem 5.4. Let K be the kernel of the action of
![]() $\operatorname {\text {Aut}}(Y_{e}. D_{e})$
on
$\operatorname {\text {Aut}}(Y_{e}. D_{e})$
on
![]() $\operatorname {Pic}(Y_{e})$
. Then
$\operatorname {Pic}(Y_{e})$
. Then
![]() $\operatorname {\text {Aut}}(Y_{e}, D_{e}) / K$
acts on
$\operatorname {\text {Aut}}(Y_{e}, D_{e}) / K$
acts on
![]() $ {\operatorname {Nef}^{\; e}}(Y_{e})$
with a rational polyhedral fundamental domain.
$ {\operatorname {Nef}^{\; e}}(Y_{e})$
with a rational polyhedral fundamental domain.
Remark 5.5. The proof of Theorem 5.4 is similar to the argument of Sterk for
![]() $K3$
surfaces (see [Reference SterkS85]).
$K3$
surfaces (see [Reference SterkS85]).
Proof of Theorem 5.4.
By Theorem 5.1, the group
![]() $\operatorname {\text {Adm}}$
acts on
$\operatorname {\text {Adm}}$
acts on
![]() $ {\operatorname {Nef}^{\; e}}(Y_{gen})$
with a rational polyhedral fundamental domain. Choose a rational point
$ {\operatorname {Nef}^{\; e}}(Y_{gen})$
with a rational polyhedral fundamental domain. Choose a rational point
![]() $y \in \operatorname {Int}( {\operatorname {Nef}^{\; e}}(Y_{gen}))$
such that y has trivial stabilizer in
$y \in \operatorname {Int}( {\operatorname {Nef}^{\; e}}(Y_{gen}))$
such that y has trivial stabilizer in
![]() $\operatorname {\text {Adm}}$
. Then by [Reference LooijengaL81] Application 4.14, we obtain a rational polyhedral fundamental domain
$\operatorname {\text {Adm}}$
. Then by [Reference LooijengaL81] Application 4.14, we obtain a rational polyhedral fundamental domain
![]() $\sigma (y)$
defined as follows:
$\sigma (y)$
defined as follows:
Let
![]() $\gamma = s_{\alpha }$
, the reflection associated to a simple root
$\gamma = s_{\alpha }$
, the reflection associated to a simple root
![]() $\alpha = [C]$
where
$\alpha = [C]$
where
![]() $C \subset Y_{e} \setminus D_{e}$
is a
$C \subset Y_{e} \setminus D_{e}$
is a
![]() $(-2)$
-curve. Because
$(-2)$
-curve. Because
![]() $ s_{\alpha }(x) = x + (x \cdot \alpha ) \alpha $
, the condition
$ s_{\alpha }(x) = x + (x \cdot \alpha ) \alpha $
, the condition
is equivalent to
 $$ \begin{align*} s_{\alpha}(x) \cdot y \geq x \cdot y &\Longleftrightarrow (x + (x \cdot \alpha) \alpha) \cdot y \geq x \cdot y \\ &\Longleftrightarrow x \cdot y + (x \cdot \alpha)(\alpha \cdot y) \geq x \cdot y \\ &\Longleftrightarrow (x \cdot \alpha)(\alpha \cdot y) \geq 0. \end{align*} $$
$$ \begin{align*} s_{\alpha}(x) \cdot y \geq x \cdot y &\Longleftrightarrow (x + (x \cdot \alpha) \alpha) \cdot y \geq x \cdot y \\ &\Longleftrightarrow x \cdot y + (x \cdot \alpha)(\alpha \cdot y) \geq x \cdot y \\ &\Longleftrightarrow (x \cdot \alpha)(\alpha \cdot y) \geq 0. \end{align*} $$
Because
![]() $\alpha $
is effective and y is ample (since
$\alpha $
is effective and y is ample (since
![]() $y \in \operatorname {Int}(\operatorname {Nef}(Y_{e}))$
, which is the ample cone), the intersection
$y \in \operatorname {Int}(\operatorname {Nef}(Y_{e}))$
, which is the ample cone), the intersection
![]() $(\alpha \cdot y)$
is positive. Then
$(\alpha \cdot y)$
is positive. Then
![]() $(x \cdot \alpha )(\alpha \cdot y) \geq 0$
if and only if
$(x \cdot \alpha )(\alpha \cdot y) \geq 0$
if and only if
![]() $(x \cdot \alpha ) \geq 0$
. In particular, this shows the following:
$(x \cdot \alpha ) \geq 0$
. In particular, this shows the following:
where
![]() $\Delta $
above denotes the simple roots (see Definition 3.23), and the equality follows from the description of the nef cone in [Reference Gross, Hacking and KeelGHK15b], Lemma 2.15.
$\Delta $
above denotes the simple roots (see Definition 3.23), and the equality follows from the description of the nef cone in [Reference Gross, Hacking and KeelGHK15b], Lemma 2.15.
The following statements are true:
-
1.
 $\sigma $
is rational polyhedral ([Reference LooijengaL14], Application 4.14) and
$\sigma $
is rational polyhedral ([Reference LooijengaL14], Application 4.14) and
 $\sigma \subset {\operatorname {Nef}^{\; e}}(Y_{e})$
, as shown above;
$\sigma \subset {\operatorname {Nef}^{\; e}}(Y_{e})$
, as shown above; -
2.
 $\operatorname {\text {Adm}} = W \rtimes \operatorname {\text {Aut}}(Y_{e}, D_{e})/K$
([Reference Gross, Hacking and KeelGHK15b], Theorem 5.1 or [Reference FriedmanF15], Theorem 9.6);
$\operatorname {\text {Adm}} = W \rtimes \operatorname {\text {Aut}}(Y_{e}, D_{e})/K$
([Reference Gross, Hacking and KeelGHK15b], Theorem 5.1 or [Reference FriedmanF15], Theorem 9.6); -
3.
 $ {\operatorname {Nef}^{\; e}}(Y_{e})$
is a fundamental domain for the action of W on
$ {\operatorname {Nef}^{\; e}}(Y_{e})$
is a fundamental domain for the action of W on
 $ {\operatorname {Nef}^{\; e}}(Y_{gen})$
([Reference Gross, Hacking and KeelGHK15b], Theorem 3.2), and by the Torelli theorem ([Reference Gross, Hacking and KeelGHK15b], Theorem 1.8),
$ {\operatorname {Nef}^{\; e}}(Y_{gen})$
([Reference Gross, Hacking and KeelGHK15b], Theorem 3.2), and by the Torelli theorem ([Reference Gross, Hacking and KeelGHK15b], Theorem 1.8),
 $\operatorname {\text {Aut}}(Y_{e}, D_{e})/K \leq \operatorname {\text {Adm}}$
is the normalizer of
$\operatorname {\text {Aut}}(Y_{e}, D_{e})/K \leq \operatorname {\text {Adm}}$
is the normalizer of
 $ {\operatorname {Nef}^{\; e}}(Y_{e})$
.
$ {\operatorname {Nef}^{\; e}}(Y_{e})$
.
Next, we show how the three statements above imply that
![]() $\sigma $
is a rational polyhedral fundamental domain for the action of
$\sigma $
is a rational polyhedral fundamental domain for the action of
![]() $\operatorname {\text {Aut}}(Y_{e}, D_{e}) / K$
on
$\operatorname {\text {Aut}}(Y_{e}, D_{e}) / K$
on
![]() $ {\operatorname {Nef}^{\; e}}(Y_{e})$
. Let g be an element of
$ {\operatorname {Nef}^{\; e}}(Y_{e})$
. Let g be an element of
![]() $\operatorname {\text {Adm}}$
. By (2) above, there exist unique
$\operatorname {\text {Adm}}$
. By (2) above, there exist unique
![]() $w \in W$
and
$w \in W$
and
![]() $\theta \in \operatorname {\text {Aut}}(Y_{e}, D_{e}) / K$
such that
$\theta \in \operatorname {\text {Aut}}(Y_{e}, D_{e}) / K$
such that
![]() $g = w \theta $
. We claim that the following inclusion holds:
$g = w \theta $
. We claim that the following inclusion holds:
To see why, let
![]() $\mathcal {C}$
be the cone
$\mathcal {C}$
be the cone
which is the fundamental chamber for the action of W on
![]() $\operatorname {Pic}(Y) \otimes _{\mathbb {Z}} \mathbb {R}$
, and we have
$\operatorname {Pic}(Y) \otimes _{\mathbb {Z}} \mathbb {R}$
, and we have
![]() $\sigma \subset {\operatorname {Nef}^{\; e}}(Y_{e}) \subset \mathcal {C}$
. From above,
$\sigma \subset {\operatorname {Nef}^{\; e}}(Y_{e}) \subset \mathcal {C}$
. From above,
![]() $g = w \theta $
. Let
$g = w \theta $
. Let
![]() $x \in (g \sigma ) \; \bigcap \; {\operatorname {Nef}^{\; e}}(Y_{e})$
. The group
$x \in (g \sigma ) \; \bigcap \; {\operatorname {Nef}^{\; e}}(Y_{e})$
. The group
![]() $\operatorname {\text {Aut}}(Y_{e}, D_{e}) / K$
acts on
$\operatorname {\text {Aut}}(Y_{e}, D_{e}) / K$
acts on
![]() $ {\operatorname {Nef}^{\; e}}(Y_{e})$
. Then
$ {\operatorname {Nef}^{\; e}}(Y_{e})$
. Then
![]() $x \in \mathcal {C}$
and
$x \in \mathcal {C}$
and
![]() $x = gu = w \theta u$
, where
$x = gu = w \theta u$
, where
![]() $u \in \sigma \subset {\operatorname {Nef}^{\; e}}(Y_{e})$
and so
$u \in \sigma \subset {\operatorname {Nef}^{\; e}}(Y_{e})$
and so
![]() $\theta u \in {\operatorname {Nef}^{\; e}}(Y_{e}) \subset \mathcal {C}$
. Thus,
$\theta u \in {\operatorname {Nef}^{\; e}}(Y_{e}) \subset \mathcal {C}$
. Thus,
![]() $\theta u$
and
$\theta u$
and
![]() $w \theta u$
are in
$w \theta u$
are in
![]() $\mathcal {C}$
. So
$\mathcal {C}$
. So
![]() $\theta u \in w \mathcal {C} \; \bigcap \; \mathcal {C} \subset \operatorname {Fix}(w)$
by Sterk ([Reference SterkS85], Lemma 1.2), which means that
$\theta u \in w \mathcal {C} \; \bigcap \; \mathcal {C} \subset \operatorname {Fix}(w)$
by Sterk ([Reference SterkS85], Lemma 1.2), which means that
![]() $w \theta u = \theta u$
, i.e.,
$w \theta u = \theta u$
, i.e.,
![]() $x = \theta u$
. Then
$x = \theta u$
. Then
![]() $x = \theta u \in \theta \sigma $
, proving the inclusion 5.7.
$x = \theta u \in \theta \sigma $
, proving the inclusion 5.7.
Finally, we want to show that
![]() $\sigma $
is a rational polyhedral fundamental domain for the action of
$\sigma $
is a rational polyhedral fundamental domain for the action of
![]() $\operatorname {\text {Aut}}(Y_{e}, D_{e})/K$
on
$\operatorname {\text {Aut}}(Y_{e}, D_{e})/K$
on
![]() $ {\operatorname {Nef}^{\; e}}(Y_{e})$
. By (1),
$ {\operatorname {Nef}^{\; e}}(Y_{e})$
. By (1),
![]() $\sigma $
is rational polyhedral, so it remains to show that it is a fundamental domain. Because
$\sigma $
is rational polyhedral, so it remains to show that it is a fundamental domain. Because
![]() $\sigma $
is a fundamental domain for the action of
$\sigma $
is a fundamental domain for the action of
![]() $\operatorname {\text {Adm}}$
on
$\operatorname {\text {Adm}}$
on
![]() $ {\operatorname {Nef}^{\; e}}(Y_{gen})$
,
$ {\operatorname {Nef}^{\; e}}(Y_{gen})$
,
 $$ \begin{align*} {\operatorname{\operatorname{Nef}^{\; e}}(Y_{gen}) = \bigcup_{g \in \operatorname{\text{Adm}}} \; g \sigma}. \end{align*} $$
$$ \begin{align*} {\operatorname{\operatorname{Nef}^{\; e}}(Y_{gen}) = \bigcup_{g \in \operatorname{\text{Adm}}} \; g \sigma}. \end{align*} $$
We can write
 $$ \begin{align*} \operatorname{\operatorname{Nef}^{\; e}}(Y_{gen}) \; \bigcap \; \operatorname{\operatorname{Nef}^{\; e}}(Y_{e}) &= \bigl( \bigcup_{g \in \operatorname{\text{Adm}}} \; g \sigma \bigr) \; \cap \; \operatorname{\operatorname{Nef}^{\; e}}(Y_{e}) \\ &= \bigcup_{g \in \operatorname{\text{Adm}}} \; (g \sigma \; \cap \; \operatorname{\operatorname{Nef}^{\; e}}(Y_{e})) \\ &= \bigcup_{\theta \in \operatorname{\text{Aut}}(Y_{e}, D_{e})/K} \; \theta \sigma. \end{align*} $$
$$ \begin{align*} \operatorname{\operatorname{Nef}^{\; e}}(Y_{gen}) \; \bigcap \; \operatorname{\operatorname{Nef}^{\; e}}(Y_{e}) &= \bigl( \bigcup_{g \in \operatorname{\text{Adm}}} \; g \sigma \bigr) \; \cap \; \operatorname{\operatorname{Nef}^{\; e}}(Y_{e}) \\ &= \bigcup_{g \in \operatorname{\text{Adm}}} \; (g \sigma \; \cap \; \operatorname{\operatorname{Nef}^{\; e}}(Y_{e})) \\ &= \bigcup_{\theta \in \operatorname{\text{Aut}}(Y_{e}, D_{e})/K} \; \theta \sigma. \end{align*} $$
Here is why the last equality holds: if
![]() $g = w \theta $
, then we showed above that
$g = w \theta $
, then we showed above that
![]() $(g \sigma ) \; \bigcap \; {\operatorname {Nef}^{\; e}}(Y_{e}) \subset \theta \sigma $
. If
$(g \sigma ) \; \bigcap \; {\operatorname {Nef}^{\; e}}(Y_{e}) \subset \theta \sigma $
. If
![]() $w = 1$
, then
$w = 1$
, then
![]() $g = \theta \in \operatorname {\text {Aut}}(Y_{e}, D_{e}) / K$
and
$g = \theta \in \operatorname {\text {Aut}}(Y_{e}, D_{e}) / K$
and
because
![]() $\theta $
preserves
$\theta $
preserves
![]() $ {\operatorname {Nef}^{\; e}}(Y_{e})$
and
$ {\operatorname {Nef}^{\; e}}(Y_{e})$
and
![]() $\sigma \subset {\operatorname {Nef}^{\; e}}(Y_{e})$
. Moreover, because
$\sigma \subset {\operatorname {Nef}^{\; e}}(Y_{e})$
. Moreover, because
it follows that the same statement holds for
![]() $g_{1}, g_{2}$
in the smaller group
$g_{1}, g_{2}$
in the smaller group
![]() $\operatorname {\text {Aut}}(Y_{e}, D_{e})/K$
. That is,
$\operatorname {\text {Aut}}(Y_{e}, D_{e})/K$
. That is,
which is the second property in the definition of a fundamental domain. Therefore, we have shown, using conditions (1), (2) and (3), that
![]() $\sigma $
is a rational polyhedral fundamental domain for the action of
$\sigma $
is a rational polyhedral fundamental domain for the action of
![]() $\operatorname {\text {Aut}}(Y_{e}, D_{e})/K$
on
$\operatorname {\text {Aut}}(Y_{e}, D_{e})/K$
on
![]() $ {\operatorname {Nef}^{\; e}}(Y_{e})$
.
$ {\operatorname {Nef}^{\; e}}(Y_{e})$
.
6 New examples of Mori Dream Spaces
Theorem 6.1. A log Calabi-Yau surface
![]() $(Y_{e}, D_{e})$
with split mixed Hodge structure in which the boundary
$(Y_{e}, D_{e})$
with split mixed Hodge structure in which the boundary
![]() $D_{e}$
consists of no more than six components has a rational polyhedral cone of curves. Moreover, if the intersection matrix of
$D_{e}$
consists of no more than six components has a rational polyhedral cone of curves. Moreover, if the intersection matrix of
![]() $(D_{i}.D_{j})$
is negative definite or negative semidefinite, then the automorphism group
$(D_{i}.D_{j})$
is negative definite or negative semidefinite, then the automorphism group
![]() $\operatorname {\text {Aut}}(Y_{e}, D_{e})$
is trivial for
$\operatorname {\text {Aut}}(Y_{e}, D_{e})$
is trivial for
![]() $n=6$
(in fact, this holds for all
$n=6$
(in fact, this holds for all
![]() $n \leq 6$
). In addition, for each such surface, we give an explicit description of the cone of curves.
$n \leq 6$
). In addition, for each such surface, we give an explicit description of the cone of curves.
Corollary 6.2. A log Calabi-Yau surface
![]() $(Y_{e}, D_{e})$
with split mixed Hodge structure which has boundary
$(Y_{e}, D_{e})$
with split mixed Hodge structure which has boundary
![]() $D_{e}$
consisting of no more than six components is an example of a Mori Dream Space.
$D_{e}$
consisting of no more than six components is an example of a Mori Dream Space.
Proof. This follows from 3.1, Theorem 6.1, Theorem 4.12 and [Reference Hu and KeelHK00] Definition 1.10.
We note that Looijenga has done similar studies for the cases where
![]() $n \leq 5$
in [Reference LooijengaL81]. To keep the notation simple, we will use
$n \leq 5$
in [Reference LooijengaL81]. To keep the notation simple, we will use
![]() $(Y, D)$
to mean
$(Y, D)$
to mean
![]() $(Y_{e}, D_{e})$
from here on in this section, unless otherwise specified.
$(Y_{e}, D_{e})$
from here on in this section, unless otherwise specified.
Remark 6.3. When the cone of curves of Y has finitely many generators, it is automatically closed. Because the cones we describe below are all rational polyhedral, we have
![]() $\operatorname {{\overline{Curv}}}(Y) = \operatorname {\text {Curv}}(Y)$
.
$\operatorname {{\overline{Curv}}}(Y) = \operatorname {\text {Curv}}(Y)$
.
In this next part, we only consider log Calabi-Yau surfaces with the split mixed Hodge structure. We will show that each surface Y described for each
![]() $n \leq 6$
is the surface
$n \leq 6$
is the surface
![]() $Y_{e}$
in the given deformation type with the split mixed Hodge structure (that is, the period point
$Y_{e}$
in the given deformation type with the split mixed Hodge structure (that is, the period point
![]() $\phi $
given by
$\phi $
given by
![]() $\phi (x) = 1$
for all
$\phi (x) = 1$
for all
![]() $x \in \langle D_{1}, \dots , D_{n} \rangle _{\mathbb {Z}}^{\bot })$
.
$x \in \langle D_{1}, \dots , D_{n} \rangle _{\mathbb {Z}}^{\bot })$
.
Lemma 6.4. Let
![]() $(Y, D)$
be a log Calabi-Yau surface and suppose that
$(Y, D)$
be a log Calabi-Yau surface and suppose that
![]() $\langle D_{1}, \dots , D_{n} \rangle _{\mathbb {Z}}^{\bot }$
is generated by classes of curves
$\langle D_{1}, \dots , D_{n} \rangle _{\mathbb {Z}}^{\bot }$
is generated by classes of curves
![]() $C \subset Y \setminus D$
. Then
$C \subset Y \setminus D$
. Then
![]() $\phi (x) = 1$
for all
$\phi (x) = 1$
for all
![]() $x \in \langle D_{1}, \dots , D_{n} \rangle _{\mathbb {Z}}^{\bot }$
.
$x \in \langle D_{1}, \dots , D_{n} \rangle _{\mathbb {Z}}^{\bot }$
.
Proof. Using the notation
![]() $\theta : \operatorname {Pic}^{0}(D) \xrightarrow {\sim } \mathbb {C}^{\ast }$
from Definition 3.20, we recall that
$\theta : \operatorname {Pic}^{0}(D) \xrightarrow {\sim } \mathbb {C}^{\ast }$
from Definition 3.20, we recall that
![]() $\phi ([C]) = \theta (\mathcal {O}_{Y}(C) \vert _{D})$
. Because
$\phi ([C]) = \theta (\mathcal {O}_{Y}(C) \vert _{D})$
. Because
![]() $C \bigcap D = \emptyset $
, the restriction
$C \bigcap D = \emptyset $
, the restriction
![]() $\mathcal {O}_{Y}(C) \vert _{D} = \mathcal {O}_{D}$
is the trivial line bundle on D. Then
$\mathcal {O}_{Y}(C) \vert _{D} = \mathcal {O}_{D}$
is the trivial line bundle on D. Then
![]() $\phi ([C]) = 1$
. From our assumption, it follows that
$\phi ([C]) = 1$
. From our assumption, it follows that
![]() $\phi (x) = 1$
for all
$\phi (x) = 1$
for all
![]() $x \in \langle D_{1}, \dots , D_{n} \rangle _{\mathbb {Z}}^{\bot }$
.
$x \in \langle D_{1}, \dots , D_{n} \rangle _{\mathbb {Z}}^{\bot }$
.
The lemma applies in our situation because for the surfaces we describe in cases
![]() $n \leq 6$
, the lattice
$n \leq 6$
, the lattice
![]() $\langle D_{1}, \dots , D_{n} \rangle _{\mathbb {Z}}^{\bot }$
is generated by the classes of
$\langle D_{1}, \dots , D_{n} \rangle _{\mathbb {Z}}^{\bot }$
is generated by the classes of
![]() $(-2)$
-curves C in
$(-2)$
-curves C in
![]() $Y \setminus D$
.
$Y \setminus D$
.
Remark 6.5. We cover every deformation type for each
![]() $n \leq 6$
of log Calabi-Yau surfaces such that the intersection matrix
$n \leq 6$
of log Calabi-Yau surfaces such that the intersection matrix
![]() $(D_{i} \cdot D_{j})$
is negative definite or negative semidefinite. This follows from results of Looijenga for
$(D_{i} \cdot D_{j})$
is negative definite or negative semidefinite. This follows from results of Looijenga for
![]() $n \leq 5$
([Reference LooijengaL81]) and Simonetti for
$n \leq 5$
([Reference LooijengaL81]) and Simonetti for
![]() $n = 6$
([Reference SimonettiS21]).
$n = 6$
([Reference SimonettiS21]).
Remark 6.6. If the intersection matrix
![]() $(D_{i} \cdot D_{j})$
is not negative definite nor negative semidefinite, then
$(D_{i} \cdot D_{j})$
is not negative definite nor negative semidefinite, then
![]() $\operatorname {Nef}(Y)$
is rational polyhedral by the Cone Theorem ([Reference Gross, Hacking and KeelGHK15a], Lemma 6.9).
$\operatorname {Nef}(Y)$
is rational polyhedral by the Cone Theorem ([Reference Gross, Hacking and KeelGHK15a], Lemma 6.9).
Here we prove the statement of Theorem 6.1 about
![]() $\operatorname {{\overline{Curv}}}(Y_{e})$
being rational polyhedral for
$\operatorname {{\overline{Curv}}}(Y_{e})$
being rational polyhedral for
![]() $n \leq 6$
. To do this, we consider separately the six cases
$n \leq 6$
. To do this, we consider separately the six cases
![]() $n=1, \dots , 6$
and use Lemma 6.7 below. We note that in each of the cases considered, the number of boundary components remains the same. Here, we refer to Theorem 1.1 in [Reference LooijengaL81], which gives the description of
$n=1, \dots , 6$
and use Lemma 6.7 below. We note that in each of the cases considered, the number of boundary components remains the same. Here, we refer to Theorem 1.1 in [Reference LooijengaL81], which gives the description of
![]() $\bar {Y}$
and
$\bar {Y}$
and
![]() $\bar {D}$
in each of the cases
$\bar {D}$
in each of the cases
![]() $n \leq 5$
. The general blowup picture can be described as follows: the boundary D is a cycle of components
$n \leq 5$
. The general blowup picture can be described as follows: the boundary D is a cycle of components
![]() $D_{i}$
, where
$D_{i}$
, where
![]() $i = 1, \dots , n$
, and each boundary component is linked to a ‘chain’ of a single
$i = 1, \dots , n$
, and each boundary component is linked to a ‘chain’ of a single
![]() $(-1)$
-curve followed by arbitrarily many
$(-1)$
-curve followed by arbitrarily many
![]() $(-2)$
-curves.
$(-2)$
-curves.
For all cases
![]() $n = 1, \dots , 6$
, we denote the exceptional curves by
$n = 1, \dots , 6$
, we denote the exceptional curves by
![]() $E_{i, j}$
, where
$E_{i, j}$
, where
![]() $E_{i, 1}$
is the unique
$E_{i, 1}$
is the unique
![]() $(-1)$
-curve in the chain intersecting the boundary component
$(-1)$
-curve in the chain intersecting the boundary component
![]() $D_{i}$
at one point q, and j ranges from
$D_{i}$
at one point q, and j ranges from
![]() $1$
to the total number of blowups at q.
$1$
to the total number of blowups at q.
Lemma 6.7. Let Y be a smooth projective complex surface. Let
![]() $\mathcal {B}$
be a basis for
$\mathcal {B}$
be a basis for
![]() $N_{1}(Y)$
consisting of irreducible curves. Suppose the dual basis may be expressed as effective combinations of a set
$N_{1}(Y)$
consisting of irreducible curves. Suppose the dual basis may be expressed as effective combinations of a set
![]() $\mathcal {C}$
of curves. Then
$\mathcal {C}$
of curves. Then
![]() $\operatorname {\text {Curv}}(Y) = \langle \mathcal {B} \; \cup \; \mathcal {C} \rangle _{\mathbb {R} \geq 0}$
.
$\operatorname {\text {Curv}}(Y) = \langle \mathcal {B} \; \cup \; \mathcal {C} \rangle _{\mathbb {R} \geq 0}$
.
Proof. Let
![]() $C \subset Y$
be a curve and suppose that
$C \subset Y$
be a curve and suppose that
![]() $C \notin \mathcal {B}$
. Then
$C \notin \mathcal {B}$
. Then
![]() $C \cdot B_{i} \geq 0$
for all
$C \cdot B_{i} \geq 0$
for all
![]() $B_{i} \in \mathcal {B}$
. Since
$B_{i} \in \mathcal {B}$
. Since
![]() $B_{i}^{\ast }$
is an effective linear combination of elements in
$B_{i}^{\ast }$
is an effective linear combination of elements in
![]() $\mathcal {C}$
and
$\mathcal {C}$
and
![]() $C \cdot B_{i} \geq 0$
, it follows that
$C \cdot B_{i} \geq 0$
, it follows that
![]() $C = \sum (C \cdot B_{i}) B_{i}^{\ast }$
belongs to
$C = \sum (C \cdot B_{i}) B_{i}^{\ast }$
belongs to
![]() $\langle \; \mathcal {C} \; \rangle _{\mathbb {R}_{\geq 0}}$
.
$\langle \; \mathcal {C} \; \rangle _{\mathbb {R}_{\geq 0}}$
.
Number of boundary components
 $n=1$
.
$n=1$
.
Let
![]() $\bar {Y} = \mathbb {P}^{2}$
with a rational nodal curve
$\bar {Y} = \mathbb {P}^{2}$
with a rational nodal curve
![]() $\bar {D}_{1}$
and a flex point q. In coordinates, we may take
$\bar {D}_{1}$
and a flex point q. In coordinates, we may take
We denote the tangent line at point q by
![]() $\bar {F}$
, and we blow up the point q some number
$\bar {F}$
, and we blow up the point q some number
![]() $p_{1}$
of times. This results in chain of exceptional curves with self-intersections
$p_{1}$
of times. This results in chain of exceptional curves with self-intersections
![]() $-1, -2, \dots , -2, -2, -2$
. We label these curves by
$-1, -2, \dots , -2, -2, -2$
. We label these curves by
![]() $E_{1, 1}, E_{1, 2}, \dots , E_{1, p_{1}-2}, E_{1, p_{1}-1}, E_{1, p_{1}}$
. The curve
$E_{1, 1}, E_{1, 2}, \dots , E_{1, p_{1}-2}, E_{1, p_{1}-1}, E_{1, p_{1}}$
. The curve
![]() $E_{1, p_{1}-2}$
intersects a
$E_{1, p_{1}-2}$
intersects a
![]() $(-2)$
-curve F at one point. A basis for
$(-2)$
-curve F at one point. A basis for
![]() $\operatorname {Pic}(Y)$
is
$\operatorname {Pic}(Y)$
is
and its dual basis
![]() $\mathcal {B}^{\ast }_{1}$
consists of the following elements:
$\mathcal {B}^{\ast }_{1}$
consists of the following elements:
 $$ \begin{align*} E_{1, p_{1}}^{\ast} &= D_{1} \\ E_{1, p_{1}-1}^{\ast} &= D_{1} + E_{1, p_{1}} \\ E_{1, p_{1}-2}^{\ast} &= D_{1} + 2E_{1, p_{1}} + E_{1, p_{1}-1} \\ E_{1, p_{1}-3}^{\ast} &= D_{1} + 3E_{1, p_{1}} + 2E_{1, p_{1}-1} + E_{1, p_{1}-2} \\ \vdots \\ E_{1, j}^{\ast} &= D_{1} + (p_{1} - j) E_{1, p_{1}} + (p_{1} - j - 1)E_{1, p_{1}-1} + \cdots + 2E_{1, j+2} + E_{1, {j+1}} \; \text{ for } 3 \leq j \leq p_{1}; \end{align*} $$
$$ \begin{align*} E_{1, p_{1}}^{\ast} &= D_{1} \\ E_{1, p_{1}-1}^{\ast} &= D_{1} + E_{1, p_{1}} \\ E_{1, p_{1}-2}^{\ast} &= D_{1} + 2E_{1, p_{1}} + E_{1, p_{1}-1} \\ E_{1, p_{1}-3}^{\ast} &= D_{1} + 3E_{1, p_{1}} + 2E_{1, p_{1}-1} + E_{1, p_{1}-2} \\ \vdots \\ E_{1, j}^{\ast} &= D_{1} + (p_{1} - j) E_{1, p_{1}} + (p_{1} - j - 1)E_{1, p_{1}-1} + \cdots + 2E_{1, j+2} + E_{1, {j+1}} \; \text{ for } 3 \leq j \leq p_{1}; \end{align*} $$
and
 $$ \begin{align*} E_{1, 2}^{\ast} &= 4E_{1, p_{1}} + 4E_{1, p_{1}-1} + \cdots + 4E_{1, 4} + 4E_{1, 3} + 2E_{1, 2} + E_{1,1} + 2F \\ E_{1, 1}^{\ast} &= 2E_{1, p_{1}} + 2E_{1, p_{1}-1} + \cdots + 2E_{1, 4} + 2E_{1, 3} + E_{1, 2} + F \\ F^{\ast} &= 3E_{1, p_{1}} + 3E_{1, p_{1}-1} + \cdots + 3E_{1, 4} + 3E_{1, 3} + 2E_{1, 2} + E_{1, 1} + F. \end{align*} $$
$$ \begin{align*} E_{1, 2}^{\ast} &= 4E_{1, p_{1}} + 4E_{1, p_{1}-1} + \cdots + 4E_{1, 4} + 4E_{1, 3} + 2E_{1, 2} + E_{1,1} + 2F \\ E_{1, 1}^{\ast} &= 2E_{1, p_{1}} + 2E_{1, p_{1}-1} + \cdots + 2E_{1, 4} + 2E_{1, 3} + E_{1, 2} + F \\ F^{\ast} &= 3E_{1, p_{1}} + 3E_{1, p_{1}-1} + \cdots + 3E_{1, 4} + 3E_{1, 3} + 2E_{1, 2} + E_{1, 1} + F. \end{align*} $$
By Lemma 6.7, we can describe the cone of curves as follows:
Remark 6.8. The formulas above can be obtained in the following way. Here, we use the notation
and we label the maps by
![]() $\pi _{i}: Y_{i} \rightarrow Y_{i-1}$
. We let
$\pi _{i}: Y_{i} \rightarrow Y_{i-1}$
. We let
![]() $D = D_{m} \subset Y_{m} = Y$
and
$D = D_{m} \subset Y_{m} = Y$
and
![]() $\bar {D} = D_{0} \subset \bar {Y} = Y_{0}$
, and
$\bar {D} = D_{0} \subset \bar {Y} = Y_{0}$
, and
![]() $D_{i} \subset Y_{i}$
for
$D_{i} \subset Y_{i}$
for
![]() $i = 1, \dots m-1$
. Let
$i = 1, \dots m-1$
. Let
![]() $f = \pi _{1} \circ \pi _{2} \circ \dots \circ \pi _{m}$
and let
$f = \pi _{1} \circ \pi _{2} \circ \dots \circ \pi _{m}$
and let
![]() $f_{i}: Y \rightarrow Y_{i}$
be the map
$f_{i}: Y \rightarrow Y_{i}$
be the map
![]() $f_{i} := \pi _{i} \circ \dots \circ \pi _{m}$
. Since there is only one component of D in this case (
$f_{i} := \pi _{i} \circ \dots \circ \pi _{m}$
. Since there is only one component of D in this case (
![]() $n=1$
so
$n=1$
so
![]() $D = D_{1}$
), instead of writing
$D = D_{1}$
), instead of writing
![]() $E_{1, j}$
, for simplicity we will just keep track of the second subscript and write
$E_{1, j}$
, for simplicity we will just keep track of the second subscript and write
![]() $E_{j}$
. Then,
$E_{j}$
. Then,
so that
![]() $E_{i}^{\ast } \cdot E_{j} = \delta _{ij}$
. In addition, if we let
$E_{i}^{\ast } \cdot E_{j} = \delta _{ij}$
. In addition, if we let
![]() $F^{\ast } := \pi ^{\ast }(H)$
, where H is a hyperplane class on
$F^{\ast } := \pi ^{\ast }(H)$
, where H is a hyperplane class on
![]() $\mathbb {P}^{2}$
and
$\mathbb {P}^{2}$
and
![]() $\pi $
is the composition of maps
$\pi $
is the composition of maps
![]() $\pi _{i}$
, then
$\pi _{i}$
, then
![]() $F^{\ast } \cdot E_{i} = 0$
and
$F^{\ast } \cdot E_{i} = 0$
and
![]() $F^{\ast } \cdot F = 1$
. This deriviation results in the same expressions as listed above, and we omit similar arguments which give the expressions of dual basis elements for the remaining n values.
$F^{\ast } \cdot F = 1$
. This deriviation results in the same expressions as listed above, and we omit similar arguments which give the expressions of dual basis elements for the remaining n values.
Number of boundary components
 $n=2$
.
$n=2$
.
Let
![]() $\bar {Y}$
be the Hirzebruch surface
$\bar {Y}$
be the Hirzebruch surface
![]() $\mathbb {F}_{2}$
with two smooth curves
$\mathbb {F}_{2}$
with two smooth curves
![]() $\bar {D}_{1}$
and
$\bar {D}_{1}$
and
![]() $\bar {D}_{2}$
in the linear system
$\bar {D}_{2}$
in the linear system
![]() $\vert B + 2A \vert $
. Here, B denotes the negative section of the
$\vert B + 2A \vert $
. Here, B denotes the negative section of the
![]() $\mathbb {P}^{1}$
fibration
$\mathbb {P}^{1}$
fibration
![]() $\mathbb {F}_{2} \rightarrow \mathbb {P}^{1}$
, and A denotes the fiber. We may assume that the curves
$\mathbb {F}_{2} \rightarrow \mathbb {P}^{1}$
, and A denotes the fiber. We may assume that the curves
![]() $\bar {D}_{1}$
and
$\bar {D}_{1}$
and
![]() $\bar {D}_{2}$
intersect transversely. We fix two points
$\bar {D}_{2}$
intersect transversely. We fix two points
![]() $q_{i} \in \bar {D}_{i}$
where
$q_{i} \in \bar {D}_{i}$
where
![]() $i = 1, 2$
, such that the points lie on a common fiber
$i = 1, 2$
, such that the points lie on a common fiber
![]() $\bar {F}_{1}$
, and let
$\bar {F}_{1}$
, and let
![]() $\bar {F}_{2}$
be the second
$\bar {F}_{2}$
be the second
![]() $(-2)$
-curve meeting
$(-2)$
-curve meeting
![]() $\bar {F}_{1}$
at a single point. Then blow up at the points
$\bar {F}_{1}$
at a single point. Then blow up at the points
![]() $q_{i}$
some number of times (say we blow up a total of
$q_{i}$
some number of times (say we blow up a total of
![]() $p_{i}$
times at points
$p_{i}$
times at points
![]() $q_{i}$
for
$q_{i}$
for
![]() $i = 1, 2$
). The curves
$i = 1, 2$
). The curves
![]() $F_{i}$
are the strict transforms of
$F_{i}$
are the strict transforms of
![]() $\bar {F}_{i}$
for
$\bar {F}_{i}$
for
![]() $i = 1, 2$
.
$i = 1, 2$
.
A basis
![]() $\mathcal {B}_{2}$
for
$\mathcal {B}_{2}$
for
![]() $\operatorname {Pic}(Y)$
is given by
$\operatorname {Pic}(Y)$
is given by
The dual basis
![]() $\mathcal {B}^{\ast }_{2}$
consists of the following elements:
$\mathcal {B}^{\ast }_{2}$
consists of the following elements:
where for
![]() $i = 1, 2$
,
$i = 1, 2$
,
 $$ \begin{align*} E_{i, p_{i}}^{\ast} &= D_{i} \\ E_{i, p_{i} - 1}^{\ast} &= D_{i} + E_{i, p_{i}} \\ E_{i, p_{i} - 2}^{\ast} &= D_{i} + 2E_{i, p_{i}} + E_{i, p_{i} - 1} \\ &\vdots \\ E_{i, 1}^{\ast} &= D_{i} + (p_{i}-1) E_{i, p_{i}} + (p_{i} - 2) E_{i, p_{i}-1} + \cdots + 2E_{i, 3} + E_{i, 2} \end{align*} $$
$$ \begin{align*} E_{i, p_{i}}^{\ast} &= D_{i} \\ E_{i, p_{i} - 1}^{\ast} &= D_{i} + E_{i, p_{i}} \\ E_{i, p_{i} - 2}^{\ast} &= D_{i} + 2E_{i, p_{i}} + E_{i, p_{i} - 1} \\ &\vdots \\ E_{i, 1}^{\ast} &= D_{i} + (p_{i}-1) E_{i, p_{i}} + (p_{i} - 2) E_{i, p_{i}-1} + \cdots + 2E_{i, 3} + E_{i, 2} \end{align*} $$
and
and
By Lemma 6.7, we can describe the cone of curves as follows:
Number of boundary components
 $n=3$
.
$n=3$
.
Let
![]() $\bar {Y} = \mathbb {P}^{2}$
with
$\bar {Y} = \mathbb {P}^{2}$
with
![]() $\bar {D} = \bar {D}_{1} + \bar {D}_{2} + \bar {D}_{3}$
its toric boundary, which is the union of three lines. Fix three collinear points
$\bar {D} = \bar {D}_{1} + \bar {D}_{2} + \bar {D}_{3}$
its toric boundary, which is the union of three lines. Fix three collinear points
![]() $q_{i} \in \bar {D}_{i}$
where
$q_{i} \in \bar {D}_{i}$
where
![]() $i = 1, 2, 3$
and blow them up some number of times. Let F be the strict transform of the line
$i = 1, 2, 3$
and blow them up some number of times. Let F be the strict transform of the line
![]() $\bar {F}$
passing through the three points of blowup, one on each component
$\bar {F}$
passing through the three points of blowup, one on each component
![]() $\bar {D}_{i}$
.
$\bar {D}_{i}$
.
A basis
![]() $\mathcal {B}_{3}$
for
$\mathcal {B}_{3}$
for
![]() $\operatorname {Pic}(Y)$
is given by
$\operatorname {Pic}(Y)$
is given by
The dual basis
![]() $\mathcal {B}^{\ast }_{3}$
consists of the elements, for
$\mathcal {B}^{\ast }_{3}$
consists of the elements, for
![]() $i = 1, 2, 3$
:
$i = 1, 2, 3$
:
 $$ \begin{align*} E_{i, p_{i}}^{\ast} &= D_{i} \\ E_{i, p_{i} - 1}^{\ast} &= D_{i} + E_{i, p_{i}} \\ E_{i, p_{i} - 2}^{\ast} &= D_{i} + 2E_{i, p_{i}} + E_{i, p_{i} - 1} \\ &\vdots \\ E_{i, 1}^{\ast} &= D_{i} + (p_{i}-1)E_{i, p_{i}} + (p_{i} - 2)E_{i, p_{i}-1} + \cdots + 2E_{i, 3} + E_{i, 2} \end{align*} $$
$$ \begin{align*} E_{i, p_{i}}^{\ast} &= D_{i} \\ E_{i, p_{i} - 1}^{\ast} &= D_{i} + E_{i, p_{i}} \\ E_{i, p_{i} - 2}^{\ast} &= D_{i} + 2E_{i, p_{i}} + E_{i, p_{i} - 1} \\ &\vdots \\ E_{i, 1}^{\ast} &= D_{i} + (p_{i}-1)E_{i, p_{i}} + (p_{i} - 2)E_{i, p_{i}-1} + \cdots + 2E_{i, 3} + E_{i, 2} \end{align*} $$
and
By Lemma 6.7, we can describe the cone of curves as follows:
Number of boundary components
 $n=4$
.
$n=4$
.
Let
![]() $\bar {Y} = \mathbb {P}^{1} \times \mathbb {P}^{1}$
with its toric boundary, which is the union of two fibers of each of the two projections
$\bar {Y} = \mathbb {P}^{1} \times \mathbb {P}^{1}$
with its toric boundary, which is the union of two fibers of each of the two projections
![]() $\mathbb {P}^{1} \times \mathbb {P}^{1} \rightarrow \mathbb {P}^{1}$
. Fix four points
$\mathbb {P}^{1} \times \mathbb {P}^{1} \rightarrow \mathbb {P}^{1}$
. Fix four points
![]() $q_{i} \in \bar {D}_{i}$
where
$q_{i} \in \bar {D}_{i}$
where
![]() $i = 1, \dots , 4$
such that
$i = 1, \dots , 4$
such that
![]() $q_{1}$
and
$q_{1}$
and
![]() $q_{3}$
lie on a fiber
$q_{3}$
lie on a fiber
![]() $\bar {F}_{1}$
of the first projection and
$\bar {F}_{1}$
of the first projection and
![]() $q_{2}$
and
$q_{2}$
and
![]() $q_{4}$
lie on a fiber
$q_{4}$
lie on a fiber
![]() $\bar {F}_{2}$
of the second projection. Then blow them up some number of times.
$\bar {F}_{2}$
of the second projection. Then blow them up some number of times.
A basis for
![]() $\operatorname {Pic}(Y)$
is
$\operatorname {Pic}(Y)$
is
The dual basis
![]() $\mathcal {B}^{\ast }_{4}$
consists of the following elements:
$\mathcal {B}^{\ast }_{4}$
consists of the following elements:
 $$ \begin{align*} E_{i, p_{i}}^{\ast} &= D_{i} \\ E_{i, p_{i}-1}^{\ast} &= D_{i} + E_{i, p_{i}} \\ E_{i, p_{i}-2}^{\ast} &= D_{i} + 2E_{i, p_{i}} + E_{i, p_{i} - 1} \\ &\vdots \\ E_{i, 1}^{\ast} &= D_{i} + (p_{i}-1) E_{i, p_{i}} + (p_{i} - 2) E_{i, p_{i}-1} + \cdots + 2E_{i, 3} + E_{i, 2}, \end{align*} $$
$$ \begin{align*} E_{i, p_{i}}^{\ast} &= D_{i} \\ E_{i, p_{i}-1}^{\ast} &= D_{i} + E_{i, p_{i}} \\ E_{i, p_{i}-2}^{\ast} &= D_{i} + 2E_{i, p_{i}} + E_{i, p_{i} - 1} \\ &\vdots \\ E_{i, 1}^{\ast} &= D_{i} + (p_{i}-1) E_{i, p_{i}} + (p_{i} - 2) E_{i, p_{i}-1} + \cdots + 2E_{i, 3} + E_{i, 2}, \end{align*} $$
and for each of
![]() $F_{j}$
where
$F_{j}$
where
![]() $j = 1, 2$
, there are two (linearly equivalent) possibilities:
$j = 1, 2$
, there are two (linearly equivalent) possibilities:
with
![]() $i= 2$
or
$i= 2$
or
![]() $4$
for
$4$
for
![]() $j=1$
and
$j=1$
and
![]() $i=1$
or
$i=1$
or
![]() $3$
for
$3$
for
![]() $j=2$
. By Lemma 6.7, we can describe the cone of curves as follows:
$j=2$
. By Lemma 6.7, we can describe the cone of curves as follows:
Number of boundary components
 $n=5$
.
$n=5$
.
Let
![]() $\bar {Y}$
be the blowup of four points in general position in
$\bar {Y}$
be the blowup of four points in general position in
![]() $\mathbb {P}^{2}$
and let
$\mathbb {P}^{2}$
and let
![]() $\bar {D}$
be a cycle of five
$\bar {D}$
be a cycle of five
![]() $(-1)$
-curves. The surface
$(-1)$
-curves. The surface
![]() $\bar {Y}$
contains ten
$\bar {Y}$
contains ten
![]() $(-1)$
-curves:
$(-1)$
-curves:
-
1. Four are exceptional curves
 $E_{i}$
from blowing up the points
$E_{i}$
from blowing up the points
 $p_{i}$
, for
$p_{i}$
, for
 $i = 1, 2, 3, 4$
.
$i = 1, 2, 3, 4$
. -
2. Six (obtained by 6 =
 $4 \choose 2$
) are strict transforms
$4 \choose 2$
) are strict transforms
 $l^{\prime }_{ij}$
of lines
$l^{\prime }_{ij}$
of lines
 $l_{ij}$
defined by points
$l_{ij}$
defined by points
 $p_{i}$
and
$p_{i}$
and
 $p_{j}$
.
$p_{j}$
.
The process of blowing up points
![]() $p_{i}$
for
$p_{i}$
for
![]() $i=1, \dots , 4$
on
$i=1, \dots , 4$
on
![]() $\mathbb {P}^{2}$
to obtain a surface with ten curves is shown in Figure 6.1. Taking the dual of this figure (see Figure 6.2), we choose a pentagon inside and rearrange vertices so that this pentagon encloses all other vertices. Then the interior vertices can be rearranged to form a star, resulting in the Petersen graph. The dual of the interior five-pointed star is a pentagon, and the dual of the outside pentagonal boundary is again a pentagon. Together, these two parts form the configuration of
$\mathbb {P}^{2}$
to obtain a surface with ten curves is shown in Figure 6.1. Taking the dual of this figure (see Figure 6.2), we choose a pentagon inside and rearrange vertices so that this pentagon encloses all other vertices. Then the interior vertices can be rearranged to form a star, resulting in the Petersen graph. The dual of the interior five-pointed star is a pentagon, and the dual of the outside pentagonal boundary is again a pentagon. Together, these two parts form the configuration of
![]() $(-1)$
-curves on the surface
$(-1)$
-curves on the surface
![]() $\bar {Y}$
. The
$\bar {Y}$
. The
![]() $\bar {F}_{i}$
’s are
$\bar {F}_{i}$
’s are
![]() $(-1)$
-curves not contained in the boundary in
$(-1)$
-curves not contained in the boundary in
![]() $\bar {Y}$
; the
$\bar {Y}$
; the
![]() $\bar {F}_{i}$
’s correspond to a pentagonal star. Each
$\bar {F}_{i}$
’s correspond to a pentagonal star. Each
![]() $\bar {F}_{i}$
intersects the boundary component
$\bar {F}_{i}$
intersects the boundary component
![]() $\bar {D}_{i}$
, and we denote their strict transforms by
$\bar {D}_{i}$
, and we denote their strict transforms by
![]() $F_{i}$
.
$F_{i}$
.

Figure 6.1 Blowing up once at each point
![]() $p_{1}, \dots , p_{4}$
results in the diagram above.
$p_{1}, \dots , p_{4}$
results in the diagram above.

Figure 6.2 The dual graph of the blowup shown in Figure 6.1 is drawn on the left, and it is equivalent to the Petersen graph shown on the right.
The remaining
![]() $(-1)$
-curves on
$(-1)$
-curves on
![]() $\bar {Y}$
intersect
$\bar {Y}$
intersect
![]() $\bar {D}$
transversely in five points
$\bar {D}$
transversely in five points
![]() $q_{i}$
where
$q_{i}$
where
![]() $i = 1, \dots , 5$
. Blow up these points some number of times to obtain Figure 6.3. A basis
$i = 1, \dots , 5$
. Blow up these points some number of times to obtain Figure 6.3. A basis
![]() $\mathcal {B}_{5}$
for
$\mathcal {B}_{5}$
for
![]() $\operatorname {Pic}(Y)$
is the collection
$\operatorname {Pic}(Y)$
is the collection

Figure 6.3 Blowing up once at each point
![]() $q_{1}, \dots , q_{5}$
results in the diagram above.
$q_{1}, \dots , q_{5}$
results in the diagram above.
The dual elements
![]() $E_{i, j}^{\ast }$
and
$E_{i, j}^{\ast }$
and
![]() $F_{i}$
, where
$F_{i}$
, where
![]() $1 \leq i \leq 5$
and
$1 \leq i \leq 5$
and
![]() $1 \leq j \leq p_{i}$
, are defined as follows:
$1 \leq j \leq p_{i}$
, are defined as follows:
 $$ \begin{align*} E_{i, p_{i}}^{\ast} &= D_{i} \\ E_{i, p_{i}-1}^{\ast} &= D_{i} + E_{i, p_{i}} \\ E_{i, p_{i}-2}^{\ast} &= D_{i} + 2E_{i, p_{i}} + E_{i, p_{i}-1} \\ & \vdots \\ E_{i, 1}^{\ast} &= D_{i} + (p_{i}-1) E_{i, p_{i}} + (p_{i} - 2) E_{i, p_{i}-1} + \cdots + 2E_{i, 3} + E_{i, 2} \\ F_{i}^{\ast} &= D_{i} + p_{i}E_{i, p_{i}} + (p_{i}-1)E_{i, p_{i}-1} + \cdots + 2E_{i, 2} + E_{i,1}. \end{align*} $$
$$ \begin{align*} E_{i, p_{i}}^{\ast} &= D_{i} \\ E_{i, p_{i}-1}^{\ast} &= D_{i} + E_{i, p_{i}} \\ E_{i, p_{i}-2}^{\ast} &= D_{i} + 2E_{i, p_{i}} + E_{i, p_{i}-1} \\ & \vdots \\ E_{i, 1}^{\ast} &= D_{i} + (p_{i}-1) E_{i, p_{i}} + (p_{i} - 2) E_{i, p_{i}-1} + \cdots + 2E_{i, 3} + E_{i, 2} \\ F_{i}^{\ast} &= D_{i} + p_{i}E_{i, p_{i}} + (p_{i}-1)E_{i, p_{i}-1} + \cdots + 2E_{i, 2} + E_{i,1}. \end{align*} $$
By Lemma 6.7, we can describe the cone of curves as follows:
Number of boundary components
 $n=6$
.
$n=6$
.
In this case, by [Reference SimonettiS21],
![]() $(Y, D)$
is obtained as a blowup of the toric surface
$(Y, D)$
is obtained as a blowup of the toric surface
![]() $\bar {Y}$
with toric boundary
$\bar {Y}$
with toric boundary
![]() $\bar {D} = \bar {D}_{1} + \cdots + \bar {D}_{6}$
, a hexagon of
$\bar {D} = \bar {D}_{1} + \cdots + \bar {D}_{6}$
, a hexagon of
![]() $(-1)$
-curves (shown in Figure 6.4). Take
$(-1)$
-curves (shown in Figure 6.4). Take
![]() $q_{i}$
where
$q_{i}$
where
![]() $i = 1 \dots , 6$
to be the points
$i = 1 \dots , 6$
to be the points
![]() $(-1) \in \mathbb {C}^{\ast } \subset \mathbb {P}^{1} = \bar {D}_{i}$
for some choice of toric coordinates on
$(-1) \in \mathbb {C}^{\ast } \subset \mathbb {P}^{1} = \bar {D}_{i}$
for some choice of toric coordinates on
![]() $\bar {Y}$
, and Y the blowup of
$\bar {Y}$
, and Y the blowup of
![]() $\bar {Y}$
some number of times at each
$\bar {Y}$
some number of times at each
![]() $q_{i}$
. Define an index set as follows:
$q_{i}$
. Define an index set as follows:
Let
![]() $F_{k}$
be the strict transform of
$F_{k}$
be the strict transform of
![]() $\bar {F}_{k}$
on Y. We consider the following five curves
$\bar {F}_{k}$
on Y. We consider the following five curves
![]() $\bar {F}_{k}$
on
$\bar {F}_{k}$
on
![]() $\bar {Y}$
(
$\bar {Y}$
(
![]() $k \in K$
), such that
$k \in K$
), such that
![]() $\bar {F}_{k} \cap \bar {D} = \{q_{i} \; \vert \; i \in k\}$
.
$\bar {F}_{k} \cap \bar {D} = \{q_{i} \; \vert \; i \in k\}$
.
-
1.
 $\bar {F}_{1, 3, 5}$
and
$\bar {F}_{1, 3, 5}$
and
 $\bar {F}_{2, 4, 6}$
are pullbacks of a line in
$\bar {F}_{2, 4, 6}$
are pullbacks of a line in
 $\mathbb {P}^{2}$
for two different birational morphisms
$\mathbb {P}^{2}$
for two different birational morphisms
 $\bar {Y} \rightarrow \mathbb {P}^{2}$
; and
$\bar {Y} \rightarrow \mathbb {P}^{2}$
; and -
2.
 $\bar {F}_{1, 4}$
and
$\bar {F}_{1, 4}$
and
 $\bar {F}_{2, 5}$
and
$\bar {F}_{2, 5}$
and
 $\bar {F}_{3, 6}$
are fibers of three different morphisms
$\bar {F}_{3, 6}$
are fibers of three different morphisms
 $\bar {Y} \rightarrow \mathbb {P}^{1}$
.
$\bar {Y} \rightarrow \mathbb {P}^{1}$
.

Figure 6.4 This diagram shows the surface
![]() $(\bar {Y}, \bar {D})$
blown up at points
$(\bar {Y}, \bar {D})$
blown up at points
![]() $q_{i}$
, each a total of
$q_{i}$
, each a total of
![]() $p_{i}$
times, for when
$p_{i}$
times, for when
![]() $n = 6$
.
$n = 6$
.
The classes of the curves
![]() $\{\bar {F}_{k}\}$
span
$\{\bar {F}_{k}\}$
span
![]() $\operatorname {Pic}(\bar {Y})$
with one relation:
$\operatorname {Pic}(\bar {Y})$
with one relation:
For
![]() $i = 1, \dots , 6$
and
$i = 1, \dots , 6$
and
![]() $j = 0, \dots , p_{i}$
, define a divisor
$j = 0, \dots , p_{i}$
, define a divisor
Then for
![]() $j> 0$
, we have
$j> 0$
, we have
 $$ \begin{align} A_{i, j} \cdot E_{s, t} =\left\{ \begin{array}{@{}ll@{}} 1 & \text{if } i = s \text{ and } j=t; \\ 0 & \text{otherwise.} \end{array}\right. \end{align} $$
$$ \begin{align} A_{i, j} \cdot E_{s, t} =\left\{ \begin{array}{@{}ll@{}} 1 & \text{if } i = s \text{ and } j=t; \\ 0 & \text{otherwise.} \end{array}\right. \end{align} $$
The set
![]() $S = \{E_{i, j} \; \vert \; i = 1, \dots , 6\} \cup \{F_{k} \; \vert \; k \in K\}$
spans
$S = \{E_{i, j} \; \vert \; i = 1, \dots , 6\} \cup \{F_{k} \; \vert \; k \in K\}$
spans
![]() $\operatorname {Pic}(Y)$
because the set
$\operatorname {Pic}(Y)$
because the set
![]() $\{\bar {F}_{k} \; \vert \; k \in K\}$
spans
$\{\bar {F}_{k} \; \vert \; k \in K\}$
spans
![]() $\operatorname {Pic}(\bar {Y})$
.
$\operatorname {Pic}(\bar {Y})$
.
Let
![]() $C \subset Y$
be an irreducible curve. Suppose that
$C \subset Y$
be an irreducible curve. Suppose that
![]() $C \neq D_{i} ,E_{i, j}$
for all
$C \neq D_{i} ,E_{i, j}$
for all
![]() $i, j$
. Then
$i, j$
. Then
![]() $C \cdot A_{i, j} \geq 0$
for all
$C \cdot A_{i, j} \geq 0$
for all
![]() $i, j$
. We can write
$i, j$
. We can write
Computing the intersection numbers
![]() $A_{i, j} \cdot E_{s, t}$
and
$A_{i, j} \cdot E_{s, t}$
and
![]() $A_{i, j} \cdot F_{k}$
results in the following inequalities:
$A_{i, j} \cdot F_{k}$
results in the following inequalities:
 $$ \begin{align*} a_{i, j} &\geq 0 \text{ for all } i, j; \\ b_{1, 4} &+ b_{1, 3, 5} \geq 0; \\ b_{1, 4} &+ b_{2, 4, 6} \geq 0; \\ b_{2, 5} &+ b_{1, 3, 5} \geq 0; \\ b_{2, 5} &+ b_{2, 4, 6} \geq 0; \\ b_{3, 6} &+ b_{1, 3, 5} \geq 0; \text{ and } \\ b_{3, 6} &+ b_{2, 4, 6} \geq 0; \end{align*} $$
$$ \begin{align*} a_{i, j} &\geq 0 \text{ for all } i, j; \\ b_{1, 4} &+ b_{1, 3, 5} \geq 0; \\ b_{1, 4} &+ b_{2, 4, 6} \geq 0; \\ b_{2, 5} &+ b_{1, 3, 5} \geq 0; \\ b_{2, 5} &+ b_{2, 4, 6} \geq 0; \\ b_{3, 6} &+ b_{1, 3, 5} \geq 0; \text{ and } \\ b_{3, 6} &+ b_{2, 4, 6} \geq 0; \end{align*} $$
The last six inequalities define the cone
where
![]() $V := \langle [F_{k}] \; \vert \; k \in K \rangle _{\mathbb {R}}$
. Using the spanning set
$V := \langle [F_{k}] \; \vert \; k \in K \rangle _{\mathbb {R}}$
. Using the spanning set
of V, we can identify
![]() $\sigma $
with the cone
$\sigma $
with the cone
Then, we may assume that
![]() $b_{k} \geq 0$
for all
$b_{k} \geq 0$
for all
![]() $k \in K$
, so that C lies in the cone generated by the
$k \in K$
, so that C lies in the cone generated by the
![]() $E_{i, j}$
and the
$E_{i, j}$
and the
![]() $F_{k}$
. Therefore,
$F_{k}$
. Therefore,
![]() $\operatorname {{\overline{Curv}}}(Y) = \langle D_{i}, E_{i, j}, F_{k} \; \vert \; i = 1, \dots , 6 \text { and } j = 1, \dots , p_{i} \text { and } k \in K \rangle _{\mathbb {R}_{\geq 0}}$
.
$\operatorname {{\overline{Curv}}}(Y) = \langle D_{i}, E_{i, j}, F_{k} \; \vert \; i = 1, \dots , 6 \text { and } j = 1, \dots , p_{i} \text { and } k \in K \rangle _{\mathbb {R}_{\geq 0}}$
.
To finish the proof of Theorem 6.1, we first explain why
![]() $\operatorname {\text {Aut}}(Y, D)$
is trivial for
$\operatorname {\text {Aut}}(Y, D)$
is trivial for
![]() $n = 6$
. We note that the cases where
$n = 6$
. We note that the cases where
![]() $n \leq 5$
is shown by Looijenga in [Reference LooijengaL81]. Consider the case where
$n \leq 5$
is shown by Looijenga in [Reference LooijengaL81]. Consider the case where
![]() $n = 6$
. We denote by
$n = 6$
. We denote by
![]() $(\bar {Y}, \bar {D})$
the toric pair (a log Calabi-Yau surface where
$(\bar {Y}, \bar {D})$
the toric pair (a log Calabi-Yau surface where
![]() $\bar {Y}$
is a toric surface and
$\bar {Y}$
is a toric surface and
![]() $\bar {D}$
its toric boundary) and
$\bar {D}$
its toric boundary) and
![]() $(Y, D)$
is the blowup of
$(Y, D)$
is the blowup of
![]() $(\bar {Y}, \bar {D})$
. Here, D is either negative definite or negative semidefinite, and D does not contain any
$(\bar {Y}, \bar {D})$
. Here, D is either negative definite or negative semidefinite, and D does not contain any
![]() $(-1)$
-curves. We note that
$(-1)$
-curves. We note that
![]() $\operatorname {\text {Aut}}(\bar {Y}, \bar {D}) \cong (\mathbb {C}^{\ast })^{2}$
. Moreover,
$\operatorname {\text {Aut}}(\bar {Y}, \bar {D}) \cong (\mathbb {C}^{\ast })^{2}$
. Moreover,
![]() $\operatorname {\text {Aut}}(Y, D) \subset \operatorname {\text {Aut}}(\bar {Y}, \bar {D})$
: this is because there exists a unique chain consisting of a single
$\operatorname {\text {Aut}}(Y, D) \subset \operatorname {\text {Aut}}(\bar {Y}, \bar {D})$
: this is because there exists a unique chain consisting of a single
![]() $(-1)$
-curve (which intersects a boundary component), and the
$(-1)$
-curve (which intersects a boundary component), and the
![]() $(-1)$
-curve intersects a chain of
$(-1)$
-curve intersects a chain of
![]() $(-2)$
-curves (which are disjoint from the boundary). In fact, the list of
$(-2)$
-curves (which are disjoint from the boundary). In fact, the list of
![]() $(-2)$
-curves in
$(-2)$
-curves in
![]() $Y \setminus D$
and
$Y \setminus D$
and
![]() $(-1)$
-curve in Y (not contained in D but intersecting D at a single point) is complete. This follows from the description of
$(-1)$
-curve in Y (not contained in D but intersecting D at a single point) is complete. This follows from the description of
![]() $\operatorname {{\overline{Curv}}}(Y)$
using Lemma 6.7. To be more precise, if S is a surface and
$\operatorname {{\overline{Curv}}}(Y)$
using Lemma 6.7. To be more precise, if S is a surface and
![]() $C \subset S$
a curve with
$C \subset S$
a curve with
![]() $C^{2} < 0$
, then C is an extremal ray of
$C^{2} < 0$
, then C is an extremal ray of
![]() $\operatorname {{\overline{Curv}}}(Y)$
. Thus, any
$\operatorname {{\overline{Curv}}}(Y)$
. Thus, any
![]() $(-1)$
or
$(-1)$
or
![]() $(-2)$
-curve is an extremal ray. Above, we have the list of generators of
$(-2)$
-curve is an extremal ray. Above, we have the list of generators of
![]() $\operatorname {{\overline{Curv}}}(Y)$
for
$\operatorname {{\overline{Curv}}}(Y)$
for
![]() $n = 6$
, so any
$n = 6$
, so any
![]() $(-1)$
or
$(-1)$
or
![]() $(-2)$
-curve must be one of those generators. Any automorphism of
$(-2)$
-curve must be one of those generators. Any automorphism of
![]() $(Y, D)$
will permute this unique chain of
$(Y, D)$
will permute this unique chain of
![]() $(-1)$
and
$(-1)$
and
![]() $(-2)$
-curves, and in particular, it must fix the unique
$(-2)$
-curves, and in particular, it must fix the unique
![]() $(-1)$
-curve in this chain. The image must fix the points which are blown up because it fixes the exceptional divisors which are mapped to it. By a short affine coordinates computation, it follows that
$(-1)$
-curve in this chain. The image must fix the points which are blown up because it fixes the exceptional divisors which are mapped to it. By a short affine coordinates computation, it follows that
![]() $\operatorname {\text {Aut}}(Y, D)$
is trivial.
$\operatorname {\text {Aut}}(Y, D)$
is trivial.
Acknowledgements
This paper is mostly based on results from my PhD thesis. I am grateful to my advisor, Paul Hacking, for his guidance on this project. I thank Ben Heidenreich, Eyal Markman, Jenia Tevelev and Burt Totaro for their insightful comments and suggestions. I thank Alejandro Morales, John Ottem, Luca Schaffler, Angelica Simonetti and Sebastian Torres for useful discussions. I also thank the referee for helpful suggestions.
Data availability statement
Replication data and code can be found in Harvard Dataverse: https://doi.org/link.
Ethical standards
The research meets all ethical guidelines, including adherence to the legal requirements of the study country.
Author contributions
A.A. and A.B.C. designed the study, abstracted the data wrote the first draft, and approved the final version of the manuscript. A.R.E.J., M.R.L., K.L.S. and A.D.P. revised the manuscript and approved the final version.
Competing interest
The authors have no competing interest to declare.
Financial support
This research was partially supported by the NSF grant (DMS-1901970).