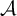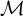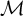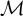1 Introduction
The notion of torsion pairs was introduced for arbitrary abelian categories in [Reference DicksonD] to generalise the properties of the class of torsion groups in the category of abelian groups. Since then, torsion theories, and the related notion of t-structures [Reference Beĭlinson, Bernstein and DeligneBBD] for triangulated categories, have become ubiquitous in representation theory, homological algebra and algebraic geometry. Within these areas, torsion theories and t-structures play a key role in topics such as (perverse) sheaves [Reference Beĭlinson, Bernstein and DeligneBBD], tilting theory and its generalisations [Reference Brenner and ButlerBB, Reference Adachi, Iyama and ReitenAIR, Reference Angeleri Hügel, Marks and VitóriaAHMV, Reference Angeleri Hügel, Laking, Šťovíček and VitóriaAHLSV], and stability conditions [Reference BridgelandB].
Meanwhile, higher homological algebra has become an increasingly active field of research since its introduction in [Reference IyamaI1, Reference IyamaI2, Reference IyamaI3]. It has found applications in algebraic K-theory [Reference Dyckerhoff, Jasso and WaldeDJW], wrapped Floer theory in symplectic geometry [Reference Dyckerhoff, Jasso and LekiliDJL], and in algebraic geometry where it was an important ingredient in the proof of the Donovan-Wemyss conjecture [Reference Jasso, Keller and MuroJKM]. Originally motivated by Auslander–Reiten theory, cluster tilting theory and the classical Auslander correspondence, one studies categories where the role of short exact sequences (or distinguished triangles) is taken by longer sequences. Examples include d-abelian and d-exact categories [Reference JassoJ2],
![]() $(d+2)$
-angulated categories [Reference Geiss, Keller and OppermannGKO] and d-exangulated categories [Reference Herschend, Liu and NakaokaHLN1]. Here, the positive integer d controls the length of the important sequences, with
$(d+2)$
-angulated categories [Reference Geiss, Keller and OppermannGKO] and d-exangulated categories [Reference Herschend, Liu and NakaokaHLN1]. Here, the positive integer d controls the length of the important sequences, with
![]() $d=1$
coinciding with the classical cases.
$d=1$
coinciding with the classical cases.
By work of [Reference JassoJ2, Reference KvammeKv, Reference Ebrahimi and Nasr-IsfahaniEN-I], studying d-abelian categories is equivalent to studying so-called d-cluster tilting subcategories of abelian categories. Our setup will be the latter, where we assume the ambient abelian category to be of finite length (see Section 2.1 for details). Many important classical concepts in representation theory generalise to this setting. In this paper, we focus on the higher analogue of torsion classes – namely, d-torsion classes – introduced in [Reference JørgensenJø] and further studied in [Reference Asadollahi, Jørgensen, Schroll and TreffingerAJST].
A fundamental result in the study of torsion classes states that a subcategory of an abelian length category is a torsion class if and only if it is closed under extensions and quotients [Reference DicksonD]. This result is of crucial importance, as it both allows for the detection of torsion classes and, moreover, gives properties which play a key role in many proofs related to these objects. A higher-dimensional version of this classical characterisation would hence be a substantial advancement. The main result of this paper gives such a characterisation of d-torsion classes in terms of closure under d-extensions and d-quotients (see Definitions 3.6 and 3.7). Note that throughout this paper, we assume subcategories to be closed under finite direct sums and summands; see the subsection on conventions and notation below.
Theorem 1.1 (Theorem 3.17).
Let
![]() $\mathcal {M}$
be a d-cluster tilting subcategory of an abelian length category
$\mathcal {M}$
be a d-cluster tilting subcategory of an abelian length category
![]() $\mathcal {A}$
. A subcategory of
$\mathcal {A}$
. A subcategory of
![]() $\mathcal {M}$
is a d-torsion class if and only if it is closed under d-extensions and d-quotients.
$\mathcal {M}$
is a d-torsion class if and only if it is closed under d-extensions and d-quotients.
Note that while a different characterisation of d-torsion classes using the bounded derived category of
![]() $\mathcal {A}$
has been given in the special case where
$\mathcal {A}$
has been given in the special case where
![]() $\mathcal {A}$
is the module category of a d-representation finite d-hereditary algebra [Reference JørgensenJø], the characterisation in Theorem 1.1 works generally, does not require use of derived categories and is closer to the classical result for torsion classes.
$\mathcal {A}$
is the module category of a d-representation finite d-hereditary algebra [Reference JørgensenJø], the characterisation in Theorem 1.1 works generally, does not require use of derived categories and is closer to the classical result for torsion classes.
The proof of Theorem 1.1 makes significant use of the main result in [Reference Asadollahi, Jørgensen, Schroll and TreffingerAJST], which relates d-torsion classes in
![]() $\mathcal {M}$
to torsion classes in
$\mathcal {M}$
to torsion classes in
![]() $\mathcal {A}$
. This allows us to apply results about torsion classes also in the higher setup. As another key ingredient in the proof of Theorem 1.1, we give a higher generalisation of the classical factorisation of a morphism in an abelian category as the composition of an epimorphism followed by a monomorphism; see Proposition 3.13. This result is of independent interest, and we expect it to play a role in providing answers to other questions in higher homological algebra.
$\mathcal {A}$
. This allows us to apply results about torsion classes also in the higher setup. As another key ingredient in the proof of Theorem 1.1, we give a higher generalisation of the classical factorisation of a morphism in an abelian category as the composition of an epimorphism followed by a monomorphism; see Proposition 3.13. This result is of independent interest, and we expect it to play a role in providing answers to other questions in higher homological algebra.
With Theorem 1.1 in hand, we are able to generalise other well-known results about torsion classes to the higher setting. For example, an immediate consequence of combining Theorem 1.1 with a result in [Reference KlapprothKl] is that every d-torsion class carries the structure of a d-exact category; see Corollary 3.19.
Other important results concerning classical torsion classes include the study of their poset structure. The set
![]() $\operatorname {tors}(\mathcal {A})$
of torsion classes in
$\operatorname {tors}(\mathcal {A})$
of torsion classes in
![]() $\mathcal {A}$
has a natural partial order given by inclusion, and this poset is actually a complete lattice, with meet given by intersection; see, for example, [Reference Iyama, Reiten, Thomas and TodorovIRTT, Proposition 2.3]. Theorem 1.1 allows us to give the following generalisation of this result.
$\mathcal {A}$
has a natural partial order given by inclusion, and this poset is actually a complete lattice, with meet given by intersection; see, for example, [Reference Iyama, Reiten, Thomas and TodorovIRTT, Proposition 2.3]. Theorem 1.1 allows us to give the following generalisation of this result.
Theorem 1.2 (Theorem 4.3).
Let
![]() $\mathcal {M}$
be a d-cluster tilting subcategory of an abelian length category
$\mathcal {M}$
be a d-cluster tilting subcategory of an abelian length category
![]() $\mathcal {A}$
. Then the set
$\mathcal {A}$
. Then the set
![]() $d\text {-}\!\operatorname {tors}(\mathcal {M})$
of all d-torsion classes in
$d\text {-}\!\operatorname {tors}(\mathcal {M})$
of all d-torsion classes in
![]() $\mathcal {M}$
is a complete lattice with meet given by intersection.
$\mathcal {M}$
is a complete lattice with meet given by intersection.
In the classical setting, lattice-theoretic properties of
![]() $\operatorname {tors}(\mathcal {A})$
form an area of active research [Reference Asai and PfeifferAP, Reference Garver and McConvilleGM, Reference JassoJ1], which is intimately related to representation theory [Reference Barnard, Carrol and ZhuBCZ, Reference Demonet, Iyama, Reading, Reiten and ThomasDIRRT]. We refer to [Reference ThomasT] for an introductory survey on the topic. Theorem 1.2 opens up a new avenue of research in higher homological algebra through the study of the lattice of higher torsion classes.
$\operatorname {tors}(\mathcal {A})$
form an area of active research [Reference Asai and PfeifferAP, Reference Garver and McConvilleGM, Reference JassoJ1], which is intimately related to representation theory [Reference Barnard, Carrol and ZhuBCZ, Reference Demonet, Iyama, Reading, Reiten and ThomasDIRRT]. We refer to [Reference ThomasT] for an introductory survey on the topic. Theorem 1.2 opens up a new avenue of research in higher homological algebra through the study of the lattice of higher torsion classes.
The classical characterisation of torsion classes as those subcategories that are closed under extensions and quotients is often used to determine if a given subcategory is a torsion class or to compute the smallest torsion class containing that given subcategory. Crucial to the success of this approach is that we often have a good understanding of the middle terms in extensions. To use Theorem 1.1 in an analogous way to determine d-torsion classes, we therefore need an understanding of the middle terms in d-extensions, which is notably more complicated. The following result simplifies this problem significantly.
Theorem 1.3 (Theorem 3.20).
Let
![]() $\mathcal {M}$
be a d-cluster tilting subcategory of an abelian length category
$\mathcal {M}$
be a d-cluster tilting subcategory of an abelian length category
![]() $\mathcal {A}$
. Suppose
$\mathcal {A}$
. Suppose
![]() $\mathcal {U} \subseteq \mathcal {M}$
is closed under under d-extensions with indecomposable end terms and all d-quotients. Then
$\mathcal {U} \subseteq \mathcal {M}$
is closed under under d-extensions with indecomposable end terms and all d-quotients. Then
![]() $\mathcal {U}$
is closed under all d-extensions.
$\mathcal {U}$
is closed under all d-extensions.
This theorem is of independent interest, as extension closure is a useful concept across many areas of representation theory. In this paper, we focus on using Theorem 1.3 to classify d-torsion classes in concrete examples.
We apply our results to higher Auslander algebras of type
![]() $\mathbb {A}$
[Reference IyamaI3] and higher Nakayama algebras of type
$\mathbb {A}$
[Reference IyamaI3] and higher Nakayama algebras of type
![]() $\mathbb {A}$
and
$\mathbb {A}$
and
![]() $\mathbb {A}_\infty ^\infty $
[Reference Jasso, Külshammer, Psaroudakis and KvammeJKPK]. The module category of each such algebra contains a d-cluster tilting subcategory, and their combinatorial descriptions due to [Reference Oppermann and ThomasOT] and [Reference Jasso, Külshammer, Psaroudakis and KvammeJKPK] make them an ideal testing ground for new results in higher homological algebra. Higher Auslander algebras are particularly important, as their derived categories are equivalent to certain partially wrapped Fukaya categories [Reference Dyckerhoff, Jasso and LekiliDJL]. We use Theorems 1.1 and 1.3 to give a combinatorial description of all d-torsion classes associated to these algebras, where the classification results for the three families are given in Theorems 5.13, 6.1 and 6.5, respectively. Moreover, we implement our results in algorithms that compute and count all d-torsion classes; see Table 2 and Remark 6.3.
$\mathbb {A}_\infty ^\infty $
[Reference Jasso, Külshammer, Psaroudakis and KvammeJKPK]. The module category of each such algebra contains a d-cluster tilting subcategory, and their combinatorial descriptions due to [Reference Oppermann and ThomasOT] and [Reference Jasso, Külshammer, Psaroudakis and KvammeJKPK] make them an ideal testing ground for new results in higher homological algebra. Higher Auslander algebras are particularly important, as their derived categories are equivalent to certain partially wrapped Fukaya categories [Reference Dyckerhoff, Jasso and LekiliDJL]. We use Theorems 1.1 and 1.3 to give a combinatorial description of all d-torsion classes associated to these algebras, where the classification results for the three families are given in Theorems 5.13, 6.1 and 6.5, respectively. Moreover, we implement our results in algorithms that compute and count all d-torsion classes; see Table 2 and Remark 6.3.
We expect that the results we present in this article will provide tools for any further study of d-torsion classes and will be of importance in building bridges between d-torsion classes and other subjects in representation theory and beyond. This is demonstrated in a forthcoming paper [Reference August, Haugland, Jacobsen, Kvamme, Palu and TreffingerAHJ+], where Theorem 1.1 is applied to establish a connection between functorially finite d-torsion classes,
![]() $\tau _d$
-tilting theory and
$\tau _d$
-tilting theory and
![]() $(d+1)$
-term silting objects.
$(d+1)$
-term silting objects.
Structure of the paper
In Section 2, we give an overview of the definitions and background used in the rest of the paper. In Section 3, we prove Theorems 1.1 and 1.3, while Theorem 1.2 is shown in Section 4. Section 5 is dedicated to the study of d-torsion classes associated to higher Auslander algebras. Finally, we extend our view to higher Nakayama algebras in Section 6.
Conventions and notation
Throughout this paper, let d denote a positive integer and
![]() $\mathcal {A}$
an essentially small abelian category. We always assume
$\mathcal {A}$
an essentially small abelian category. We always assume
![]() $\mathcal {A}$
to be a finite length category, which implies that the Krull–Remak–Schmidt property is satisfied; see [Reference KrauseKr, Lemma 5.1 and Theorem 5.5].
$\mathcal {A}$
to be a finite length category, which implies that the Krull–Remak–Schmidt property is satisfied; see [Reference KrauseKr, Lemma 5.1 and Theorem 5.5].
We let
![]() $\mathbb {k}$
be a field. Given a finite-dimensional
$\mathbb {k}$
be a field. Given a finite-dimensional
![]() $\mathbb {k}$
-algebra A, the notation
$\mathbb {k}$
-algebra A, the notation
![]() $\operatorname {mod}A$
is used for the category of finitely presented right A-modules.
$\operatorname {mod}A$
is used for the category of finitely presented right A-modules.
Arrows in a quiver are composed from left to right, meaning that we write
![]() $ab$
for the path starting in the source of a and ending in the target of b.
$ab$
for the path starting in the source of a and ending in the target of b.
All subcategories are assumed to be full and closed under isomorphisms and finite direct sums. They are also assumed to be closed under direct summands. For a collection of objects
![]() $\mathcal {X}$
in an additive category
$\mathcal {X}$
in an additive category
![]() $\mathcal {C}$
, we denote by
$\mathcal {C}$
, we denote by
![]() $\operatorname {add}(\mathcal {X})$
the smallest subcategory of
$\operatorname {add}(\mathcal {X})$
the smallest subcategory of
![]() $\mathcal {C}$
which contains
$\mathcal {C}$
which contains
![]() $\mathcal {X}$
and is closed under finite direct sums and direct summands.
$\mathcal {X}$
and is closed under finite direct sums and direct summands.
2 Background and preliminaries
In this section, we provide an overview of definitions and results which give the foundation for the rest of the paper. Before we start discussing notions from higher homological algebra, we recall some terminology related to subcategories and approximations.
Let
![]() $\mathcal {X}$
be a subcategory of the abelian category
$\mathcal {X}$
be a subcategory of the abelian category
![]() $\mathcal {A}$
. We say that
$\mathcal {A}$
. We say that
![]() $\mathcal {X}$
is generating if any object in
$\mathcal {X}$
is generating if any object in
![]() $\mathcal {A}$
is a quotient of an object in
$\mathcal {A}$
is a quotient of an object in
![]() $\mathcal {X}$
; that is, for every
$\mathcal {X}$
; that is, for every
![]() $Y \in \mathcal {A}$
, there exists an exact sequence
$Y \in \mathcal {A}$
, there exists an exact sequence
![]() $X \to Y \to 0$
with
$X \to Y \to 0$
with
![]() $X \in \mathcal {X}$
. Dually, we can define the notion of cogenerating, and we call a subcategory generating-cogenerating if it is both generating and cogenerating.
$X \in \mathcal {X}$
. Dually, we can define the notion of cogenerating, and we call a subcategory generating-cogenerating if it is both generating and cogenerating.
Given an object
![]() $Y \in \mathcal {A}$
, a morphism
$Y \in \mathcal {A}$
, a morphism
![]() $f \colon Y \rightarrow X$
with
$f \colon Y \rightarrow X$
with
![]() $X\in \mathcal {X}$
is a left
$X\in \mathcal {X}$
is a left
![]() $\mathcal {X}$
-approximation of Y if any morphism
$\mathcal {X}$
-approximation of Y if any morphism
![]() $Y \rightarrow X'$
with
$Y \rightarrow X'$
with
![]() $X'\in \mathcal {X}$
factors through f. The subcategory
$X'\in \mathcal {X}$
factors through f. The subcategory
![]() $\mathcal {X}$
is called covariantly finite if every object in
$\mathcal {X}$
is called covariantly finite if every object in
![]() $\mathcal {A}$
admits a left
$\mathcal {A}$
admits a left
![]() $\mathcal {X}$
-approximation. The notions of right
$\mathcal {X}$
-approximation. The notions of right
![]() $\mathcal {X}$
-approximations and contravariantly finite subcategories are defined dually, and a subcategory is functorially finite if it is both covariantly and contravariantly finite.
$\mathcal {X}$
-approximations and contravariantly finite subcategories are defined dually, and a subcategory is functorially finite if it is both covariantly and contravariantly finite.
Recall that a morphism
![]() $f \colon X \rightarrow Y$
is called left minimal if any endomorphism g of Y satisfying
$f \colon X \rightarrow Y$
is called left minimal if any endomorphism g of Y satisfying
![]() $g \circ f = f$
is an isomorphism. A minimal left
$g \circ f = f$
is an isomorphism. A minimal left
![]() $\mathcal {X}$
-approximation is a left
$\mathcal {X}$
-approximation is a left
![]() $\mathcal {X}$
-approximation which is also left minimal. Right minimal morphisms and minimal right
$\mathcal {X}$
-approximation which is also left minimal. Right minimal morphisms and minimal right
![]() $\mathcal {X}$
-approximations are defined dually. Since
$\mathcal {X}$
-approximations are defined dually. Since
![]() $\mathcal {A}$
is Krull–Schmidt, an object has a left (right)
$\mathcal {A}$
is Krull–Schmidt, an object has a left (right)
![]() $\mathcal {X}$
-approximation if and only if it has a minimal left (right)
$\mathcal {X}$
-approximation if and only if it has a minimal left (right)
![]() $\mathcal {X}$
-approximation ([Reference Krause and SaorínKS, Corollary 1.4]).
$\mathcal {X}$
-approximation ([Reference Krause and SaorínKS, Corollary 1.4]).
2.1 d-cluster tilting subcategories and d-abelian categories
The theory of higher homological algebra originated in [Reference IyamaI1, Reference IyamaI2] with the study of d-cluster tilting subcategories. The definition is given below.
Definition 2.1. A functorially finite generating-cogenerating subcategory
![]() $\mathcal {M}$
of the abelian category
$\mathcal {M}$
of the abelian category
![]() $\mathcal {A}$
is d-cluster tilting if
$\mathcal {A}$
is d-cluster tilting if
 $$ \begin{align*} \mathcal{M} &= \{X \in \mathcal{A} \mid \operatorname{Ext}_{\mathcal{A}}^i(X,M)=0 \text{ for}\ M \in \mathcal{M}\ \text{and}\ i = 1,\ldots, d-1\}\\ &= \{Y \in \mathcal{A} \mid \operatorname{Ext}_{\mathcal{A}}^i(M,Y)=0 \text{ for}\ M \in \mathcal{M}\ \text{and}\ i = 1,\ldots, d-1\}. \end{align*} $$
$$ \begin{align*} \mathcal{M} &= \{X \in \mathcal{A} \mid \operatorname{Ext}_{\mathcal{A}}^i(X,M)=0 \text{ for}\ M \in \mathcal{M}\ \text{and}\ i = 1,\ldots, d-1\}\\ &= \{Y \in \mathcal{A} \mid \operatorname{Ext}_{\mathcal{A}}^i(M,Y)=0 \text{ for}\ M \in \mathcal{M}\ \text{and}\ i = 1,\ldots, d-1\}. \end{align*} $$
To formalise the homological structure of d-cluster tilting subcategories, Jasso introduced d-abelian categories, where the case
![]() $d=1$
recovers the classical notion of abelian categories [Reference JassoJ2]. To give a precise definition, we first recall some terminology.
$d=1$
recovers the classical notion of abelian categories [Reference JassoJ2]. To give a precise definition, we first recall some terminology.
Let
![]() $\mathcal {M}$
be an additive category and recall that a weak cokernel of a morphism
$\mathcal {M}$
be an additive category and recall that a weak cokernel of a morphism
![]() $f \colon X \to Y$
in
$f \colon X \to Y$
in
![]() $\mathcal {M}$
is a morphism
$\mathcal {M}$
is a morphism
![]() $g\colon Y \to Z$
in
$g\colon Y \to Z$
in
![]() $\mathcal {M}$
for which the induced sequence
$\mathcal {M}$
for which the induced sequence
is exact for any
![]() $M\in \mathcal {M}$
. This is equivalent to saying that
$M\in \mathcal {M}$
. This is equivalent to saying that
![]() $g \circ f = 0$
and that for any
$g \circ f = 0$
and that for any
![]() $g'\colon Y \to M$
with
$g'\colon Y \to M$
with
![]() $g' \circ f = 0$
, there exists a (not necessarily unique) morphism
$g' \circ f = 0$
, there exists a (not necessarily unique) morphism
![]() $h \colon Z \to M$
such that
$h \colon Z \to M$
such that
![]() $h \circ g = g'$
. We call a morphism g a weak cokernel if there exists a morphism f such that g is a weak cokernel of f.
$h \circ g = g'$
. We call a morphism g a weak cokernel if there exists a morphism f such that g is a weak cokernel of f.
A d-cokernel of a morphism
![]() $f_0\colon X_0 \to X_1$
in
$f_0\colon X_0 \to X_1$
in
![]() $\mathcal {M}$
is given by a sequence of morphisms
$\mathcal {M}$
is given by a sequence of morphisms
in
![]() $\mathcal {M}$
such that for every M in
$\mathcal {M}$
such that for every M in
![]() $\mathcal {M}$
, the sequence
$\mathcal {M}$
, the sequence
of abelian groups is exact. Such a d-cokernel is sometimes simply denoted by
![]() $(f_1, \dots , f_{d})$
, and
$(f_1, \dots , f_{d})$
, and
![]() $(f_1, \dots , f_{d})$
is a d-cokernel of
$(f_1, \dots , f_{d})$
is a d-cokernel of
![]() $f_0$
if and only if
$f_0$
if and only if
![]() $f_i$
is a weak cokernel of
$f_i$
is a weak cokernel of
![]() $f_{i-1}$
for
$f_{i-1}$
for
![]() $i= 1,\ldots , d-1$
and
$i= 1,\ldots , d-1$
and
![]() $f_d$
is the cokernel of
$f_d$
is the cokernel of
![]() $f_{d-1}$
. The notion of a d-kernel in
$f_{d-1}$
. The notion of a d-kernel in
![]() $\mathcal {M}$
is defined dually. A sequence
$\mathcal {M}$
is defined dually. A sequence
in
![]() $\mathcal {M}$
is called a d-exact sequence or a d-extension if
$\mathcal {M}$
is called a d-exact sequence or a d-extension if
![]() $(f_1, \dots , f_{d})$
is a d-cokernel of
$(f_1, \dots , f_{d})$
is a d-cokernel of
![]() $f_0$
and
$f_0$
and
![]() $(f_0, \dots , f_{d-1})$
is a d-kernel of
$(f_0, \dots , f_{d-1})$
is a d-kernel of
![]() $f_d$
.
$f_d$
.
Definition 2.2 [Reference JassoJ2, Definition 3.1].
An additive category
![]() $\mathcal {M}$
is d-abelian if it is idempotent complete, every morphism admits a d-kernel and a d-cokernel, and every monomorphism
$\mathcal {M}$
is d-abelian if it is idempotent complete, every morphism admits a d-kernel and a d-cokernel, and every monomorphism
![]() $f_0$
(resp. epimorphism
$f_0$
(resp. epimorphism
![]() $f_d$
) fits into a d-exact sequence of the form (1).
$f_d$
) fits into a d-exact sequence of the form (1).
A d-exact sequence of the form (1) is said to be equivalent to a d-exact sequence
if there exists a commutative diagram

Note that this defines an equivalence relation on the class of d-exact sequences whenever the category
![]() $\mathcal {M}$
is d-abelian [Reference JassoJ2, Proposition 4.10].
$\mathcal {M}$
is d-abelian [Reference JassoJ2, Proposition 4.10].
When
![]() $\mathcal {M}\subseteq \mathcal {A}$
is a d-cluster tilting subcategory, d-exact sequences coincide precisely with exact sequences of the form (1) where all terms are in
$\mathcal {M}\subseteq \mathcal {A}$
is a d-cluster tilting subcategory, d-exact sequences coincide precisely with exact sequences of the form (1) where all terms are in
![]() $\mathcal {M}$
. Moreover, any exact sequence in
$\mathcal {M}$
. Moreover, any exact sequence in
![]() $\mathcal {A}$
of the form (1) with end terms in
$\mathcal {A}$
of the form (1) with end terms in
![]() $\mathcal {M}$
is equivalent to one where all terms are in
$\mathcal {M}$
is equivalent to one where all terms are in
![]() $\mathcal {M}$
[Reference IyamaI1, A.1].
$\mathcal {M}$
[Reference IyamaI1, A.1].
In a d-abelian category, we also find higher analogues of the classical notions of pushouts and pullbacks. For more details on the construction of d-pushouts and d-pullbacks, we refer the reader to [Reference JassoJ2, Section 2.3].
Jasso proved the following theorem, which shows that d-abelian categories capture the homological structure of d-cluster tilting subcategories.
Theorem 2.3 [Reference JassoJ2, Theorem 3.16].
Let
![]() $\mathcal {M}$
be a d-cluster tilting subcategory of
$\mathcal {M}$
be a d-cluster tilting subcategory of
![]() $\mathcal {A}$
. Then
$\mathcal {A}$
. Then
![]() $\mathcal {M}$
is d-abelian.
$\mathcal {M}$
is d-abelian.
It has recently been shown that the converse of Theorem 2.3 also holds, i.e., that any d-abelian category is equivalent to a d-cluster tilting subcategory of an abelian category [Reference Ebrahimi and Nasr-IsfahaniEN-I, Reference KvammeKv]. Therefore, all d-abelian categories may be treated as d-cluster tilting subcategories.
We end this subsection by introducing a running example that will help us illustrate many of the results in this paper.
Example 2.4 Consider the quiver
![]() $1 \xrightarrow{\alpha} 2 \xrightarrow{\beta} 3 $
. Let A denote the path algebra of this quiver modulo the ideal generated by the relation
$1 \xrightarrow{\alpha} 2 \xrightarrow{\beta} 3 $
. Let A denote the path algebra of this quiver modulo the ideal generated by the relation
![]() $\alpha \beta $
. Figure 1 shows the Auslander–Reiten quiver of
$\alpha \beta $
. Figure 1 shows the Auslander–Reiten quiver of
![]() $\operatorname {mod}A$
, where the dashed arrows indicate the Auslander–Reiten translation. The subcategory
$\operatorname {mod}A$
, where the dashed arrows indicate the Auslander–Reiten translation. The subcategory
is
![]() $2$
-cluster tilting in
$2$
-cluster tilting in
![]() $\operatorname {mod}A$
, and
$\operatorname {mod}A$
, and
![]() $\mathcal {M}$
is hence an example of a
$\mathcal {M}$
is hence an example of a
![]() $2$
-abelian category. The indecomposable objects of
$2$
-abelian category. The indecomposable objects of
![]() $\operatorname {mod}A$
that generate
$\operatorname {mod}A$
that generate
![]() $\mathcal {M}$
are marked in Figure 1.
$\mathcal {M}$
are marked in Figure 1.

Figure 1 The Auslander–Reiten quiver of the module category considered in Example 2.4, with the generators of the
![]() $2$
-cluster tilting subcategory
$2$
-cluster tilting subcategory
![]() $\mathcal {M}$
marked.
$\mathcal {M}$
marked.
2.2 Minimality
The d-kernels and d-cokernels in a d-abelian category are unique only up to homotopy. Many of our proofs require a stronger sense of uniqueness, which is why we recall the concept of minimality in this section.
The Jacobson radical of the abelian category
![]() $\mathcal {A}$
consists of the morphisms
$\mathcal {A}$
consists of the morphisms
For more details and basic properties, see [Reference Assem, Simson and SkowrońskiASS, A.3].
Definition 2.5 [Reference Herschend and JørgensenHJ, Definition 2.5].
Let
![]() $\mathcal {M}$
be a d-cluster tilting subcategory of
$\mathcal {M}$
be a d-cluster tilting subcategory of
![]() $\mathcal {A}$
.
$\mathcal {A}$
.
-
(1) A d-cokernel
of a morphism $$\begin{align*}X_1 \xrightarrow{f_1} X_2 \xrightarrow{f_2} \dots \xrightarrow{f_{d-1}} X_{d} \xrightarrow{f_d} X_{d+1} \to 0 \end{align*}$$
$$\begin{align*}X_1 \xrightarrow{f_1} X_2 \xrightarrow{f_2} \dots \xrightarrow{f_{d-1}} X_{d} \xrightarrow{f_d} X_{d+1} \to 0 \end{align*}$$
 $f_0 \colon X_0 \to X_1$
in
$f_0 \colon X_0 \to X_1$
in
 $\mathcal {M}$
is called minimal if
$\mathcal {M}$
is called minimal if
 $f_i \in \operatorname {Rad}_{\mathcal {A}}(X_i,X_{i+1})$
for
$f_i \in \operatorname {Rad}_{\mathcal {A}}(X_i,X_{i+1})$
for
 $i=2,\ldots , d$
.
$i=2,\ldots , d$
.
-
(2) A d-kernel
of a morphism $$\begin{align*}0 \to X_0 \xrightarrow{f_0} X_1 \xrightarrow{f_1} \dots \xrightarrow{f_{d-2}} X_{d-1} \xrightarrow{f_{d-1}} X_{d} \end{align*}$$
$$\begin{align*}0 \to X_0 \xrightarrow{f_0} X_1 \xrightarrow{f_1} \dots \xrightarrow{f_{d-2}} X_{d-1} \xrightarrow{f_{d-1}} X_{d} \end{align*}$$
 $f_d \colon X_d \to X_{d+1}$
in
$f_d \colon X_d \to X_{d+1}$
in
 $\mathcal {M}$
is called minimal if
$\mathcal {M}$
is called minimal if
 $f_i \in \operatorname {Rad}_{\mathcal {A}}(X_i,X_{i+1})$
for
$f_i \in \operatorname {Rad}_{\mathcal {A}}(X_i,X_{i+1})$
for
 $i=0,\ldots , d-2$
.
$i=0,\ldots , d-2$
.
-
(3) A d-extension
in $$\begin{align*}0 \to X_0 \xrightarrow{f_0} X_1 \xrightarrow{f_1} \dots \xrightarrow{f_{d-1}} X_{d} \xrightarrow{f_d} X_{d+1}\to 0 \end{align*}$$
$$\begin{align*}0 \to X_0 \xrightarrow{f_0} X_1 \xrightarrow{f_1} \dots \xrightarrow{f_{d-1}} X_{d} \xrightarrow{f_d} X_{d+1}\to 0 \end{align*}$$
 $\mathcal {M}$
is called minimal if
$\mathcal {M}$
is called minimal if
 $f_i \in \operatorname {Rad}_{\mathcal {A}}(X_i,X_{i+1})$
for
$f_i \in \operatorname {Rad}_{\mathcal {A}}(X_i,X_{i+1})$
for
 $i=1,\ldots , d-1$
.
$i=1,\ldots , d-1$
.
Proposition 2.6 justifies the terminology in the definition above and shows that minimal d-cokernels, d-kernels and d-extensions exist and are unique up to isomorphism. When we say that a complex in a category
![]() $\mathcal {M}$
is a direct summand of another complex, this means that it is a direct summand in the category of complexes over
$\mathcal {M}$
is a direct summand of another complex, this means that it is a direct summand in the category of complexes over
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
Proposition 2.6 [Reference Herschend and JørgensenHJ, Proposition 2.4].
Let
![]() $\mathcal {M}$
be a d-cluster tilting subcategory of
$\mathcal {M}$
be a d-cluster tilting subcategory of
![]() $\mathcal {A}$
.
$\mathcal {A}$
.
-
(1) Given a morphism f in
 $\mathcal {M}$
, there exists a minimal d-cokernel (resp. d-kernel) of f. This d-cokernel (resp. d-kernel) is a direct summand of any other d-cokernel (resp. d-kernel) of f.
$\mathcal {M}$
, there exists a minimal d-cokernel (resp. d-kernel) of f. This d-cokernel (resp. d-kernel) is a direct summand of any other d-cokernel (resp. d-kernel) of f. -
(2) Given a d-extension in
 $\mathcal {M}$
, there exists an equivalent minimal d-extension. This minimal d-extension is a direct summand of every d-extension in the associated equivalence class.
$\mathcal {M}$
, there exists an equivalent minimal d-extension. This minimal d-extension is a direct summand of every d-extension in the associated equivalence class.
Remark 2.7 Since [Reference JassoJ2, Lemma 2.1] implies that any two d-cokernels of a morphism are isomorphic in the homotopy category, Proposition 2.6 implies that any d-cokernel is isomorphic to the direct sum of the minimal d-cokernel and a contractible exact sequence. Moreover, for an idempotent complete category (e.g., an abelian category), any contractible complex is the direct sum of complexes of the form
![]() $N \xrightarrow {1_N} N$
. In particular, given a d-cokernel
$N \xrightarrow {1_N} N$
. In particular, given a d-cokernel
of
![]() $f_0\colon X_0 \rightarrow X_1$
where
$f_0\colon X_0 \rightarrow X_1$
where
![]() $f_i \notin \operatorname {Rad}_{\mathcal {A}}(X_i, X_{i+1})$
for some
$f_i \notin \operatorname {Rad}_{\mathcal {A}}(X_i, X_{i+1})$
for some
![]() $2 \leq i\leq d$
, there is an isomorphic d-cokernel where
$2 \leq i\leq d$
, there is an isomorphic d-cokernel where
![]() $f_i$
is replaced by
$f_i$
is replaced by
 $$ \begin{align*} \begin{pmatrix} f_i' & 0 \\ 0 & 1_N \end{pmatrix}\colon X_{i}' \oplus N \rightarrow X_{i+1}' \oplus N \end{align*} $$
$$ \begin{align*} \begin{pmatrix} f_i' & 0 \\ 0 & 1_N \end{pmatrix}\colon X_{i}' \oplus N \rightarrow X_{i+1}' \oplus N \end{align*} $$
with
![]() $f_i' \in \operatorname {Rad}_{\mathcal {A}}(X_i', X_{i+1}')$
. Similar statements hold for d-kernels and d-extensions.
$f_i' \in \operatorname {Rad}_{\mathcal {A}}(X_i', X_{i+1}')$
. Similar statements hold for d-kernels and d-extensions.
The terminology in Definition 2.5 is further justified by the following connection to minimal morphisms.
Lemma 2.8 Let
![]() $X \xrightarrow {f} Y \xrightarrow {g} Z$
be a complex in
$X \xrightarrow {f} Y \xrightarrow {g} Z$
be a complex in
![]() $\mathcal {A}$
for which the induced sequence
$\mathcal {A}$
for which the induced sequence
is exact. The morphism f is left minimal if and only if
![]() $g\in \operatorname {Rad}_{\mathcal {A}}(Y,Z)$
.
$g\in \operatorname {Rad}_{\mathcal {A}}(Y,Z)$
.
Proof. See [Reference Jasso and KvammeJK, Lemma 1.1].
The construction of a minimal d-cokernel is frequently used throughout the paper. We discuss it in more detail in the following.
Construction 2.9. The minimal d-cokernel of a morphism
![]() $f \colon X \rightarrow Y$
in a d-cluster tilting subcategory
$f \colon X \rightarrow Y$
in a d-cluster tilting subcategory
![]() $\mathcal {M} \subseteq \mathcal {A}$
can be constructed as follows:
$\mathcal {M} \subseteq \mathcal {A}$
can be constructed as follows:
-
(1) Set
 $C_1=\operatorname {Coker} f$
and let
$C_1=\operatorname {Coker} f$
and let
 $g_1 \colon C_1 \to M_1$
be the minimal left
$g_1 \colon C_1 \to M_1$
be the minimal left
 $\mathcal {M}$
-approximation of
$\mathcal {M}$
-approximation of
 $C_1$
. Set
$C_1$
. Set
 ${f_1 \colon Y \to M_1}$
to be the composition
${f_1 \colon Y \to M_1}$
to be the composition
 $Y \rightarrow C_1 \xrightarrow {g_1} M_1$
.
$Y \rightarrow C_1 \xrightarrow {g_1} M_1$
. -
(2) Repeat on
 $f_1 \colon Y \to M_1$
to construct
$f_1 \colon Y \to M_1$
to construct
 $f_2 \colon M_1 \to M_2$
.
$f_2 \colon M_1 \to M_2$
. -
(3) Iterate the procedure, which must terminate and result in a d-cokernel by [Reference JassoJ2, Proposition 3.17].
Since each morphism
![]() $f_i$
is the composition of an epimorphism and a left minimal morphism, they are all left minimal, and hence, Lemma 2.8 shows that this is the minimal d-cokernel of f. Note that each
$f_i$
is the composition of an epimorphism and a left minimal morphism, they are all left minimal, and hence, Lemma 2.8 shows that this is the minimal d-cokernel of f. Note that each
![]() $f_i$
can equivalently be described as the left minimal weak cokernel of the previous morphism.
$f_i$
can equivalently be described as the left minimal weak cokernel of the previous morphism.
Lemma 2.10. Suppose we have a d-extension
Then, for any morphism
![]() $h \colon X \to F_0$
, there is a d-pushout diagram
$h \colon X \to F_0$
, there is a d-pushout diagram

such that the bottom row is a minimal d-extension.
Proof. The fact that a d-pushout diagram exists is precisely [Reference JassoJ2, Theorem 3.8]. It follows from [Reference JassoJ2, Proposition 4.8] that the bottom row is a d-extension with last term equal to Y. If this d-extension is minimal, then we are done. Otherwise, it has a minimal d-extension as a direct summand by Proposition 2.6. Composing the morphism in the statement with the projection onto this minimal d-extension gives another commutative diagram, which is a d-pushout by [Reference JassoJ2, Proposition 4.8]. The bottom row of this new diagram is a minimal d-extension as required.
Note that there is a dual version of Lemma 2.10 which will also be used.
2.3 Torsion and d-torsion classes
Generalising the properties of the class of torsion groups in the category of abelian groups, the notion of a torsion pair was introduced in [Reference DicksonD] as follows.
Definition 2.11. A pair
![]() $(\mathcal {T}, \mathcal {F})$
of subcategories of
$(\mathcal {T}, \mathcal {F})$
of subcategories of
![]() $\mathcal {A}$
is a torsion pair if the following conditions are satisfied:
$\mathcal {A}$
is a torsion pair if the following conditions are satisfied:
-
(1) For every
 $X \in \mathcal {A}$
, there exists a short exact sequence where
$X \in \mathcal {A}$
, there exists a short exact sequence where $$\begin{align*}0\to tX \rightarrow X \rightarrow fX \to 0,\end{align*}$$
$$\begin{align*}0\to tX \rightarrow X \rightarrow fX \to 0,\end{align*}$$
 $tX\in \mathcal {T}$
and
$tX\in \mathcal {T}$
and
 $fX\in \mathcal {F}$
.
$fX\in \mathcal {F}$
.
-
(2)
 $\operatorname {Hom}_{\mathcal {A}} (X,Y)=0$
for all
$\operatorname {Hom}_{\mathcal {A}} (X,Y)=0$
for all
 $X \in \mathcal {T}$
and
$X \in \mathcal {T}$
and
 $Y \in \mathcal {F}$
.
$Y \in \mathcal {F}$
.
Given a torsion pair
![]() $(\mathcal {T}, \mathcal {F})$
, we say that
$(\mathcal {T}, \mathcal {F})$
, we say that
![]() $\mathcal {T}$
is a torsion class and
$\mathcal {T}$
is a torsion class and
![]() $\mathcal {F}$
a torsion-free class.
$\mathcal {F}$
a torsion-free class.
Note that the short exact sequence from the definition above is unique up to isomorphism. The following classical result characterises torsion classes in
![]() $\mathcal {A}$
as those subcategories which are closed under extensions and quotients.
$\mathcal {A}$
as those subcategories which are closed under extensions and quotients.
Theorem 2.12 [Reference DicksonD, Theorem 2.3].
A subcategory
![]() $\mathcal {T}$
of
$\mathcal {T}$
of
![]() $\mathcal {A}$
is a torsion class if and only if
$\mathcal {A}$
is a torsion class if and only if
![]() $\mathcal {T}$
is closed under extensions and quotients.
$\mathcal {T}$
is closed under extensions and quotients.
We denote by
![]() $\text {tors}(\mathcal {A})$
the poset of all torsion classes in
$\text {tors}(\mathcal {A})$
the poset of all torsion classes in
![]() $\mathcal {A}$
ordered by inclusion. It is well known that
$\mathcal {A}$
ordered by inclusion. It is well known that
![]() $\text {tors}(\mathcal {A})$
is a complete lattice where the meet is given by intersection; see, for example, [Reference Iyama, Reiten, Thomas and TodorovIRTT, Proposition 2.3].
$\text {tors}(\mathcal {A})$
is a complete lattice where the meet is given by intersection; see, for example, [Reference Iyama, Reiten, Thomas and TodorovIRTT, Proposition 2.3].
In light of the development of higher homological algebra, it is natural to consider higher analogues of torsion classes. The notion of d-torsion classes was introduced in [Reference JørgensenJø].
Definition 2.13 [Reference JørgensenJø, Definition 1.1].
Let
![]() $\mathcal {M}$
be a d-abelian category. A subcategory
$\mathcal {M}$
be a d-abelian category. A subcategory
![]() $\mathcal {U}$
of
$\mathcal {U}$
of
![]() $\mathcal {M}$
is a d-torsion class if for every M in
$\mathcal {M}$
is a d-torsion class if for every M in
![]() $\mathcal {M}$
, there exists a d-exact sequence
$\mathcal {M}$
, there exists a d-exact sequence
such that the following conditions are satisfied:
-
(1) The object
 $U_M$
is in
$U_M$
is in
 $\mathcal {U}$
.
$\mathcal {U}$
. -
(2) The sequence
 $0 \rightarrow \operatorname {Hom}_{\mathcal {M}}(U,V_1) \rightarrow \cdots \rightarrow \operatorname {Hom}_{\mathcal {M}}(U,V_d) \rightarrow 0$
is exact for every U in
$0 \rightarrow \operatorname {Hom}_{\mathcal {M}}(U,V_1) \rightarrow \cdots \rightarrow \operatorname {Hom}_{\mathcal {M}}(U,V_d) \rightarrow 0$
is exact for every U in
 $\mathcal {U}$
.
$\mathcal {U}$
.
The object
![]() $U_M$
above is known as the d-torsion subobject of M with respect to
$U_M$
above is known as the d-torsion subobject of M with respect to
![]() $\mathcal {U}$
.
$\mathcal {U}$
.
Note that when
![]() $d=1$
, the previous definition is equivalent to the definition of a torsion class; c.f. Definition 2.11.
$d=1$
, the previous definition is equivalent to the definition of a torsion class; c.f. Definition 2.11.
Remark 2.14. Our standing assumption that subcategories are closed under finite direct sums and summands is not necessary in Definition 2.13, as this follows from [Reference JørgensenJø, Lemma 2.7(iii)].
A recent paper [Reference Asadollahi, Jørgensen, Schroll and TreffingerAJST] showed that there is a strong relationship between the torsion classes in an abelian category
![]() $\mathcal {A}$
and the d-torsion classes in a d-cluster tilting subcategory
$\mathcal {A}$
and the d-torsion classes in a d-cluster tilting subcategory
![]() $\mathcal {M}$
of
$\mathcal {M}$
of
![]() $\mathcal {A}$
.
$\mathcal {A}$
.
Theorem 2.15 [Reference Asadollahi, Jørgensen, Schroll and TreffingerAJST, Theorem 1.1].
Let
![]() $\mathcal {M}$
be a d-cluster tilting subcategory of
$\mathcal {M}$
be a d-cluster tilting subcategory of
![]() $\mathcal {A}$
. Then a torsion class
$\mathcal {A}$
. Then a torsion class
![]() $\mathcal {T}$
in
$\mathcal {T}$
in
![]() $\mathcal {A}$
is the minimal torsion class containing a given d-torsion class in
$\mathcal {A}$
is the minimal torsion class containing a given d-torsion class in
![]() $\mathcal {M}$
if and only if the following conditions are satisfied:
$\mathcal {M}$
if and only if the following conditions are satisfied:
-
(1) For every
 $M\in \mathcal {M}$
, we have
$M\in \mathcal {M}$
, we have
 $tM\in \mathcal {M}$
.
$tM\in \mathcal {M}$
. -
(2)
 $\mathcal {T}$
is the smallest torsion class containing all
$\mathcal {T}$
is the smallest torsion class containing all
 $tM$
for
$tM$
for
 $M\in \mathcal {M}$
.
$M\in \mathcal {M}$
. -
(3) For any
 $M,M'\in \mathcal {M}$
, we have
$M,M'\in \mathcal {M}$
, we have
 $\operatorname {Ext}^{d-1}_{\mathcal {A}}(tM,fM')=0$
.
$\operatorname {Ext}^{d-1}_{\mathcal {A}}(tM,fM')=0$
.
Moreover, in this case, ![]() is a d-torsion class and
is a d-torsion class and
![]() $\mathcal {T}$
is the minimal torsion class containing it. Furthermore, we have
$\mathcal {T}$
is the minimal torsion class containing it. Furthermore, we have
![]() $U_M \cong tM$
for every object
$U_M \cong tM$
for every object
![]() $M \in \mathcal {M}$
.
$M \in \mathcal {M}$
.
We now illustrate Theorem 2.15 in our running example.
Example 2.16. Let A and
![]() $\mathcal {M}$
be as in Example 2.4. In Table 1, we give the complete list of
$\mathcal {M}$
be as in Example 2.4. In Table 1, we give the complete list of
![]() $2$
-torsion classes
$2$
-torsion classes
![]() $\mathcal {U}$
in
$\mathcal {U}$
in
![]() $\mathcal {M}$
and the corresponding minimal torsion classes
$\mathcal {M}$
and the corresponding minimal torsion classes
![]() $\mathcal {T}$
in
$\mathcal {T}$
in
![]() $\operatorname {mod}A$
such that
$\operatorname {mod}A$
such that
![]() $\mathcal {U}=\mathcal {T} \cap \mathcal {M}$
.
$\mathcal {U}=\mathcal {T} \cap \mathcal {M}$
.
Table 1 The
![]() $2$
-torsion classes considered in Example 2.16 and their corresponding torsion classes.
$2$
-torsion classes considered in Example 2.16 and their corresponding torsion classes.

On one hand, we note that although Theorem 2.15 gives a complete characterisation of the minimal torsion classes
![]() $\mathcal {T}$
in
$\mathcal {T}$
in
![]() $\operatorname {mod}A$
such that
$\operatorname {mod}A$
such that
![]() $\mathcal {T}\cap \mathcal {M}$
is a
$\mathcal {T}\cap \mathcal {M}$
is a
![]() $2$
-torsion class in
$2$
-torsion class in
![]() $\mathcal {M}$
, there are other torsion classes in
$\mathcal {M}$
, there are other torsion classes in
![]() $\operatorname {mod}A$
with this property. For instance, we see that
$\operatorname {mod}A$
with this property. For instance, we see that
![]() $\mathcal {T}=\operatorname {add}\left \{{\tiny \begin {matrix} 2 \end {matrix}}\oplus {\tiny \begin {matrix} 1\\2 \end {matrix}}\oplus {\tiny \begin {matrix} 1 \end {matrix}} \right \}$
is a torsion class in
$\mathcal {T}=\operatorname {add}\left \{{\tiny \begin {matrix} 2 \end {matrix}}\oplus {\tiny \begin {matrix} 1\\2 \end {matrix}}\oplus {\tiny \begin {matrix} 1 \end {matrix}} \right \}$
is a torsion class in
![]() $\operatorname {mod}A$
and
$\operatorname {mod}A$
and
![]() $\mathcal {T}\cap \mathcal {M} = \operatorname {add}\left \{{\tiny \begin {matrix} 1\\2 \end {matrix}}\oplus {\tiny \begin {matrix} 1 \end {matrix}} \right \}$
is a
$\mathcal {T}\cap \mathcal {M} = \operatorname {add}\left \{{\tiny \begin {matrix} 1\\2 \end {matrix}}\oplus {\tiny \begin {matrix} 1 \end {matrix}} \right \}$
is a
![]() $2$
-torsion class in
$2$
-torsion class in
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
On the other hand, it is not true that
![]() $\mathcal {T}\cap \mathcal {M}$
is a
$\mathcal {T}\cap \mathcal {M}$
is a
![]() $2$
-torsion class in
$2$
-torsion class in
![]() $\mathcal {M}$
for every torsion class
$\mathcal {M}$
for every torsion class
![]() $\mathcal {T}$
in
$\mathcal {T}$
in
![]() $\operatorname {mod}A$
. Two such examples are
$\operatorname {mod}A$
. Two such examples are
![]() $\mathcal {T}_1=\operatorname {add}\left \{{\tiny \begin {matrix} 3 \end {matrix}}\oplus {\tiny \begin {matrix} 1 \end {matrix}} \right \}$
and
$\mathcal {T}_1=\operatorname {add}\left \{{\tiny \begin {matrix} 3 \end {matrix}}\oplus {\tiny \begin {matrix} 1 \end {matrix}} \right \}$
and
![]() $\mathcal {T}_2 = \operatorname {add}\left \{{\tiny \begin {matrix} 3 \end {matrix}}\oplus {\tiny \begin {matrix} 2\\3 \end {matrix}}\oplus {\tiny \begin {matrix} 2 \end {matrix}} \right \}$
. The intersections
$\mathcal {T}_2 = \operatorname {add}\left \{{\tiny \begin {matrix} 3 \end {matrix}}\oplus {\tiny \begin {matrix} 2\\3 \end {matrix}}\oplus {\tiny \begin {matrix} 2 \end {matrix}} \right \}$
. The intersections
![]() $\mathcal {T}_1\cap \mathcal {M}$
and
$\mathcal {T}_1\cap \mathcal {M}$
and
![]() $\mathcal {T}_2\cap \mathcal {M}$
are not
$\mathcal {T}_2\cap \mathcal {M}$
are not
![]() $2$
-torsion classes in
$2$
-torsion classes in
![]() $\mathcal {M}$
, for reasons that will be explained in Example 3.18.
$\mathcal {M}$
, for reasons that will be explained in Example 3.18.
3 Closure under d-extensions and d-quotients
Throughout this section, let
![]() $\mathcal {M}$
be a d-cluster tilting subcategory of the abelian category
$\mathcal {M}$
be a d-cluster tilting subcategory of the abelian category
![]() $\mathcal {A}$
. We also introduce the following setup, which will not be assumed unless explicitly stated.
$\mathcal {A}$
. We also introduce the following setup, which will not be assumed unless explicitly stated.
Setup 3.1. Let
![]() $\mathcal {U}$
be a d-torsion class in
$\mathcal {U}$
be a d-torsion class in
![]() $\mathcal {M}$
. Let
$\mathcal {M}$
. Let
![]() $\mathcal {T}$
be a torsion class in
$\mathcal {T}$
be a torsion class in
![]() $\mathcal {A}$
such that
$\mathcal {A}$
such that
![]() $\mathcal {U} = \mathcal {T} \cap \mathcal {M}$
and the torsion subobject
$\mathcal {U} = \mathcal {T} \cap \mathcal {M}$
and the torsion subobject
![]() $tM$
of M belongs to
$tM$
of M belongs to
![]() $\mathcal {M}$
for all
$\mathcal {M}$
for all
![]() $M \in \mathcal {M}$
.
$M \in \mathcal {M}$
.
We note that Theorem 2.15 implies that for every d-torsion class
![]() $\mathcal {U}$
in
$\mathcal {U}$
in
![]() $\mathcal {M}$
, we can find a torsion class
$\mathcal {M}$
, we can find a torsion class
![]() $\mathcal {T}$
satisfying Setup 3.1.
$\mathcal {T}$
satisfying Setup 3.1.
Section 3 is divided into three subsections. We first verify some consequences of the setup above in Section 3.1. In Section 3.2, we state and prove the main result of this paper – namely, the characterisation of higher torsion classes given in Theorem 1.1. The aim of Section 3.3 is to prove Theorem 1.3.
3.1 Approximations by d-torsion classes
Throughout this subsection, we assume Setup 3.1.
Lemma 3.2. For any
![]() $M \in \mathcal {M}$
, there is an isomorphism
$M \in \mathcal {M}$
, there is an isomorphism
![]() $U_M \cong tM$
commuting with the inclusion to M.
$U_M \cong tM$
commuting with the inclusion to M.
Proof. By the definition of a d-torsion class, the morphism
![]() $U_M\to M$
is a right
$U_M\to M$
is a right
![]() $\mathcal {U}$
-approximation. Since the morphism
$\mathcal {U}$
-approximation. Since the morphism
![]() $tM\to M$
is a right
$tM\to M$
is a right
![]() $\mathcal {T}$
-approximation and
$\mathcal {T}$
-approximation and
![]() $tM\in \mathcal {U}$
, it must also be a right
$tM\in \mathcal {U}$
, it must also be a right
![]() $\mathcal {U}$
-approximation. Hence, the inclusions
$\mathcal {U}$
-approximation. Hence, the inclusions
![]() $U_M\to M$
and
$U_M\to M$
and
![]() $tM\to M$
must factor through each other, which implies that
$tM\to M$
must factor through each other, which implies that
![]() $U_M\cong tM$
.
$U_M\cong tM$
.
By Lemma 3.2, we can assume
![]() $U_M=tM$
whenever we are in Setup 3.1, and we will do this from now on. Given Setup 3.1, we gain additional control of left
$U_M=tM$
whenever we are in Setup 3.1, and we will do this from now on. Given Setup 3.1, we gain additional control of left
![]() $\mathcal {M}$
-approximations of objects in
$\mathcal {M}$
-approximations of objects in
![]() $\mathcal {T}$
.
$\mathcal {T}$
.
Lemma 3.3. Let
![]() $\phi _X\colon X \rightarrow M$
be the minimal left
$\phi _X\colon X \rightarrow M$
be the minimal left
![]() $\mathcal {M}$
-approximation of an object X in
$\mathcal {M}$
-approximation of an object X in
![]() $\mathcal {T}$
. Then M is in
$\mathcal {T}$
. Then M is in
![]() $\mathcal {U}$
.
$\mathcal {U}$
.
Proof. Consider the short exact sequence
associated to the torsion pair
![]() $(\mathcal {T},\mathcal {F})$
. The morphism
$(\mathcal {T},\mathcal {F})$
. The morphism
![]() $\iota $
is a right
$\iota $
is a right
![]() $\mathcal {T}$
-approximation of M, and
$\mathcal {T}$
-approximation of M, and
![]() $tM \in \mathcal {M}$
by assumption. As
$tM \in \mathcal {M}$
by assumption. As
![]() $X \in \mathcal {T}$
, there exists a morphism
$X \in \mathcal {T}$
, there exists a morphism
![]() $\psi _X \colon X \to tM$
such that
$\psi _X \colon X \to tM$
such that
![]() $\iota \psi _X = \phi _X$
. Notice that since
$\iota \psi _X = \phi _X$
. Notice that since
![]() $\phi _X$
is a left
$\phi _X$
is a left
![]() $\mathcal {M}$
-approximation of X, so is
$\mathcal {M}$
-approximation of X, so is
![]() $\psi _X$
. Since
$\psi _X$
. Since
![]() $\phi _X$
is left minimal and
$\phi _X$
is left minimal and
![]() $\iota $
is a monomorphism, this implies that M is isomorphic to
$\iota $
is a monomorphism, this implies that M is isomorphic to
![]() $tM$
. Consequently, one obtains that M is contained in
$tM$
. Consequently, one obtains that M is contained in
![]() $\mathcal {T}$
, and hence also in
$\mathcal {T}$
, and hence also in
![]() $\mathcal {U}$
.
$\mathcal {U}$
.
Corollary 3.4. If
![]() $X \in \mathcal {T}$
, then the minimal left
$X \in \mathcal {T}$
, then the minimal left
![]() $\mathcal {M}$
-approximation of X is also the minimal left
$\mathcal {M}$
-approximation of X is also the minimal left
![]() $\mathcal {U}$
-approximation of X. Moreover, this approximation is a monomorphism.
$\mathcal {U}$
-approximation of X. Moreover, this approximation is a monomorphism.
Proof. Let
![]() $\phi _X\colon X \rightarrow M$
be the minimal left
$\phi _X\colon X \rightarrow M$
be the minimal left
![]() $\mathcal {M}$
-approximation of X. By Lemma 3.3, we know that
$\mathcal {M}$
-approximation of X. By Lemma 3.3, we know that
![]() $M \in \mathcal {U}$
, and it follows that
$M \in \mathcal {U}$
, and it follows that
![]() $\phi _X$
is also a left
$\phi _X$
is also a left
![]() $\mathcal {U}$
-approximation. Since
$\mathcal {U}$
-approximation. Since
![]() $\phi _X$
is left minimal, it is the minimal left
$\phi _X$
is left minimal, it is the minimal left
![]() $\mathcal {U}$
-approximation of X. Finally, since
$\mathcal {U}$
-approximation of X. Finally, since
![]() $\mathcal {M}$
is cogenerating, any left
$\mathcal {M}$
is cogenerating, any left
![]() $\mathcal {M}$
-approximation is a monomorphism.
$\mathcal {M}$
-approximation is a monomorphism.
Remark 3.5. Note that the previous corollary implies that the d-torsion class
![]() $\mathcal {U}$
is always covariantly finite within the torsion class
$\mathcal {U}$
is always covariantly finite within the torsion class
![]() $\mathcal {T}$
, even if
$\mathcal {T}$
, even if
![]() $\mathcal {U}$
is not covariantly finite in
$\mathcal {U}$
is not covariantly finite in
![]() $\mathcal {M}$
or
$\mathcal {M}$
or
![]() $\mathcal {A}$
.
$\mathcal {A}$
.
3.2 Characterising d-torsion classes
In order to formulate our results, we need higher analogues of what it means for a subcategory to be closed under extensions and quotients. Recall the notions of d-cokernels and d-extensions from Section 2.1.
The following definition already appeared in the literature; see, for example, [Reference Herschend, Jørgensen and VasoHJV, Definition 2.8(iii)] or [Reference Herschend, Liu and NakaokaHLN2, Definition 4.1].
Definition 3.6. A subcategory
![]() $\mathcal {U}$
of
$\mathcal {U}$
of
![]() $\mathcal {M}$
is called closed under d-extensions if for any d-extension
$\mathcal {M}$
is called closed under d-extensions if for any d-extension
in
![]() $\mathcal {M}$
with X and Y in
$\mathcal {M}$
with X and Y in
![]() $\mathcal {U}$
, there exists an equivalent d-extension
$\mathcal {U}$
, there exists an equivalent d-extension
where all the objects are in
![]() $\mathcal {U}$
.
$\mathcal {U}$
.
Definition 3.7. A subcategory
![]() $\mathcal {U}$
of
$\mathcal {U}$
of
![]() $\mathcal {M}$
is called closed under d-quotients if for any morphism
$\mathcal {M}$
is called closed under d-quotients if for any morphism
![]() $f \colon M \rightarrow U$
in
$f \colon M \rightarrow U$
in
![]() $\mathcal {M}$
with U in
$\mathcal {M}$
with U in
![]() $\mathcal {U}$
, there exists a d-cokernel
$\mathcal {U}$
, there exists a d-cokernel
of f with
![]() $E_i$
in
$E_i$
in
![]() $\mathcal {U}$
for all
$\mathcal {U}$
for all
![]() $i = 1,\ldots , d$
. If this condition is only assumed to hold when both M and U belong to
$i = 1,\ldots , d$
. If this condition is only assumed to hold when both M and U belong to
![]() $\mathcal {U}$
, we say that
$\mathcal {U}$
, we say that
![]() $\mathcal {U}$
is closed under d-cokernels.
$\mathcal {U}$
is closed under d-cokernels.
It will further be convenient to define a (minimal) d-quotient of
![]() $U \in \mathcal {M}$
as a (minimal) d-cokernel of some morphism
$U \in \mathcal {M}$
as a (minimal) d-cokernel of some morphism
![]() $f \colon M \to U$
in
$f \colon M \to U$
in
![]() $\mathcal {M}$
. The following lemma shows that closure under d-quotients or d-extensions is equivalent to closure under minimal d-quotients or d-extensions. This uses the standing assumption that our subcategories are closed under direct summands.
$\mathcal {M}$
. The following lemma shows that closure under d-quotients or d-extensions is equivalent to closure under minimal d-quotients or d-extensions. This uses the standing assumption that our subcategories are closed under direct summands.
Lemma 3.8. Let
![]() $\mathcal {U}$
be a subcategory of
$\mathcal {U}$
be a subcategory of
![]() $\mathcal {M}$
. The following hold:
$\mathcal {M}$
. The following hold:
-
(1)
 $\mathcal {U}$
is closed under d-extensions if and only if for any minimal d-extension with
$\mathcal {U}$
is closed under d-extensions if and only if for any minimal d-extension with $$\begin{align*}0 \to X \to E_1 \to \cdots \to E_d \to Y \to 0 \end{align*}$$
$$\begin{align*}0 \to X \to E_1 \to \cdots \to E_d \to Y \to 0 \end{align*}$$
 $X, Y \in \mathcal {U}$
, we have
$X, Y \in \mathcal {U}$
, we have
 $E_1, \dots , E_d \in \mathcal {U}$
.
$E_1, \dots , E_d \in \mathcal {U}$
.
-
(2)
 $\mathcal {U}$
is closed under d-quotients if and only if for any minimal d-cokernel of a morphism
$\mathcal {U}$
is closed under d-quotients if and only if for any minimal d-cokernel of a morphism $$\begin{align*}M \xrightarrow{} U \rightarrow E_1 \rightarrow E_2 \rightarrow \dots \rightarrow E_{d} \to 0 \end{align*}$$
$$\begin{align*}M \xrightarrow{} U \rightarrow E_1 \rightarrow E_2 \rightarrow \dots \rightarrow E_{d} \to 0 \end{align*}$$
 $M \to U$
in
$M \to U$
in
 $\mathcal {M}$
with
$\mathcal {M}$
with
 $U \in \mathcal {U}$
, we have
$U \in \mathcal {U}$
, we have
 $E_1, \dots , E_d \in \mathcal {U}$
.
$E_1, \dots , E_d \in \mathcal {U}$
.
Proof. By Proposition 2.6, any equivalence class of d-extensions contains a unique (up to isomorphism) minimal d-extension, which is furthermore a direct summand of any other d-extension in the class. This immediately implies (1), since
![]() $\mathcal {U}$
is closed under direct summands. Part (2) is proved similarly, using that the minimal d-cokernel of a morphism f is a summand of any other d-cokernel of f.
$\mathcal {U}$
is closed under direct summands. Part (2) is proved similarly, using that the minimal d-cokernel of a morphism f is a summand of any other d-cokernel of f.
Remark 3.9. For a direct sum
![]() $X \oplus Y \in \mathcal {M}$
, we have
$X \oplus Y \in \mathcal {M}$
, we have
![]() $X,Y\in \mathcal {M}$
and the projection
$X,Y\in \mathcal {M}$
and the projection
![]() $X \oplus Y \to Y$
gives a minimal d-cokernel
$X \oplus Y \to Y$
gives a minimal d-cokernel
of the inclusion
![]() $X \to X \oplus Y$
.
$X \to X \oplus Y$
.
Hence, being closed under minimal d-quotients implies being closed under direct summands.
Remark 2.14 and Remark 3.9 show that the standing assumption on subcategories being closed under direct summands is not a significant restriction.
The following lemma shows that when checking if a subcategory is closed under d-extensions, it is often sufficient to consider the first middle term. This simplifies the proof of Proposition 3.11 and is also an important step towards the main result in Section 3.3.
Lemma 3.10. Let
![]() $\mathcal {U} \subseteq \mathcal {M}$
be closed under d-quotients. Then for any minimal d-extension
$\mathcal {U} \subseteq \mathcal {M}$
be closed under d-quotients. Then for any minimal d-extension
in
![]() $\mathcal {M}$
with
$\mathcal {M}$
with
![]() $X,E_1,Y \in \mathcal {U}$
, it follows that
$X,E_1,Y \in \mathcal {U}$
, it follows that
![]() $E_i \in \mathcal {U}$
for
$E_i \in \mathcal {U}$
for
![]() $i=2, \dots , d$
.
$i=2, \dots , d$
.
Proof. The minimality of the d-extension (see Definition 2.5) gives that
![]() $e_i \in \operatorname {Rad}_{\mathcal {A}}(E_i, E_{i+1})$
for all
$e_i \in \operatorname {Rad}_{\mathcal {A}}(E_i, E_{i+1})$
for all
![]() $i=1, \dots , d-1$
. Moreover, the sequence
$i=1, \dots , d-1$
. Moreover, the sequence
is a d-cokernel of f. If
![]() $g \in \operatorname {Rad}_{\mathcal {A}}(E_d,Y)$
, then this d-cokernel is minimal. Since
$g \in \operatorname {Rad}_{\mathcal {A}}(E_d,Y)$
, then this d-cokernel is minimal. Since
![]() $E_1 \in \mathcal {U}$
, the result then follows from
$E_1 \in \mathcal {U}$
, the result then follows from
![]() $\mathcal {U}$
being closed under minimal d-quotients by Lemma 3.8.
$\mathcal {U}$
being closed under minimal d-quotients by Lemma 3.8.
Suppose hence that
![]() $g \notin \operatorname {Rad}_{\mathcal {A}}(E_d,Y)$
. Recall from Remark 2.7 that the sequence (2) is isomorphic to the direct sum of the minimal d-cokernel of f and shifted complexes of the form
$g \notin \operatorname {Rad}_{\mathcal {A}}(E_d,Y)$
. Recall from Remark 2.7 that the sequence (2) is isomorphic to the direct sum of the minimal d-cokernel of f and shifted complexes of the form
![]() $N \xrightarrow {1_N} N$
. However, since
$N \xrightarrow {1_N} N$
. However, since
![]() $e_i \in \operatorname {Rad}_A(E_i,E_{i+1})$
for
$e_i \in \operatorname {Rad}_A(E_i,E_{i+1})$
for
![]() $i=1, \dots d-1$
, it follows that (2) is isomorphic to
$i=1, \dots d-1$
, it follows that (2) is isomorphic to
 $$ \begin{align*} E_1 \xrightarrow{e_1} E_2 \xrightarrow{e_2} \cdots \xrightarrow{e_{d-2}} E_{d-1} \xrightarrow{e_{d-1}'=\left(\begin{smallmatrix} h_1 \\ 0 \end{smallmatrix}\right)} E^{\prime}_d \oplus Y" \xrightarrow{\left(\begin{smallmatrix} g' & 0 \\ 0 & 1_{Y"} \end{smallmatrix}\right)} Y' \oplus Y" \to 0, \end{align*} $$
$$ \begin{align*} E_1 \xrightarrow{e_1} E_2 \xrightarrow{e_2} \cdots \xrightarrow{e_{d-2}} E_{d-1} \xrightarrow{e_{d-1}'=\left(\begin{smallmatrix} h_1 \\ 0 \end{smallmatrix}\right)} E^{\prime}_d \oplus Y" \xrightarrow{\left(\begin{smallmatrix} g' & 0 \\ 0 & 1_{Y"} \end{smallmatrix}\right)} Y' \oplus Y" \to 0, \end{align*} $$
where
![]() $e_{d-1}'$
is
$e_{d-1}'$
is
![]() $e_{d-1}$
composed with an isomorphism and
$e_{d-1}$
composed with an isomorphism and
is a minimal d-cokernel of f. In particular, the objects
![]() $E_2, \dots , E_{d-1},E_d'$
are in
$E_2, \dots , E_{d-1},E_d'$
are in
![]() $\mathcal {U}$
as
$\mathcal {U}$
as
![]() $E_1\in \mathcal {U}$
and
$E_1\in \mathcal {U}$
and
![]() $\mathcal {U}$
is closed under minimal d-quotients by Lemma 3.8. Since
$\mathcal {U}$
is closed under minimal d-quotients by Lemma 3.8. Since
![]() $Y'\oplus Y" = Y \in \mathcal {U}$
and
$Y'\oplus Y" = Y \in \mathcal {U}$
and
![]() $\mathcal {U}$
is closed under direct summands, we have that
$\mathcal {U}$
is closed under direct summands, we have that
![]() $Y"\in \mathcal {U}$
. Hence,
$Y"\in \mathcal {U}$
. Hence,
![]() $E_d=E_d' \oplus Y"\in \mathcal {U}$
, completing the proof.
$E_d=E_d' \oplus Y"\in \mathcal {U}$
, completing the proof.
We are now ready to prove the first part of our characterisation result.
Proposition 3.11. Let
![]() $\mathcal {U} \subseteq \mathcal {M}$
be a d-torsion class. Then
$\mathcal {U} \subseteq \mathcal {M}$
be a d-torsion class. Then
![]() $\mathcal {U}$
is closed under d-extensions and d-quotients.
$\mathcal {U}$
is closed under d-extensions and d-quotients.
Proof. As
![]() $\mathcal {U}$
is a d-torsion class in
$\mathcal {U}$
is a d-torsion class in
![]() $\mathcal {M}$
, we have that
$\mathcal {M}$
, we have that
![]() $\mathcal {U} = \mathcal {T} \cap \mathcal {M}$
for some torsion class
$\mathcal {U} = \mathcal {T} \cap \mathcal {M}$
for some torsion class
![]() $\mathcal {T}$
in
$\mathcal {T}$
in
![]() $\mathcal {A}$
as in Setup 3.1. Recall from Lemma 3.8 that it suffices to consider minimal d-extensions and minimal d-quotients.
$\mathcal {A}$
as in Setup 3.1. Recall from Lemma 3.8 that it suffices to consider minimal d-extensions and minimal d-quotients.
We first show that
![]() $\mathcal {U}$
is closed under minimal d-quotients. Let
$\mathcal {U}$
is closed under minimal d-quotients. Let
![]() $f \colon M \to U$
be a morphism in
$f \colon M \to U$
be a morphism in
![]() $\mathcal {M}$
with
$\mathcal {M}$
with
![]() $U \in \mathcal {U}$
and consider its minimal d-cokernel
$U \in \mathcal {U}$
and consider its minimal d-cokernel
By construction of the minimal d-cokernel (see Construction 2.9), we have that
![]() $V_i$
arises as the minimal left
$V_i$
arises as the minimal left
![]() $\mathcal {M}$
-approximation of
$\mathcal {M}$
-approximation of
![]() $\operatorname {Coker} f_{i-1}$
for all
$\operatorname {Coker} f_{i-1}$
for all
![]() $i= 1,\ldots , d$
, where we set
$i= 1,\ldots , d$
, where we set
![]() $f_0 = f$
. As
$f_0 = f$
. As
![]() $U \in \mathcal {U} = \mathcal {T} \cap \mathcal {M}$
and
$U \in \mathcal {U} = \mathcal {T} \cap \mathcal {M}$
and
![]() $\mathcal {T}$
is closed under quotients, Lemma 3.3 implies that
$\mathcal {T}$
is closed under quotients, Lemma 3.3 implies that
![]() $V_i \in \mathcal {U}$
for all
$V_i \in \mathcal {U}$
for all
![]() $i= 1,\ldots , d$
. This shows that
$i= 1,\ldots , d$
. This shows that
![]() $\mathcal {U}$
is closed under minimal d-quotients.
$\mathcal {U}$
is closed under minimal d-quotients.
We next prove that
![]() $\mathcal {U}$
is closed under minimal d-extensions. Consider a minimal d-exact sequence
$\mathcal {U}$
is closed under minimal d-extensions. Consider a minimal d-exact sequence
in
![]() $\mathcal {M}$
with X and Y in
$\mathcal {M}$
with X and Y in
![]() $\mathcal {U}$
. By Lemma 2.8, the morphism
$\mathcal {U}$
. By Lemma 2.8, the morphism
![]() $e_i$
is left minimal for
$e_i$
is left minimal for
![]() $i=0,\dots ,d-2$
. As
$i=0,\dots ,d-2$
. As
![]() $\mathcal {U}$
is a d-torsion class, we obtain the solid part of the diagram
$\mathcal {U}$
is a d-torsion class, we obtain the solid part of the diagram

where the bottom row is the d-exact sequence associated to
![]() $E_1$
by
$E_1$
by
![]() $\mathcal {U}$
. In particular, the object
$\mathcal {U}$
. In particular, the object
![]() $tE_1 \in \mathcal {U}$
is the d-torsion subobject of
$tE_1 \in \mathcal {U}$
is the d-torsion subobject of
![]() $E_1$
with respect to
$E_1$
with respect to
![]() $\mathcal {U}$
by Lemma 3.2, and the sequence
$\mathcal {U}$
by Lemma 3.2, and the sequence
is exact for every U in
![]() $\mathcal {U}$
. As
$\mathcal {U}$
. As
![]() $\iota $
is a right
$\iota $
is a right
![]() $\mathcal {T}$
-approximation and
$\mathcal {T}$
-approximation and
![]() $X \in \mathcal {U} = \mathcal {T} \cap \mathcal {M}$
, there exists a morphism
$X \in \mathcal {U} = \mathcal {T} \cap \mathcal {M}$
, there exists a morphism
![]() $g_0 \colon X \to tE_1$
making the left square commute. We can hence complete the diagram to a morphism g of d-exact sequences by using the factorisation property for weak cokernels; see Section 2.1.
$g_0 \colon X \to tE_1$
making the left square commute. We can hence complete the diagram to a morphism g of d-exact sequences by using the factorisation property for weak cokernels; see Section 2.1.
Since (3) is exact and
![]() $Y\in \mathcal {U}$
, the morphism
$Y\in \mathcal {U}$
, the morphism
is surjective. Hence, there exists a morphism
![]() $h_d\colon Y \to W_{d-1}$
with
$h_d\colon Y \to W_{d-1}$
with
![]() $w_{d-1} h_d=g_{d+1}$
. As the bottom row is d-exact, there is an exact sequence
$w_{d-1} h_d=g_{d+1}$
. As the bottom row is d-exact, there is an exact sequence
Using the commutativity of the rightmost square, we get
![]() $w_{d-1}(g_d-h_de_d)=0$
, so
$w_{d-1}(g_d-h_de_d)=0$
, so
![]() $g_d-h_de_d$
is in the kernel of the second morphism. By exactness, there exists a morphism
$g_d-h_de_d$
is in the kernel of the second morphism. By exactness, there exists a morphism
![]() $h_{d-1}\colon E_d \to W_{d-2}$
such that
$h_{d-1}\colon E_d \to W_{d-2}$
such that
![]() $g_d-h_de_d = w_{d-2}h_{d-1}$
, or equivalently,
$g_d-h_de_d = w_{d-2}h_{d-1}$
, or equivalently,
![]() $g_d= h_d e_d + w_{d-2}h_{d-1}$
.
$g_d= h_d e_d + w_{d-2}h_{d-1}$
.
We can repeat this process to obtain a homotopy of the map of complexes g. In particular, there are morphisms
![]() $h_0$
and
$h_0$
and
![]() $h_1$
such that
$h_1$
such that
![]() $g_1 =1_{E_1} = \iota h_0 + h_1 e_1$
. This implies that
$g_1 =1_{E_1} = \iota h_0 + h_1 e_1$
. This implies that
![]() $\iota h_0 e_0 = e_0$
, so
$\iota h_0 e_0 = e_0$
, so
![]() $\iota h_0$
is an isomorphism by the left minimality of
$\iota h_0$
is an isomorphism by the left minimality of
![]() $e_0$
. The morphism
$e_0$
. The morphism
![]() $h_0$
is hence a split monomorphism, so
$h_0$
is hence a split monomorphism, so
![]() $E_1$
is contained in
$E_1$
is contained in
![]() $\mathcal {U}$
. By Lemma 3.10, this implies that
$\mathcal {U}$
. By Lemma 3.10, this implies that
![]() $E_i \in \mathcal {U}$
for
$E_i \in \mathcal {U}$
for
![]() $i=2,\dots ,d$
, so the subcategory
$i=2,\dots ,d$
, so the subcategory
![]() $\mathcal {U}$
is closed under minimal d-extensions.
$\mathcal {U}$
is closed under minimal d-extensions.
Remark 3.12. Proposition 3.11 implies that every d-torsion class is closed under d-cokernels.
The remainder of this subsection is devoted to proving the converse of Proposition 3.11. Since any d-torsion class in
![]() $\mathcal {M}$
is contravariantly finite in
$\mathcal {M}$
is contravariantly finite in
![]() $\mathcal {M}$
, we first establish that for a subcategory
$\mathcal {M}$
, we first establish that for a subcategory
![]() $\mathcal {U} \subseteq \mathcal {M}$
to be contravariantly finite, it is enough to assume closure under d-quotients.
$\mathcal {U} \subseteq \mathcal {M}$
to be contravariantly finite, it is enough to assume closure under d-quotients.
We first need a result on coimage factorisation in a d-cluster tilting subcategory. Recall from Section 2.1 that a morphism g in
![]() $\mathcal {M}$
is a weak cokernel if there exists a morphism f in
$\mathcal {M}$
is a weak cokernel if there exists a morphism f in
![]() $\mathcal {M}$
such that g is a weak cokernel of f.
$\mathcal {M}$
such that g is a weak cokernel of f.
Proposition 3.13. Let
![]() $f\colon M\to N$
be a morphism in
$f\colon M\to N$
be a morphism in
![]() $\mathcal {M}$
. Then there exists a factorisation
$\mathcal {M}$
. Then there exists a factorisation
![]() $f=f_2\circ f_1$
in
$f=f_2\circ f_1$
in
![]() $\mathcal {M}$
where
$\mathcal {M}$
where
![]() $f_2$
is a monomorphism and
$f_2$
is a monomorphism and
![]() $f_1$
is a composite of left minimal weak cokernels.
$f_1$
is a composite of left minimal weak cokernels.
Proof. Let
![]() $E_0$
denote the image of f, and let
$E_0$
denote the image of f, and let
![]() $\iota _0\colon E_0\to M_0$
be a minimal left
$\iota _0\colon E_0\to M_0$
be a minimal left
![]() $\mathcal {M}$
-approximation. The inclusion
$\mathcal {M}$
-approximation. The inclusion
![]() $E_0\to N$
lifts via
$E_0\to N$
lifts via
![]() $\iota _0$
to a morphism
$\iota _0$
to a morphism
![]() $g_0\colon M_0\to N$
. Let
$g_0\colon M_0\to N$
. Let
![]() $E_1$
be the image of
$E_1$
be the image of
![]() $g_0$
, and note that
$g_0$
, and note that
![]() $E_0\subseteq E_1$
. Repeating this procedure, we get a subobject
$E_0\subseteq E_1$
. Repeating this procedure, we get a subobject
![]() $E_i\subseteq N$
, a minimal left approximation
$E_i\subseteq N$
, a minimal left approximation
![]() $\iota _i\colon E_i\to M_i$
, and a lift
$\iota _i\colon E_i\to M_i$
, and a lift
![]() $g_i\colon M_i\to N$
for each
$g_i\colon M_i\to N$
for each
![]() $i\geq 0$
. In particular, the
$i\geq 0$
. In particular, the
![]() $E_i$
’s form an increasing sequence
$E_i$
’s form an increasing sequence
![]() $E_0\subseteq E_1\subseteq E_2\subseteq \cdots \subseteq E_i\subseteq \cdots $
of subobjects of N.
$E_0\subseteq E_1\subseteq E_2\subseteq \cdots \subseteq E_i\subseteq \cdots $
of subobjects of N.
Since
![]() $\mathcal {A}$
is of finite length, this sequence has to stabilise, say at
$\mathcal {A}$
is of finite length, this sequence has to stabilise, say at
![]() $E_j$
. This implies that the image of
$E_j$
. This implies that the image of
![]() $g_j\colon M_j\to N$
is
$g_j\colon M_j\to N$
is
![]() $E_j$
. But then the inclusion
$E_j$
. But then the inclusion
![]() $\iota _j\colon E_j\rightarrow M_j$
is a split monomorphism, and hence an isomorphism since it is also left minimal. This shows that
$\iota _j\colon E_j\rightarrow M_j$
is a split monomorphism, and hence an isomorphism since it is also left minimal. This shows that
![]() $E_j\in \mathcal {M}$
. Now let
$E_j\in \mathcal {M}$
. Now let
![]() $f_2\colon E_j\to N$
be the inclusion, and let
$f_2\colon E_j\to N$
be the inclusion, and let
![]() $f_1\colon M\to E_j$
be the composite
$f_1\colon M\to E_j$
be the composite
![]() $M\to E_0\rightarrow E_j$
. Note that this is equal to the composite
$M\to E_0\rightarrow E_j$
. Note that this is equal to the composite

By construction, the morphisms
![]() $M\to M_0$
and
$M\to M_0$
and
![]() $M_i\to M_{i+1}$
for
$M_i\to M_{i+1}$
for
![]() $i=0,\ldots , j-1$
are left minimal weak cokernels. Since
$i=0,\ldots , j-1$
are left minimal weak cokernels. Since
![]() $f_1$
is a composite of such morphisms and the isomorphism
$f_1$
is a composite of such morphisms and the isomorphism
![]() $M_j\cong E_j$
, this proves the claim.
$M_j\cong E_j$
, this proves the claim.
Lemma 3.14. Let
![]() $\mathcal {U}\subseteq \mathcal {M}$
be closed under d-quotients. If
$\mathcal {U}\subseteq \mathcal {M}$
be closed under d-quotients. If
![]() $g\colon M\to N$
is a left minimal weak cokernel with
$g\colon M\to N$
is a left minimal weak cokernel with
![]() $M\in \mathcal {U}$
, then
$M\in \mathcal {U}$
, then
![]() $N\in \mathcal {U}$
.
$N\in \mathcal {U}$
.
Proof. Assume g is a weak cokernel of a morphism f. Then g is part of a d-cokernel of f, and if g is left minimal, then it is part of the minimal d-cokernel of f; see Construction 2.9. This proves the claim.
We now apply Proposition 3.13 and Lemma 3.14 to show that being closed under d-quotients implies being contravariantly finite.
Proposition 3.15. Let
![]() $\mathcal {U} \subseteq \mathcal {M}$
be closed under d-quotients and consider
$\mathcal {U} \subseteq \mathcal {M}$
be closed under d-quotients and consider
![]() $M\in \mathcal {M}$
. Then there exists a minimal right
$M\in \mathcal {M}$
. Then there exists a minimal right
![]() $\mathcal {U}$
-approximation
$\mathcal {U}$
-approximation
![]() $U\to M$
which is a monomorphism. In particular, the subcategory
$U\to M$
which is a monomorphism. In particular, the subcategory
![]() $\mathcal {U}$
is contravariantly finite in
$\mathcal {U}$
is contravariantly finite in
![]() $\mathcal {A}$
.
$\mathcal {A}$
.
Proof. Consider the set of subobjects
![]() $U\subseteq M$
with
$U\subseteq M$
with
![]() $U\in \mathcal {U}$
. Note that this set is nonempty since
$U\in \mathcal {U}$
. Note that this set is nonempty since
![]() $0\in \mathcal {U}$
.
$0\in \mathcal {U}$
.
We first prove that this set has a unique maximal element. Indeed, since
![]() $\mathcal {A}$
has finite length, we can choose
$\mathcal {A}$
has finite length, we can choose
![]() $U\subseteq M$
with
$U\subseteq M$
with
![]() $U\in \mathcal {U}$
and where U is of maximal length with this property. Now let
$U\in \mathcal {U}$
and where U is of maximal length with this property. Now let
![]() $V\subseteq M$
with
$V\subseteq M$
with
![]() $V\in \mathcal {U}$
, and consider the induced morphism U ⊕ V → M. By Proposition 3.13, there exists
$V\in \mathcal {U}$
, and consider the induced morphism U ⊕ V → M. By Proposition 3.13, there exists
![]() $W\subseteq M$
with
$W\subseteq M$
with
![]() $W\in \mathcal {M}$
such that
$W\in \mathcal {M}$
such that
![]() $U\subseteq W\subseteq M$
and
$U\subseteq W\subseteq M$
and
![]() $V\subseteq W\subseteq M$
, and such that the induced morphism
$V\subseteq W\subseteq M$
, and such that the induced morphism
![]() $U\oplus V\to W$
is a composite of left minimal weak cokernels. Since
$U\oplus V\to W$
is a composite of left minimal weak cokernels. Since
![]() $\mathcal {U}$
is closed under d-quotients, it follows from Lemma 3.14 that
$\mathcal {U}$
is closed under d-quotients, it follows from Lemma 3.14 that
![]() $W\in \mathcal {U}$
. But since U is maximal with respect to the property that
$W\in \mathcal {U}$
. But since U is maximal with respect to the property that
![]() $U\in \mathcal {U}$
and
$U\in \mathcal {U}$
and
![]() $U\subseteq M$
, it follows that
$U\subseteq M$
, it follows that
![]() $U=W$
. This implies that V must be contained in U, and hence, U is the unique maximal subobject
$U=W$
. This implies that V must be contained in U, and hence, U is the unique maximal subobject
![]() $U\subseteq M$
satisfying
$U\subseteq M$
satisfying
![]() $U\in \mathcal {U}$
.
$U\in \mathcal {U}$
.
Now let
![]() $U'\to M$
be an arbitrary morphism with
$U'\to M$
be an arbitrary morphism with
![]() $U'\in \mathcal {U}$
. By Proposition 3.13, there exists an object
$U'\in \mathcal {U}$
. By Proposition 3.13, there exists an object
![]() $V'$
such that
$V'$
such that
![]() $U'\to M$
factors through
$U'\to M$
factors through
![]() $V'$
and where the morphism
$V'$
and where the morphism
![]() $U'\rightarrow V'$
is a composite of left minimal weak cokernels and the morphism
$U'\rightarrow V'$
is a composite of left minimal weak cokernels and the morphism
![]() $V'\rightarrow M$
is a monomorphism. It follows that
$V'\rightarrow M$
is a monomorphism. It follows that
![]() $V'\in \mathcal {U}$
and
$V'\in \mathcal {U}$
and
![]() $V'$
is a subobject of M.
$V'$
is a subobject of M.
By the maximality of U, we get that
![]() $V'\subseteq U\subseteq M$
, so the morphism
$V'\subseteq U\subseteq M$
, so the morphism
![]() $U'\to M$
also factors through U. This shows that the inclusion
$U'\to M$
also factors through U. This shows that the inclusion
![]() $U\subseteq M$
is a right
$U\subseteq M$
is a right
![]() $\mathcal {U}$
-approximation, which is minimal since it is a monomorphism. This proves the first claim.
$\mathcal {U}$
-approximation, which is minimal since it is a monomorphism. This proves the first claim.
Finally, the fact that
![]() $\mathcal {U}$
is contravariantly finite in
$\mathcal {U}$
is contravariantly finite in
![]() $\mathcal {A}$
follows from the fact that
$\mathcal {A}$
follows from the fact that
![]() $\mathcal {M}$
is contravariantly finite in
$\mathcal {M}$
is contravariantly finite in
![]() $\mathcal {A}$
and
$\mathcal {A}$
and
![]() $\mathcal {U}$
is contravariantly finite in
$\mathcal {U}$
is contravariantly finite in
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
Using the proposition above, we now show the converse of Proposition 3.11.
Proposition 3.16. Let
![]() $\mathcal {U} \subseteq \mathcal {M}$
be closed under d-extensions and d-quotients. Then
$\mathcal {U} \subseteq \mathcal {M}$
be closed under d-extensions and d-quotients. Then
![]() $\mathcal {U}$
is a d-torsion class in
$\mathcal {U}$
is a d-torsion class in
![]() $\mathcal {M}$
.
$\mathcal {M}$
.
Proof. Consider an object
![]() $M \in \mathcal {M}$
. By the definition of a d-torsion class (see Definition 2.13), we need to show that there exists a d-exact sequence
$M \in \mathcal {M}$
. By the definition of a d-torsion class (see Definition 2.13), we need to show that there exists a d-exact sequence
where
![]() $U_M\in \mathcal {U}$
and the sequence
$U_M\in \mathcal {U}$
and the sequence
![]() $0 \rightarrow \operatorname {Hom}_{\mathcal {M}}(U,V_1) \rightarrow \cdots \rightarrow \operatorname {Hom}_{\mathcal {M}}(U,V_d) \rightarrow 0$
is exact for every U in
$0 \rightarrow \operatorname {Hom}_{\mathcal {M}}(U,V_1) \rightarrow \cdots \rightarrow \operatorname {Hom}_{\mathcal {M}}(U,V_d) \rightarrow 0$
is exact for every U in
![]() $\mathcal {U}$
.
$\mathcal {U}$
.
Since
![]() $\mathcal {U}$
is closed under d-quotients, Proposition 3.15 shows that we may take a minimal right
$\mathcal {U}$
is closed under d-quotients, Proposition 3.15 shows that we may take a minimal right
![]() $\mathcal {U}$
-approximation
$\mathcal {U}$
-approximation
![]() $f \colon U_M \to M$
which is a monomorphism. Taking the minimal d-cokernel of f gives a d-exact sequence
$f \colon U_M \to M$
which is a monomorphism. Taking the minimal d-cokernel of f gives a d-exact sequence
Let
![]() $U\in \mathcal {U}$
. As f is a right
$U\in \mathcal {U}$
. As f is a right
![]() $\mathcal {U}$
-approximation, we know that
$\mathcal {U}$
-approximation, we know that
![]() $\operatorname {Hom}_{\mathcal {M}}(U,f)$
is an epimorphism. Thus, it follows from d-exactness of the sequence (4) that
$\operatorname {Hom}_{\mathcal {M}}(U,f)$
is an epimorphism. Thus, it follows from d-exactness of the sequence (4) that
is exact. To finish our proof, we hence need to show that the rightmost morphism in this sequence is an epimorphism.
Consider
![]() $h_d\in \operatorname {Hom}_{\mathcal {M}}(U,V_d)$
and take a d-pullback of (4) along
$h_d\in \operatorname {Hom}_{\mathcal {M}}(U,V_d)$
and take a d-pullback of (4) along
![]() $h_d$
. This yields a commutative diagram
$h_d$
. This yields a commutative diagram

where the upper row is a d-exact sequence. By the dual of Lemma 2.10, this d-extension can be assumed to be minimal, and then closedness of
![]() $\mathcal {U}$
under d-extensions implies
$\mathcal {U}$
under d-extensions implies
![]() $W_i\in \mathcal {U}$
for all
$W_i\in \mathcal {U}$
for all
![]() $i=0,\ldots ,d-1$
by Lemma 3.8. As f is a right
$i=0,\ldots ,d-1$
by Lemma 3.8. As f is a right
![]() $\mathcal {U}$
-approximation, the morphism
$\mathcal {U}$
-approximation, the morphism
![]() $h_0$
factors through f, so
$h_0$
factors through f, so
![]() $f_0$
is a split monomorphism. It follows, by [Reference JassoJ2, Proposition 2.6] and its dual, that
$f_0$
is a split monomorphism. It follows, by [Reference JassoJ2, Proposition 2.6] and its dual, that
![]() $f_d$
is a split epimorphism, and hence,
$f_d$
is a split epimorphism, and hence,
![]() $h_d$
factors through
$h_d$
factors through
![]() $V_{d-1}$
. In particular, the morphism
$V_{d-1}$
. In particular, the morphism
![]() $\operatorname {Hom}_{\mathcal {M}}(U,V_{d-1}) \rightarrow \operatorname {Hom}_{\mathcal {M}}(U,V_d)$
is an epimorphism, as required.
$\operatorname {Hom}_{\mathcal {M}}(U,V_{d-1}) \rightarrow \operatorname {Hom}_{\mathcal {M}}(U,V_d)$
is an epimorphism, as required.
We can now generalise the classical characterisation of torsion classes; cf. Theorem 2.12. Recall our standing assumption that subcategories are closed under direct summands.
Theorem 3.17. Let
![]() $\mathcal {M}$
be a d-cluster tilting subcategory of
$\mathcal {M}$
be a d-cluster tilting subcategory of
![]() $\mathcal {A}$
. A subcategory
$\mathcal {A}$
. A subcategory
![]() $\mathcal {U} \subseteq \mathcal {M}$
is a d-torsion class if and only if it is closed under both d-extensions and d-quotients.
$\mathcal {U} \subseteq \mathcal {M}$
is a d-torsion class if and only if it is closed under both d-extensions and d-quotients.
Proof. The necessity follows from Proposition 3.11, while the sufficiency follows from Proposition 3.16.
We now demonstrate the use of Theorem 3.17 in our running example.
Example 3.18. Let A and
![]() $\mathcal {M}$
be as described in Example 2.4. In Example 2.16, we claimed that
$\mathcal {M}$
be as described in Example 2.4. In Example 2.16, we claimed that
![]() $\mathcal {T}_1= \operatorname {add}\left \{{\tiny \begin {matrix} 3 \end {matrix}}\oplus {\tiny \begin {matrix} 1 \end {matrix}} \right \}$
and
$\mathcal {T}_1= \operatorname {add}\left \{{\tiny \begin {matrix} 3 \end {matrix}}\oplus {\tiny \begin {matrix} 1 \end {matrix}} \right \}$
and
![]() $\mathcal {T}_2 = \operatorname {add}\left \{{\tiny \begin {matrix} 3 \end {matrix}}\oplus {\tiny \begin {matrix} 2\\3 \end {matrix}}\oplus {\tiny \begin {matrix} 2 \end {matrix}} \right \}$
are torsion classes for which
$\mathcal {T}_2 = \operatorname {add}\left \{{\tiny \begin {matrix} 3 \end {matrix}}\oplus {\tiny \begin {matrix} 2\\3 \end {matrix}}\oplus {\tiny \begin {matrix} 2 \end {matrix}} \right \}$
are torsion classes for which
![]() $\mathcal {T}_1\cap \mathcal {M}= \operatorname {add}\left \{{\tiny \begin {matrix} 3 \end {matrix}}\oplus {\tiny \begin {matrix} 1 \end {matrix}} \right \}$
and
$\mathcal {T}_1\cap \mathcal {M}= \operatorname {add}\left \{{\tiny \begin {matrix} 3 \end {matrix}}\oplus {\tiny \begin {matrix} 1 \end {matrix}} \right \}$
and
![]() $\mathcal {T}_2\cap \mathcal {M} = \operatorname {add}\left \{{\tiny \begin {matrix} 3 \end {matrix}}\oplus {\tiny \begin {matrix} 2\\3 \end {matrix}}\right \}$
are not
$\mathcal {T}_2\cap \mathcal {M} = \operatorname {add}\left \{{\tiny \begin {matrix} 3 \end {matrix}}\oplus {\tiny \begin {matrix} 2\\3 \end {matrix}}\right \}$
are not
![]() $2$
-torsion classes in
$2$
-torsion classes in
![]() $\mathcal {M}$
. We now use Theorem 3.17 to explain why this is the case.
$\mathcal {M}$
. We now use Theorem 3.17 to explain why this is the case.
Consider the exact sequence
It is straightforward to check that this is a minimal
![]() $2$
-extension in
$2$
-extension in
![]() $\mathcal {M}$
. This implies that
$\mathcal {M}$
. This implies that
![]() $\mathcal {T}_1\cap \mathcal {M}$
is not closed under
$\mathcal {T}_1\cap \mathcal {M}$
is not closed under
![]() $2$
-extensions, so it is not a
$2$
-extensions, so it is not a
![]() $2$
-torsion class in
$2$
-torsion class in
![]() $\mathcal {M}$
by Theorem 3.17.
$\mathcal {M}$
by Theorem 3.17.
Similarly, using the same sequence, one can see that
![]() $\mathcal {T}_2 \cap \mathcal {M}$
is not closed under
$\mathcal {T}_2 \cap \mathcal {M}$
is not closed under
![]() $2$
-quotients. Therefore, Theorem 3.17 implies that
$2$
-quotients. Therefore, Theorem 3.17 implies that
![]() $\mathcal {T}_2\cap \mathcal {M}$
is not a
$\mathcal {T}_2\cap \mathcal {M}$
is not a
![]() $2$
-torsion class.
$2$
-torsion class.
A d-exact category is a pair
![]() $(\mathcal {C},\mathcal {X})$
consisting of an additive category
$(\mathcal {C},\mathcal {X})$
consisting of an additive category
![]() $\mathcal {C}$
and a class
$\mathcal {C}$
and a class
![]() $\mathcal {X}$
of d-exact sequences in
$\mathcal {X}$
of d-exact sequences in
![]() $\mathcal {C}$
satisfying certain axioms; see [Reference JassoJ2, Definition 4.2]. One immediate consequence of our characterisation result is that any d-torsion class
$\mathcal {C}$
satisfying certain axioms; see [Reference JassoJ2, Definition 4.2]. One immediate consequence of our characterisation result is that any d-torsion class
![]() $\mathcal {U}$
in
$\mathcal {U}$
in
![]() $\mathcal {M}$
carries the structure of a d-exact category.
$\mathcal {M}$
carries the structure of a d-exact category.
Corollary 3.19. Let
![]() $\mathcal {U} \subseteq \mathcal {M}$
be a d-torsion class. Consider the class
$\mathcal {U} \subseteq \mathcal {M}$
be a d-torsion class. Consider the class
![]() $\mathcal {X}$
of d-exact sequences in
$\mathcal {X}$
of d-exact sequences in
![]() $\mathcal {M}$
where all the terms are in
$\mathcal {M}$
where all the terms are in
![]() $\mathcal {U}$
. Then
$\mathcal {U}$
. Then
![]() $(\mathcal {U},\mathcal {X})$
is a d-exact category.
$(\mathcal {U},\mathcal {X})$
is a d-exact category.
Proof. By Theorem 3.17, the subcategory
![]() $\mathcal {U}$
is closed under d-extensions in
$\mathcal {U}$
is closed under d-extensions in
![]() $\mathcal {M}$
. The result hence follows by applying [Reference KlapprothKl, Corollary 4.15].
$\mathcal {M}$
. The result hence follows by applying [Reference KlapprothKl, Corollary 4.15].
Note that when viewing
![]() $\mathcal {M}$
and
$\mathcal {M}$
and
![]() $\mathcal {U}$
as d-exangulated categories – see [Reference Herschend, Liu and NakaokaHLN1] – Corollary 3.19 moreover implies that
$\mathcal {U}$
as d-exangulated categories – see [Reference Herschend, Liu and NakaokaHLN1] – Corollary 3.19 moreover implies that
![]() $\mathcal {U}$
is a d-exangulated subcategory of
$\mathcal {U}$
is a d-exangulated subcategory of
![]() $\mathcal {M}$
in the sense of [Reference HauglandH, Definition 3.7].
$\mathcal {M}$
in the sense of [Reference HauglandH, Definition 3.7].
3.3 Closure under d-extensions
To check if a subcategory
![]() $\mathcal {U} \subseteq \mathcal {M}$
is closed under d-extensions, it is necessary to determine the middle terms of any minimal d-extension between any two (not necessarily indecomposable) objects in
$\mathcal {U} \subseteq \mathcal {M}$
is closed under d-extensions, it is necessary to determine the middle terms of any minimal d-extension between any two (not necessarily indecomposable) objects in
![]() $\mathcal {U}$
. In this subsection, we show that under certain conditions, it is enough to understand the d-extensions between indecomposable objects. The main result is the following.
$\mathcal {U}$
. In this subsection, we show that under certain conditions, it is enough to understand the d-extensions between indecomposable objects. The main result is the following.
Theorem 3.20. Suppose
![]() $\mathcal {U} \subseteq \mathcal {M}$
is closed under d-extensions with indecomposable end terms and all d-quotients. Then
$\mathcal {U} \subseteq \mathcal {M}$
is closed under d-extensions with indecomposable end terms and all d-quotients. Then
![]() $\mathcal {U}$
is closed under all d-extensions.
$\mathcal {U}$
is closed under all d-extensions.
We apply the theorem above in Sections 5 and 6, where we use it to give a combinatorial description of d-torsion classes of higher Auslander algebras of type
![]() $\mathbb A$
and higher Nakayama algebras of type
$\mathbb A$
and higher Nakayama algebras of type
![]() $\mathbb {A}$
and
$\mathbb {A}$
and
![]() $\mathbb {A}_\infty ^\infty $
.
$\mathbb {A}_\infty ^\infty $
.
In order to prove Theorem 3.20, recall first from Lemma 3.8 that we may focus our attention purely on minimal d-extensions and minimal d-quotients. Our first step is to show that when closing a subcategory under d-extensions, it may suffice to consider d-extensions where the first term is indecomposable.
Lemma 3.21. Suppose
![]() $\mathcal {U} \subseteq \mathcal {M}$
is closed under d-quotients. If
$\mathcal {U} \subseteq \mathcal {M}$
is closed under d-quotients. If
![]() $\mathcal {U}$
is closed under d-extensions with indecomposable first term, then
$\mathcal {U}$
is closed under d-extensions with indecomposable first term, then
![]() $\mathcal {U}$
is closed under all d-extensions.
$\mathcal {U}$
is closed under all d-extensions.
Proof. Assume that
![]() $\mathcal {U}$
is closed under d-quotients and under d-extensions with indecomposable first term. Let
$\mathcal {U}$
is closed under d-quotients and under d-extensions with indecomposable first term. Let
be a minimal d-extension with
![]() $X,Y\in \mathcal {U}$
. We want to show that
$X,Y\in \mathcal {U}$
. We want to show that
![]() $E_i \in \mathcal {U}$
for all
$E_i \in \mathcal {U}$
for all
![]() $i=1,\dots ,d$
. By Lemma 3.10, it is sufficient to check that
$i=1,\dots ,d$
. By Lemma 3.10, it is sufficient to check that
![]() $E_1\in \mathcal {U}$
.
$E_1\in \mathcal {U}$
.
If X is indecomposable, we are done by assumption. Suppose, hence, that
![]() $X=X_1\oplus X_2$
, where
$X=X_1\oplus X_2$
, where
![]() $X_1$
is indecomposable and
$X_1$
is indecomposable and
![]() $X_2 \neq 0$
. We take a d-pushout of the d-extension along the projection
$X_2 \neq 0$
. We take a d-pushout of the d-extension along the projection
![]() $\pi \colon X\rightarrow X_1$
. This yields a commutative diagram
$\pi \colon X\rightarrow X_1$
. This yields a commutative diagram

where the lower sequence is d-exact and can be assumed to be minimal by Lemma 2.10. As
![]() $X_1$
is indecomposable, we have
$X_1$
is indecomposable, we have
![]() $F_i\in \mathcal {U}$
for
$F_i\in \mathcal {U}$
for
![]() $1\leq i\leq d$
. By [Reference JassoJ2, Proposition 4.8 (ii)], we have a d-exact sequence
$1\leq i\leq d$
. By [Reference JassoJ2, Proposition 4.8 (ii)], we have a d-exact sequence
Since
![]() $X\cong X_1\oplus X_2$
, this complex can be written as the sum of the identity morphism
$X\cong X_1\oplus X_2$
, this complex can be written as the sum of the identity morphism
and a d-exact sequence
Next, we choose a decomposition
![]() $E_1\cong E_1"\oplus E_1'$
and
$E_1\cong E_1"\oplus E_1'$
and
![]() $F_1\cong E_1^{\prime \prime }\oplus \tilde {F_1}$
such that the morphism
$F_1\cong E_1^{\prime \prime }\oplus \tilde {F_1}$
such that the morphism
![]() $E_1\to F_1$
becomes
$E_1\to F_1$
becomes
 $$ \begin{align*} \begin{pmatrix} 1_{E_1"} & 0 \\ 0 & f \end{pmatrix}\colon E_1"\oplus E_1' \rightarrow E_1"\oplus \tilde{F_1} \end{align*} $$
$$ \begin{align*} \begin{pmatrix} 1_{E_1"} & 0 \\ 0 & f \end{pmatrix}\colon E_1"\oplus E_1' \rightarrow E_1"\oplus \tilde{F_1} \end{align*} $$
with
![]() $f \in \operatorname {Rad}_{\mathcal {A}}(E_1', \tilde {F_1})$
. In particular,
$f \in \operatorname {Rad}_{\mathcal {A}}(E_1', \tilde {F_1})$
. In particular,
![]() $E_1"$
is a summand of
$E_1"$
is a summand of
![]() $F_1$
and is therefore contained in
$F_1$
and is therefore contained in
![]() $\mathcal {U}$
. Hence,
$\mathcal {U}$
. Hence,
![]() $E_1'\in \mathcal {U}$
if and only if
$E_1'\in \mathcal {U}$
if and only if
![]() $E_1\in \mathcal {U}$
. Furthermore, (6) can be written as a sum of the identity morphism
$E_1\in \mathcal {U}$
. Furthermore, (6) can be written as a sum of the identity morphism
and a d-exact sequence
By minimality of (5), the morphism
![]() $E_1\to E_2$
is in the Jacobson radical, and hence, the induced morphism
$E_1\to E_2$
is in the Jacobson radical, and hence, the induced morphism
![]() $E_1'\to E_2$
is also in the Jacobson radical. Combining this with the fact that
$E_1'\to E_2$
is also in the Jacobson radical. Combining this with the fact that
![]() $f\colon E_1'\to \tilde {F_1}$
is in the Jacobson radical, we get that
$f\colon E_1'\to \tilde {F_1}$
is in the Jacobson radical, we get that
![]() $E_1'\to \tilde {F_1'}\oplus E_2$
is in the Jacobson radical. Hence, if we let
$E_1'\to \tilde {F_1'}\oplus E_2$
is in the Jacobson radical. Hence, if we let
be the minimal d-cokernel of
![]() $X_2\to E_1'$
, then this must also give a minimal d-extension. By Proposition 2.6, the term
$X_2\to E_1'$
, then this must also give a minimal d-extension. By Proposition 2.6, the term
![]() $F^{\prime }_d$
is a direct summand of
$F^{\prime }_d$
is a direct summand of
![]() $F_d$
and must therefore be in
$F_d$
and must therefore be in
![]() $\mathcal {U}$
. Obviously, the object
$\mathcal {U}$
. Obviously, the object
![]() $X_2$
has fewer indecomposable summands than X. If
$X_2$
has fewer indecomposable summands than X. If
![]() $X_2$
is indecomposable, we know that
$X_2$
is indecomposable, we know that
![]() $E^{\prime }_1\in \mathcal {U}$
(which is equivalent to
$E^{\prime }_1\in \mathcal {U}$
(which is equivalent to
![]() $E_1\in \mathcal {U}$
), as the end terms
$E_1\in \mathcal {U}$
), as the end terms
![]() $X_2$
and
$X_2$
and
![]() $F_d'$
of the above minimal d-extension are in
$F_d'$
of the above minimal d-extension are in
![]() $\mathcal {U}$
. If not, we repeat the argument to eventually show that
$\mathcal {U}$
. If not, we repeat the argument to eventually show that
![]() $E_1\in \mathcal {U}$
.
$E_1\in \mathcal {U}$
.
We are now ready to give the proof of Theorem 3.20.
Proof of Theorem 3.20.
Suppose that we have a minimal d-extension
with
![]() $X, Y \in \mathcal {U}$
. By Lemma 3.21, we may assume that X is indecomposable. Let
$X, Y \in \mathcal {U}$
. By Lemma 3.21, we may assume that X is indecomposable. Let
![]() $Y= \bigoplus _{j=1}^t Y_j$
, where each
$Y= \bigoplus _{j=1}^t Y_j$
, where each
![]() $Y_j$
is indecomposable. For each inclusion
$Y_j$
is indecomposable. For each inclusion
![]() $\iota _j \colon Y_j \to Y$
, consider a d-pullback diagram
$\iota _j \colon Y_j \to Y$
, consider a d-pullback diagram

By the dual of Lemma 2.10, the top d-extension can be chosen to be minimal. Consequently, each of the morphisms
![]() $f_{j,1}, \dots , f_{j,d-1}$
is in the Jacobson radical. Moreover, the middle objects
$f_{j,1}, \dots , f_{j,d-1}$
is in the Jacobson radical. Moreover, the middle objects
![]() $F_{j,1},\dots ,F_{j,d}$
are in
$F_{j,1},\dots ,F_{j,d}$
are in
![]() $\mathcal {U}$
since
$\mathcal {U}$
since
![]() $\mathcal {U}$
is closed under d-extensions between indecomposables.
$\mathcal {U}$
is closed under d-extensions between indecomposables.
Now look at the d-extension
 $$ \begin{align*} 0 \to \bigoplus_{j=1}^t X \xrightarrow{f_0} \bigoplus_{j=1}^t F_{j,1} \xrightarrow{f_1} \cdots \xrightarrow{f_{d-1}} \bigoplus_{j=1}^t F_{j,d} \xrightarrow{f_d} \bigoplus_{j=1}^t Y_j \to 0 \end{align*} $$
$$ \begin{align*} 0 \to \bigoplus_{j=1}^t X \xrightarrow{f_0} \bigoplus_{j=1}^t F_{j,1} \xrightarrow{f_1} \cdots \xrightarrow{f_{d-1}} \bigoplus_{j=1}^t F_{j,d} \xrightarrow{f_d} \bigoplus_{j=1}^t Y_j \to 0 \end{align*} $$
given by the direct sum of all the upper d-extensions obtained as in (7). Consider the induced map

with
![]() $h_i = \left (\begin {smallmatrix} h_{1,i} & \cdots & h_{t,i} \end {smallmatrix}\right )$
for
$h_i = \left (\begin {smallmatrix} h_{1,i} & \cdots & h_{t,i} \end {smallmatrix}\right )$
for
![]() $i = 0,\dots ,d$
. This is a d-pushout diagram by [Reference JassoJ2, Proposition 4.8], and thus, the associated mapping cone
$i = 0,\dots ,d$
. This is a d-pushout diagram by [Reference JassoJ2, Proposition 4.8], and thus, the associated mapping cone
 $$ \begin{align} 0 \to \bigoplus_{j=1}^t X \xrightarrow{\left(\begin{smallmatrix} h_0 \\ -f_0 \end{smallmatrix}\right)} X \oplus \bigoplus_{j=1}^t F_{j,1} \xrightarrow{\left(\begin{smallmatrix} e_0 & h_1 \\ 0 & -f_1 \end{smallmatrix}\right)} E_1 \oplus \bigoplus_{j=1}^t F_{j,2} \rightarrow \cdots \rightarrow E_d \to 0 \end{align} $$
$$ \begin{align} 0 \to \bigoplus_{j=1}^t X \xrightarrow{\left(\begin{smallmatrix} h_0 \\ -f_0 \end{smallmatrix}\right)} X \oplus \bigoplus_{j=1}^t F_{j,1} \xrightarrow{\left(\begin{smallmatrix} e_0 & h_1 \\ 0 & -f_1 \end{smallmatrix}\right)} E_1 \oplus \bigoplus_{j=1}^t F_{j,2} \rightarrow \cdots \rightarrow E_d \to 0 \end{align} $$
is a d-extension. Note that the term
![]() $X \oplus \bigoplus _{j=1}^t F_{j,1}$
lies in
$X \oplus \bigoplus _{j=1}^t F_{j,1}$
lies in
![]() $\mathcal {U}$
. If (8) is given by the minimal d-cokernel of the first morphism, we are hence done by closure under minimal d-quotients. So suppose this d-cokernel is not minimal. By Remark 2.7, it is then isomorphic to the direct sum of the minimal d-cokernel and shifted complexes of the form
$\mathcal {U}$
. If (8) is given by the minimal d-cokernel of the first morphism, we are hence done by closure under minimal d-quotients. So suppose this d-cokernel is not minimal. By Remark 2.7, it is then isomorphic to the direct sum of the minimal d-cokernel and shifted complexes of the form
![]() $N \xrightarrow {1} N$
. In particular, if
$N \xrightarrow {1} N$
. In particular, if
 $$ \begin{align*} X \oplus \bigoplus_{j=1}^t F_{j,1} \xrightarrow{\partial_1} M_1 \xrightarrow{\partial_2} M_2 \to \cdots \to M_d \to 0 \end{align*} $$
$$ \begin{align*} X \oplus \bigoplus_{j=1}^t F_{j,1} \xrightarrow{\partial_1} M_1 \xrightarrow{\partial_2} M_2 \to \cdots \to M_d \to 0 \end{align*} $$
is the minimal d-cokernel of
![]() $\left (\begin {smallmatrix} h_0 \\ -f_0 \end {smallmatrix}\right )$
, then there is a commutative diagram
$\left (\begin {smallmatrix} h_0 \\ -f_0 \end {smallmatrix}\right )$
, then there is a commutative diagram

where the vertical maps are isomorphisms. Since
![]() $e_1 \in \operatorname {Rad}_{\mathcal {A}}(E_1, E_2)$
, the morphism
$e_1 \in \operatorname {Rad}_{\mathcal {A}}(E_1, E_2)$
, the morphism
 $$ \begin{align*} \phi \circ \begin{pmatrix} e_1 \\ 0 \end{pmatrix}\colon E_1 \rightarrow M_2 \oplus N_1 \oplus N_2 \end{align*} $$
$$ \begin{align*} \phi \circ \begin{pmatrix} e_1 \\ 0 \end{pmatrix}\colon E_1 \rightarrow M_2 \oplus N_1 \oplus N_2 \end{align*} $$
also lies in the radical, and thus so does
 $$ \begin{align*} \phi \circ \begin{pmatrix} e_1 \\ 0 \end{pmatrix} =\begin{pmatrix} \partial_2 & 0 \\ 0 & 1 \\ 0 & 0 \end{pmatrix} \begin{pmatrix} a \\ c \end{pmatrix}= \begin{pmatrix} \partial_2\circ a \\ c \\ 0 \end{pmatrix}. \end{align*} $$
$$ \begin{align*} \phi \circ \begin{pmatrix} e_1 \\ 0 \end{pmatrix} =\begin{pmatrix} \partial_2 & 0 \\ 0 & 1 \\ 0 & 0 \end{pmatrix} \begin{pmatrix} a \\ c \end{pmatrix}= \begin{pmatrix} \partial_2\circ a \\ c \\ 0 \end{pmatrix}. \end{align*} $$
This shows that
![]() $c \in \operatorname {Rad}_{\mathcal {A}}(E_1, N_1 )$
. Now let
$c \in \operatorname {Rad}_{\mathcal {A}}(E_1, N_1 )$
. Now let
![]() $ \left (\begin {smallmatrix} \alpha & \beta \\ \gamma & \delta \end {smallmatrix}\right )$
denote the inverse of
$ \left (\begin {smallmatrix} \alpha & \beta \\ \gamma & \delta \end {smallmatrix}\right )$
denote the inverse of
![]() $\left (\begin {smallmatrix} a & b \\ c & d \end {smallmatrix}\right )$
. We have
$\left (\begin {smallmatrix} a & b \\ c & d \end {smallmatrix}\right )$
. We have
![]() $\alpha a + \beta c =1_{E_1}$
, or equivalently,
$\alpha a + \beta c =1_{E_1}$
, or equivalently,
![]() $\alpha a = 1_{E_1} - \beta c$
. It follows from the definition of the radical that this is an isomorphism, as
$\alpha a = 1_{E_1} - \beta c$
. It follows from the definition of the radical that this is an isomorphism, as
![]() $c \in \operatorname {Rad}_{\mathcal {A}}(E_1, N_1 )$
. This implies that
$c \in \operatorname {Rad}_{\mathcal {A}}(E_1, N_1 )$
. This implies that
![]() $E_1$
is a direct summand of
$E_1$
is a direct summand of
![]() $M_1$
. But
$M_1$
. But
![]() $M_1 \in \mathcal {U}$
since
$M_1 \in \mathcal {U}$
since
![]() $\mathcal {U}$
is closed under minimal d-quotients, and hence,
$\mathcal {U}$
is closed under minimal d-quotients, and hence,
![]() $E_1$
also lies in
$E_1$
also lies in
![]() $\mathcal {U}$
. It then follows from Lemma 3.10 that
$\mathcal {U}$
. It then follows from Lemma 3.10 that
![]() $E_2, \dots , E_d \in \mathcal {U} $
, so we can conclude that
$E_2, \dots , E_d \in \mathcal {U} $
, so we can conclude that
![]() $\mathcal {U}$
is closed under d-extensions as required.
$\mathcal {U}$
is closed under d-extensions as required.
4 The lattice of d-torsion classes
The torsion classes in
![]() $\mathcal {A}$
form a complete lattice with meet given by intersection; see, for example, [Reference Iyama, Reiten, Thomas and TodorovIRTT, Proposition 2.3]. In this section, we use the characterisation of higher torsion classes given in Theorem 3.17 to show that an analogous statement holds for higher torsion classes.
$\mathcal {A}$
form a complete lattice with meet given by intersection; see, for example, [Reference Iyama, Reiten, Thomas and TodorovIRTT, Proposition 2.3]. In this section, we use the characterisation of higher torsion classes given in Theorem 3.17 to show that an analogous statement holds for higher torsion classes.
Let us first recall some relevant definitions.
Definition 4.1. Let P be a poset. For an arbitrary subset
![]() $H \subseteq P$
, the join of H, if it exists, is the least upper bound of H. Dually, the meet of H, if it exists, is the greatest lower bound of H. The poset P is a complete lattice if for any subset
$H \subseteq P$
, the join of H, if it exists, is the least upper bound of H. Dually, the meet of H, if it exists, is the greatest lower bound of H. The poset P is a complete lattice if for any subset
![]() $H\subseteq P$
, the join and the meet of H exist.
$H\subseteq P$
, the join and the meet of H exist.
For the sake of clarity, note that a least upper bound is unique as it is smaller than any other upper bound, and similarly for greatest lower bounds. Note also that a complete lattice is bounded (i.e., it has a minimum and a maximum) obtained by letting H in the definition be empty. The following lemma is well known; see, for example, [Reference GrätzerG, Chapter I, Lemma 34].
Lemma 4.2. Let P be a poset. If every subset of P admits a meet or if every subset of P admits a join, then P is a complete lattice.
For a d-cluster tilting subcategory
![]() $\mathcal {M}$
of
$\mathcal {M}$
of
![]() $\mathcal {A}$
, we let
$\mathcal {A}$
, we let
![]() $d\text {-}\!\operatorname {tors}(\mathcal {M})$
denote the poset of d-torsion classes in
$d\text {-}\!\operatorname {tors}(\mathcal {M})$
denote the poset of d-torsion classes in
![]() $\mathcal {M}$
ordered by inclusion.
$\mathcal {M}$
ordered by inclusion.
Theorem 4.3. Let
![]() $\mathcal {M}$
be a d-cluster tilting subcategory of
$\mathcal {M}$
be a d-cluster tilting subcategory of
![]() $\mathcal {A}$
. Then
$\mathcal {A}$
. Then
![]() $d\text {-}\!\operatorname {tors}(\mathcal {M})$
is a complete lattice with meet given by intersection.
$d\text {-}\!\operatorname {tors}(\mathcal {M})$
is a complete lattice with meet given by intersection.
Proof. To show that
![]() $d\text {-}\!\operatorname {tors}(\mathcal {M})$
is a complete lattice, it suffices to show that it has arbitrary meets by Lemma 4.2. We note that if
$d\text {-}\!\operatorname {tors}(\mathcal {M})$
is a complete lattice, it suffices to show that it has arbitrary meets by Lemma 4.2. We note that if
![]() $d\text {-}\!\operatorname {tors}(\mathcal {M})$
is closed under arbitrary intersections, then meets are given by intersections, and closure under arbitrary meets follows. Therefore, we only need to show that for any subset S of
$d\text {-}\!\operatorname {tors}(\mathcal {M})$
is closed under arbitrary intersections, then meets are given by intersections, and closure under arbitrary meets follows. Therefore, we only need to show that for any subset S of
![]() $d\text {-}\!\operatorname {tors}(\mathcal {M})$
, the intersection
$d\text {-}\!\operatorname {tors}(\mathcal {M})$
, the intersection
is a d-torsion class. By Theorem 3.17 and Lemma 3.8, it is enough to show that
![]() $\mathcal {V}$
is closed under minimal d-extensions and minimal d-quotients. This follows from the fact that each
$\mathcal {V}$
is closed under minimal d-extensions and minimal d-quotients. This follows from the fact that each
![]() $\mathcal {U}\in S$
is closed under d-extensions and d-quotients by Theorem 3.17.
$\mathcal {U}\in S$
is closed under d-extensions and d-quotients by Theorem 3.17.
We illustrate the lattice structure on the set of higher torsion classes in our running example.
Example 4.4. In the setting of Example 2.4, the set of all
![]() $2$
-torsion classes in
$2$
-torsion classes in
![]() $\mathcal {M}$
is listed in Table 1. By Theorem 4.3, we know that the poset of all
$\mathcal {M}$
is listed in Table 1. By Theorem 4.3, we know that the poset of all
![]() $2$
-torsion classes in
$2$
-torsion classes in
![]() $\mathcal {M}$
ordered by inclusion forms a complete lattice. We include the Hasse diagram in Figure 2.
$\mathcal {M}$
ordered by inclusion forms a complete lattice. We include the Hasse diagram in Figure 2.

Figure 2 The Hasse diagram of the lattice of
![]() $2$
-torsion classes in Example 4.4.
$2$
-torsion classes in Example 4.4.
Another example – namely, the complete lattice of
![]() $3$
-torsion classes for the higher Auslander algebra
$3$
-torsion classes for the higher Auslander algebra
![]() $A_3^3$
– can be found in Example 5.21. This example will demonstrate that, unlike in the classical setting, the lattice of d-torsion classes may not be Hasse-regular or semi-distributive (see e.g. [Reference Demonet, Iyama, Reading, Reiten and ThomasDIRRT] for the definitions).
$A_3^3$
– can be found in Example 5.21. This example will demonstrate that, unlike in the classical setting, the lattice of d-torsion classes may not be Hasse-regular or semi-distributive (see e.g. [Reference Demonet, Iyama, Reading, Reiten and ThomasDIRRT] for the definitions).
It follows from Theorem 2.15 that there is an injective, order-preserving map
which takes a d-torsion class
![]() $\mathcal {U} \subseteq \mathcal {M}$
to the smallest torsion class in
$\mathcal {U} \subseteq \mathcal {M}$
to the smallest torsion class in
![]() $\mathcal {A}$
containing
$\mathcal {A}$
containing
![]() $\mathcal {U}$
(see [Reference Asadollahi, Jørgensen, Schroll and TreffingerAJST, Corollary 3.3]). We now give an example that demonstrates that this map is not a morphism of lattices.
$\mathcal {U}$
(see [Reference Asadollahi, Jørgensen, Schroll and TreffingerAJST, Corollary 3.3]). We now give an example that demonstrates that this map is not a morphism of lattices.
Example 4.5. Continuing with Example 4.4, we see that the
![]() $2$
-torsion classes
$2$
-torsion classes
![]() $\operatorname {add}\{3\}$
and
$\operatorname {add}\{3\}$
and
![]() $\operatorname {add}\{1\}$
are both torsion classes in
$\operatorname {add}\{1\}$
are both torsion classes in
![]() $\mathcal {A}$
and thus are sent to themselves under the map (9). However, Figure 2 shows that the join in
$\mathcal {A}$
and thus are sent to themselves under the map (9). However, Figure 2 shows that the join in
![]() $2$
-
$2$
-
![]() $\operatorname {tors}(\mathcal {M})$
is
$\operatorname {tors}(\mathcal {M})$
is
![]() $\mathcal {M}$
, which is sent to
$\mathcal {M}$
, which is sent to
![]() $\mathcal {A}$
under (9), while the join in
$\mathcal {A}$
under (9), while the join in
![]() $\operatorname {tors}(\mathcal {A})$
is simply
$\operatorname {tors}(\mathcal {A})$
is simply
![]() $\operatorname {add}\{3 \oplus 1\}$
, which is contained in
$\operatorname {add}\{3 \oplus 1\}$
, which is contained in
![]() $\mathcal {M}$
, but it is not a
$\mathcal {M}$
, but it is not a
![]() $2$
-torsion class.
$2$
-torsion class.
Remark 4.6. Note that for
![]() $\mathcal {U}\in d\text {-}\!\operatorname {tors}(\mathcal {M})$
, the set
$\mathcal {U}\in d\text {-}\!\operatorname {tors}(\mathcal {M})$
, the set
may contain more than one element, is convex and has a minimal element. Indeed, for the
![]() $2$
-torsion class
$2$
-torsion class ![]() in Example 4.5, we have
in Example 4.5, we have
and hence,
![]() $\operatorname {tors}_{\,\mathcal {U}}(\mathcal {A})$
has more than one element. Also, for
$\operatorname {tors}_{\,\mathcal {U}}(\mathcal {A})$
has more than one element. Also, for
![]() $\mathcal {U}\in d\text {-}\!\operatorname {tors}(\mathcal {M})$
, if we have inclusions
$\mathcal {U}\in d\text {-}\!\operatorname {tors}(\mathcal {M})$
, if we have inclusions
![]() $\mathcal {T}_1\subseteq \mathcal {T}\subseteq \mathcal {T}_2$
of torsion classes such that
$\mathcal {T}_1\subseteq \mathcal {T}\subseteq \mathcal {T}_2$
of torsion classes such that
![]() $\mathcal {T}_1,\mathcal {T}_2\in \operatorname {tors}_{\,\mathcal {U}}(\mathcal {A})$
, then
$\mathcal {T}_1,\mathcal {T}_2\in \operatorname {tors}_{\,\mathcal {U}}(\mathcal {A})$
, then
This shows that
![]() $\mathcal {T}\in \operatorname {tors}_{\,\mathcal {U}}(\mathcal {A})$
, and hence,
$\mathcal {T}\in \operatorname {tors}_{\,\mathcal {U}}(\mathcal {A})$
, and hence,
![]() $\operatorname {tors}_{\,\mathcal {U}} (\mathcal {A})$
is convex. Finally,
$\operatorname {tors}_{\,\mathcal {U}} (\mathcal {A})$
is convex. Finally,
![]() $T(\mathcal {U})$
is the minimal element in
$T(\mathcal {U})$
is the minimal element in
![]() $\operatorname {tors}_{\,\mathcal {U}}(\mathcal {A})$
by Theorem 2.15, where
$\operatorname {tors}_{\,\mathcal {U}}(\mathcal {A})$
by Theorem 2.15, where
![]() $\mathrm {T}(-)$
is as in (9).
$\mathrm {T}(-)$
is as in (9).
We finish by investigating when the intersection with a d-cluster tilting subcategory gives a map of posets. The result will be applied in the context of higher Nakayama algebras in Section 6.
Proposition 4.7. Let
![]() $\mathcal {A}_1$
and
$\mathcal {A}_1$
and
![]() $\mathcal {A}_2$
be abelian categories of finite length, and let
$\mathcal {A}_2$
be abelian categories of finite length, and let
![]() ${\mathcal {M}}_1\subseteq \mathcal {A}_1$
and
${\mathcal {M}}_1\subseteq \mathcal {A}_1$
and
![]() ${\mathcal {M}}_2\subseteq \mathcal {A}_2$
be d-cluster tilting subcategories. Assume we have an exact inclusion
${\mathcal {M}}_2\subseteq \mathcal {A}_2$
be d-cluster tilting subcategories. Assume we have an exact inclusion
![]() $\mathcal {A}_2 \subseteq \mathcal {A}_1$
such that
$\mathcal {A}_2 \subseteq \mathcal {A}_1$
such that
![]() ${\mathcal {M}}_2\subseteq {\mathcal {M}}_1$
. The following statements hold:
${\mathcal {M}}_2\subseteq {\mathcal {M}}_1$
. The following statements hold:
-
(1) If
 $\mathcal {U}$
is a d-torsion class in
$\mathcal {U}$
is a d-torsion class in
 ${\mathcal {M}}_1$
, then
${\mathcal {M}}_1$
, then
 $\mathcal {U}\cap {\mathcal {M}}_2$
is a d-torsion class in
$\mathcal {U}\cap {\mathcal {M}}_2$
is a d-torsion class in
 ${\mathcal {M}}_2$
.
${\mathcal {M}}_2$
. -
(2) Intersecting with
 ${\mathcal {M}}_2$
gives a map of posets which preserves meets.
${\mathcal {M}}_2$
gives a map of posets which preserves meets. $$\begin{align*}d\text{-}\!\operatorname{tors}({\mathcal{M}}_1)\to d\text{-}\!\operatorname{tors}({\mathcal{M}}_2) \end{align*}$$
$$\begin{align*}d\text{-}\!\operatorname{tors}({\mathcal{M}}_1)\to d\text{-}\!\operatorname{tors}({\mathcal{M}}_2) \end{align*}$$
-
(3) If
 $\mathcal {A}_2$
is closed under quotients in
$\mathcal {A}_2$
is closed under quotients in
 $\mathcal {A}_1$
, then
$\mathcal {A}_1$
, then
 ${\mathcal {M}}_2$
is closed under d-quotients in
${\mathcal {M}}_2$
is closed under d-quotients in
 ${\mathcal {M}}_1$
.
${\mathcal {M}}_1$
.
Proof. Assume that
![]() $\mathcal {U}$
is a d-torsion class in
$\mathcal {U}$
is a d-torsion class in
![]() ${\mathcal {M}}_1$
. Since the inclusion
${\mathcal {M}}_1$
. Since the inclusion
![]() $\mathcal {A}_2\subseteq \mathcal {A}_1$
is exact, it must send d-cokernels and d-kernels in
$\mathcal {A}_2\subseteq \mathcal {A}_1$
is exact, it must send d-cokernels and d-kernels in
![]() ${\mathcal {M}}_2$
to d-cokernels and d-kernels in
${\mathcal {M}}_2$
to d-cokernels and d-kernels in
![]() ${\mathcal {M}}_1$
, respectively. In particular, it preserves d-quotients and d-extensions. Therefore, the subcategory
${\mathcal {M}}_1$
, respectively. In particular, it preserves d-quotients and d-extensions. Therefore, the subcategory
![]() $\mathcal {U}\cap {\mathcal {M}}_2$
must be closed under d-extensions and d-quotients in
$\mathcal {U}\cap {\mathcal {M}}_2$
must be closed under d-extensions and d-quotients in
![]() ${\mathcal {M}}_2$
, since
${\mathcal {M}}_2$
, since
![]() $\mathcal {U}$
is closed under d-extensions and d-quotients in
$\mathcal {U}$
is closed under d-extensions and d-quotients in
![]() ${\mathcal {M}}_1$
. This proves (1).
${\mathcal {M}}_1$
. This proves (1).
Part (2) follows from (1) and the fact that meets in
![]() $d\text {-}\!\operatorname {tors}({\mathcal {M}}_1)$
and
$d\text {-}\!\operatorname {tors}({\mathcal {M}}_1)$
and
![]() $d\text {-}\!\operatorname {tors}(\mathcal {M}_2)$
are given by intersection.
$d\text {-}\!\operatorname {tors}(\mathcal {M}_2)$
are given by intersection.
For part (3), note that giving a d-quotient in
![]() ${\mathcal {M}}_1$
of an object
${\mathcal {M}}_1$
of an object
![]() $Y\in {\mathcal {M}}_2$
is the same as giving a d-cokernel in
$Y\in {\mathcal {M}}_2$
is the same as giving a d-cokernel in
![]() $\mathcal {M}_1$
of a morphism
$\mathcal {M}_1$
of a morphism
![]() $X\to Y$
with
$X\to Y$
with
![]() $X\in \mathcal {M}_1$
. This is again equivalent to giving an exact sequence
$X\in \mathcal {M}_1$
. This is again equivalent to giving an exact sequence
where C is the cokernel of
![]() $X\to Y$
and each
$X\to Y$
and each
![]() $M_i$
is in
$M_i$
is in
![]() ${\mathcal {M}}_1$
. Now since
${\mathcal {M}}_1$
. Now since
![]() $\mathcal {A}_2$
is closed under quotients in
$\mathcal {A}_2$
is closed under quotients in
![]() $\mathcal {A}_1$
, the cokernel C must be contained in
$\mathcal {A}_1$
, the cokernel C must be contained in
![]() $\mathcal {A}_2$
. As
$\mathcal {A}_2$
. As
![]() $\mathcal {M}_2$
is d-cluster tilting in
$\mathcal {M}_2$
is d-cluster tilting in
![]() $\mathcal {A}_2$
, we can construct an exact sequence
$\mathcal {A}_2$
, we can construct an exact sequence
where each
![]() $N_i$
is in
$N_i$
is in
![]() ${\mathcal {M}}_2$
; see [Reference JassoJ2, Proposition 3.17]. Since
${\mathcal {M}}_2$
; see [Reference JassoJ2, Proposition 3.17]. Since
![]() ${\mathcal {M}}_2\subseteq {\mathcal {M}}_1$
, this must give a d-cokernel of
${\mathcal {M}}_2\subseteq {\mathcal {M}}_1$
, this must give a d-cokernel of
![]() $X\to Y$
in
$X\to Y$
in
![]() ${\mathcal {M}}_1$
by the observation above. This proves the claim.
${\mathcal {M}}_1$
by the observation above. This proves the claim.
Remark 4.8. Note that if
![]() $\mathcal {A}_2$
is closed under quotients in
$\mathcal {A}_2$
is closed under quotients in
![]() $\mathcal {A}_1$
, it follows from Proposition 4.7(3) that any minimal d-cokernel in
$\mathcal {A}_1$
, it follows from Proposition 4.7(3) that any minimal d-cokernel in
![]() ${\mathcal {M}}_1$
of a morphism
${\mathcal {M}}_1$
of a morphism
![]() $X \to Y$
with
$X \to Y$
with
![]() $Y \in {\mathcal {M}}_2$
is a minimal d-cokernel of a morphism in
$Y \in {\mathcal {M}}_2$
is a minimal d-cokernel of a morphism in
![]() ${\mathcal {M}}_2$
. In particular, a subcategory of
${\mathcal {M}}_2$
. In particular, a subcategory of
![]() ${\mathcal {M}}_2$
is closed under d-quotients in
${\mathcal {M}}_2$
is closed under d-quotients in
![]() ${\mathcal {M}}_2$
if and only if it is closed under d-quotients in
${\mathcal {M}}_2$
if and only if it is closed under d-quotients in
![]() ${\mathcal {M}}_1$
.
${\mathcal {M}}_1$
.
5 Higher Auslander algebras
In this section, we apply Theorem 3.17 to classify and count the d-torsion classes associated to higher Auslander algebras of type
![]() $\mathbb A$
. Higher Auslander algebras were introduced in [Reference IyamaI3] and constitute an important class of algebras in higher homological algebra. The module category of each such algebra contains a d-cluster tilting subcategory, which was described combinatorially in [Reference IyamaI3] and [Reference Oppermann and ThomasOT].
$\mathbb A$
. Higher Auslander algebras were introduced in [Reference IyamaI3] and constitute an important class of algebras in higher homological algebra. The module category of each such algebra contains a d-cluster tilting subcategory, which was described combinatorially in [Reference IyamaI3] and [Reference Oppermann and ThomasOT].
Recall from Theorem 3.17 that d-torsion classes in a d-cluster tilting subcategory are precisely the subcategories which are closed under d-extensions and d-quotients. In Sections 5.1 and 5.2, we present results on closure under d-extensions and d-quotients for higher Auslander algebras of type
![]() $\mathbb A$
, culiminating in a combinatorial characterisation of their higher torsion classes in Theorem 5.13. In Section 5.3, we employ our results to write an algorithm which computes and counts all these d-torsion classes.
$\mathbb A$
, culiminating in a combinatorial characterisation of their higher torsion classes in Theorem 5.13. In Section 5.3, we employ our results to write an algorithm which computes and counts all these d-torsion classes.
5.1 Background on higher Auslander algebras
We start by providing a brief introduction to higher Auslander algebras, highlighting combinatorial descriptions which will be important throughout Section 5. We mostly follow the notation and terminology from [Reference Jasso, Külshammer, Psaroudakis and KvammeJKPK].
For positive integers n and d, let
![]() $N_n=\{0,1, \dots , n-1\}$
with the natural poset structure. Consider the set
$N_n=\{0,1, \dots , n-1\}$
with the natural poset structure. Consider the set
 $$\begin{align*}N_{n}^d = \underbrace{N_n\times\cdots\times N_n}_{d\text{ times}} \end{align*}$$
$$\begin{align*}N_{n}^d = \underbrace{N_n\times\cdots\times N_n}_{d\text{ times}} \end{align*}$$
of d-tuples
![]() $x=(x_0,\dots ,x_{d-1})$
over
$x=(x_0,\dots ,x_{d-1})$
over
![]() $N_n$
. We endow
$N_n$
. We endow
![]() $N_n^d$
with the product order, meaning that
$N_n^d$
with the product order, meaning that
![]() $x\leq y$
in
$x\leq y$
in
![]() $N_{n}^d$
if and only if
$N_{n}^d$
if and only if
![]() $x_i\leq y_i$
for all
$x_i\leq y_i$
for all
![]() $i=0, 1, \ldots , d-1$
. We consider
$i=0, 1, \ldots , d-1$
. We consider
![]() $N_n^d$
as a category whose objects are the elements of
$N_n^d$
as a category whose objects are the elements of
![]() $N_n^d$
, and whose morphisms are given by the poset relations of
$N_n^d$
, and whose morphisms are given by the poset relations of
![]() $N_n^d$
. Taking the
$N_n^d$
. Taking the
![]() $\mathbb {k}$
-linearisation of this category, we get a finite-dimensional
$\mathbb {k}$
-linearisation of this category, we get a finite-dimensional
![]() $\mathbb {k}$
-algebra; see [Reference Jasso, Külshammer, Psaroudakis and KvammeJKPK, Section 1.2] for more details. By abuse of notation, we also denote this algebra by
$\mathbb {k}$
-algebra; see [Reference Jasso, Külshammer, Psaroudakis and KvammeJKPK, Section 1.2] for more details. By abuse of notation, we also denote this algebra by
![]() $N_n^d$
.
$N_n^d$
.
Let
![]() $\operatorname {os}_n^d$
be the subset of
$\operatorname {os}_n^d$
be the subset of
![]() $N_n^d$
of non-decreasing d-tuples over
$N_n^d$
of non-decreasing d-tuples over
![]() $N_{n}$
. In particular, an element of
$N_{n}$
. In particular, an element of
![]() $\operatorname {os}_n^d$
is a tuple
$\operatorname {os}_n^d$
is a tuple
![]() $x=(x_0,\dots ,x_{d-1})$
with
$x=(x_0,\dots ,x_{d-1})$
with
![]() $x_{0}\leq x_{1}\leq \dots \leq x_{d-1}$
. The higher Auslander algebra
$x_{0}\leq x_{1}\leq \dots \leq x_{d-1}$
. The higher Auslander algebra
![]() $A_n^{d}$
is defined as the idempotent quotient
$A_n^{d}$
is defined as the idempotent quotient
where we consider
![]() $N_n^d$
as a finite-dimensional
$N_n^d$
as a finite-dimensional
![]() $\mathbb {k}$
-algebra as above. Note that
$\mathbb {k}$
-algebra as above. Note that
![]() $A_n^{d}$
is equivalently given by the opposite of a quiver
$A_n^{d}$
is equivalently given by the opposite of a quiver
![]() $Q^{n,d}$
whose vertices are the elements of the set
$Q^{n,d}$
whose vertices are the elements of the set
![]() $\operatorname {os}_n^d$
, and where there is an arrow from vertex x to vertex y if we have
$\operatorname {os}_n^d$
, and where there is an arrow from vertex x to vertex y if we have
![]() $y_i=x_i+1$
for exactly one
$y_i=x_i+1$
for exactly one
![]() $0\leq i\leq d-1$
and
$0\leq i\leq d-1$
and
![]() $y_j=x_j$
for
$y_j=x_j$
for
![]() $j\neq i$
. The relations of
$j\neq i$
. The relations of
![]() $A_n^{d}$
are given by an admissible ideal
$A_n^{d}$
are given by an admissible ideal
![]() $I_{n,d}$
making squares commutative and sending certain compositions of two arrows to zero; see [Reference Herschend and JørgensenHJ].
$I_{n,d}$
making squares commutative and sending certain compositions of two arrows to zero; see [Reference Herschend and JørgensenHJ].
Remark 5.1. The notation we use is similar to that in [Reference Jasso, Külshammer, Psaroudakis and KvammeJKPK]. It relates to the notation in [Reference Herschend and JørgensenHJ] in the following way: What we call
![]() $Q^{n,d}$
,
$Q^{n,d}$
,
![]() $A_n^d$
and
$A_n^d$
and
![]() $I_{n,d}$
corresponds to what is denoted by
$I_{n,d}$
corresponds to what is denoted by
![]() $Q^{n,d-1}$
,
$Q^{n,d-1}$
,
![]() $A_n^{d-1}$
and
$A_n^{d-1}$
and
![]() $I_{n,d-1}$
in [Reference Herschend and JørgensenHJ]. To see this, note that the poset
$I_{n,d-1}$
in [Reference Herschend and JørgensenHJ]. To see this, note that the poset
![]() $\operatorname {os}_n^d$
is isomorphic to the poset
$\operatorname {os}_n^d$
is isomorphic to the poset
![]() $\mathcal {V}_{n,d-1}$
of increasing d-tuples
$\mathcal {V}_{n,d-1}$
of increasing d-tuples
![]() $x'=(x^{\prime }_0,\dots ,x^{\prime }_{d-1})$
over
$x'=(x^{\prime }_0,\dots ,x^{\prime }_{d-1})$
over
![]() $\{1,2,\dots ,n+d-1\}$
used in [Reference Herschend and JørgensenHJ]. The isomorphism is given by
$\{1,2,\dots ,n+d-1\}$
used in [Reference Herschend and JørgensenHJ]. The isomorphism is given by
The module category of
![]() $A_n^d$
has a d-cluster tilting subcategory
$A_n^d$
has a d-cluster tilting subcategory
where
![]() $M^d_{n}=\bigoplus _{x\in \operatorname {os}_n^{d+1}} M_x$
. Here, the notation
$M^d_{n}=\bigoplus _{x\in \operatorname {os}_n^{d+1}} M_x$
. Here, the notation
![]() $M_x$
is used for the indecomposable
$M_x$
is used for the indecomposable
![]() $A_n^d$
-module with support in all vertices
$A_n^d$
-module with support in all vertices
![]() $y\in \operatorname {os}_n^d$
such that
$y\in \operatorname {os}_n^d$
such that
![]() $x_{0}\leq y_{0} \leq x_{1} \leq \cdots \leq x_{d-1} \leq y_{d-1} \leq x_{d} $
. Note that the d-cluster tilting subcategory
$x_{0}\leq y_{0} \leq x_{1} \leq \cdots \leq x_{d-1} \leq y_{d-1} \leq x_{d} $
. Note that the d-cluster tilting subcategory
![]() ${\mathcal {M}}_n^d$
contains finitely many indecomposable objects, indexed by
${\mathcal {M}}_n^d$
contains finitely many indecomposable objects, indexed by
![]() $\operatorname {os}_n^{d+1}$
. It is known that
$\operatorname {os}_n^{d+1}$
. It is known that
![]() $\operatorname {End}_{A_n^d}(M^d_{n})$
and
$\operatorname {End}_{A_n^d}(M^d_{n})$
and
![]() $A^{d+1}_{n}$
are isomorphic as algebras by [Reference IyamaI3, Corollary 1.16]; see also [Reference Jasso, Külshammer, Psaroudakis and KvammeJKPK, Theorem 2.3]. For examples of the quivers
$A^{d+1}_{n}$
are isomorphic as algebras by [Reference IyamaI3, Corollary 1.16]; see also [Reference Jasso, Külshammer, Psaroudakis and KvammeJKPK, Theorem 2.3]. For examples of the quivers
![]() $Q^{n,d}$
and relevant modules, see [Reference Jasso, Külshammer, Psaroudakis and KvammeJKPK, Section 2.1] and [Reference Herschend and JørgensenHJ, Example 2.13].
$Q^{n,d}$
and relevant modules, see [Reference Jasso, Külshammer, Psaroudakis and KvammeJKPK, Section 2.1] and [Reference Herschend and JørgensenHJ, Example 2.13].
Next, we define the relation
on the set
![]() $\mathbb {Z}^{d+1}$
of all
$\mathbb {Z}^{d+1}$
of all
![]() $(d+1)$
-tuples over
$(d+1)$
-tuples over
![]() $\mathbb {Z}$
. Note that
$\mathbb {Z}$
. Note that
![]() $x\rightsquigarrow y$
implies
$x\rightsquigarrow y$
implies
![]() $x\leq y$
. Using the relation
$x\leq y$
. Using the relation
![]() $\rightsquigarrow $
, one can determine the
$\rightsquigarrow $
, one can determine the
![]() $\operatorname {Hom}$
-spaces between indecomposable modules in
$\operatorname {Hom}$
-spaces between indecomposable modules in
![]() $\mathcal {M}^d_{n}$
.
$\mathcal {M}^d_{n}$
.
Proposition 5.2 [Reference Oppermann and ThomasOT, Theorem 3.6(3)], [Reference Jasso, Külshammer, Psaroudakis and KvammeJKPK, Proposition 2.8].
Let
![]() $x,y\in \operatorname {os}_n^{d+1}$
. Then
$x,y\in \operatorname {os}_n^{d+1}$
. Then
 $$\begin{align*}\dim \operatorname{Hom}_{A_n^d}(M_x,M_y)=\begin{cases} 1 & \text{if } x\rightsquigarrow y \\ 0 &\text{otherwise}. \end{cases}\end{align*}$$
$$\begin{align*}\dim \operatorname{Hom}_{A_n^d}(M_x,M_y)=\begin{cases} 1 & \text{if } x\rightsquigarrow y \\ 0 &\text{otherwise}. \end{cases}\end{align*}$$
The d-extensions in
![]() $\mathcal {M}^d_{n}$
have a similar combinatorial description, including a description of all the middle terms. To this end, we define
$\mathcal {M}^d_{n}$
have a similar combinatorial description, including a description of all the middle terms. To this end, we define
![]() $\tau _d\colon \mathbb {Z}^{d+1}\to \mathbb {Z}^{d+1}$
by
$\tau _d\colon \mathbb {Z}^{d+1}\to \mathbb {Z}^{d+1}$
by
The notation is motivated by the fact that if
![]() $x\in \operatorname {os}_n^{d+1}$
with
$x\in \operatorname {os}_n^{d+1}$
with
![]() $x_0>0$
, then τ
d
(M
x
)≅M
τ
d
(x) by [Reference Jasso, Külshammer, Psaroudakis and KvammeJKPK, Proposition 2.7(iii)], where
$x_0>0$
, then τ
d
(M
x
)≅M
τ
d
(x) by [Reference Jasso, Külshammer, Psaroudakis and KvammeJKPK, Proposition 2.7(iii)], where
![]() $\tau _d (M_x)$
is the higher Auslander–Reiten translate of
$\tau _d (M_x)$
is the higher Auslander–Reiten translate of
![]() $M_x$
.
$M_x$
.
Proposition 5.3 [Reference Oppermann and ThomasOT, Theorem 3.6(4) and 3.8], [Reference Jasso, Külshammer, Psaroudakis and KvammeJKPK, Proposition 2.8].
Let
![]() $x,y\in \operatorname {os}_n^{d+1}$
. Then
$x,y\in \operatorname {os}_n^{d+1}$
. Then
 $$\begin{align*}\dim \operatorname{Ext}^{d}_{A_n^d}(M_y,M_x)= \begin{cases} 1 & \text{if } x \rightsquigarrow\tau_d(y) \\ 0 &\text{otherwise}. \end{cases}\end{align*}$$
$$\begin{align*}\dim \operatorname{Ext}^{d}_{A_n^d}(M_y,M_x)= \begin{cases} 1 & \text{if } x \rightsquigarrow\tau_d(y) \\ 0 &\text{otherwise}. \end{cases}\end{align*}$$
In particular, if
![]() $x\rightsquigarrow \tau _d(y)$
, there is a nontrivial d-extension
$x\rightsquigarrow \tau _d(y)$
, there is a nontrivial d-extension
where
![]() $E_k=\bigoplus _{z\in Z_k}M_z$
for
$E_k=\bigoplus _{z\in Z_k}M_z$
for
Remark 5.4. The d-extension (10) in Proposition 5.3 is minimal. This is seen by combining the fact that
![]() $E_k$
and
$E_k$
and
![]() $E_{k+1}$
have no isomorphic direct summands for
$E_{k+1}$
have no isomorphic direct summands for
![]() $k = 1,\dots ,d-1$
with Proposition 2.6 and Remark 2.7.
$k = 1,\dots ,d-1$
with Proposition 2.6 and Remark 2.7.
We will use the following lemma, which can be seen as an immediate consequence of the description of d-extensions in Proposition 5.3.
Lemma 5.5. Suppose that
![]() $x,y\in \operatorname {os}_n^{d+1}$
with
$x,y\in \operatorname {os}_n^{d+1}$
with
![]() $x_i=y_i$
for all
$x_i=y_i$
for all
![]() $i=0,\dots ,d-1$
and
$i=0,\dots ,d-1$
and
![]() $x_d \leq y_d$
. Then any nonzero morphism
$x_d \leq y_d$
. Then any nonzero morphism
![]() $M_{x} \to M_y$
is a monomorphism.
$M_{x} \to M_y$
is a monomorphism.
Proof. If
![]() $x_d=y_d$
, the only nonzero morphism (up to multiplication by a scalar) is the identity, which is a monomorphism. If
$x_d=y_d$
, the only nonzero morphism (up to multiplication by a scalar) is the identity, which is a monomorphism. If
![]() $x_d < y_d$
, the result follows from Proposition 5.3 when looking at the extension between
$x_d < y_d$
, the result follows from Proposition 5.3 when looking at the extension between
![]() $M_x$
and
$M_x$
and
![]() $M_z$
, where
$M_z$
, where
![]() $z=(x_1+1, \dots , x_d+1, y_d)$
.
$z=(x_1+1, \dots , x_d+1, y_d)$
.
Although Proposition 5.3 is limited to describing the middle terms in d-extensions with indecomposable end terms, we know from Theorem 3.20 that this knowledge is sufficient for producing d-torsion classes if we have already established closure under d-quotients.
5.2 A combinatorial characterisation of d-torsion classes in
 $\mathcal {M}^{d}_{n}$
.
$\mathcal {M}^{d}_{n}$
.
The main result of this subsection is a characterisation of higher torsion classes associated to higher Auslander algebras of type
![]() $\mathbb A$
; see Theorem 5.13. The key ingredient in the proof of this result is a combinatorial description of how to close a subcategory of
$\mathbb A$
; see Theorem 5.13. The key ingredient in the proof of this result is a combinatorial description of how to close a subcategory of
![]() $\mathcal {M}^d_{n}$
under d-quotients.
$\mathcal {M}^d_{n}$
under d-quotients.
Given
![]() $M \in \mathcal {M}^d_{n}$
, we write
$M \in \mathcal {M}^d_{n}$
, we write
![]() $\operatorname {dq}(M)$
for the smallest subcategory of
$\operatorname {dq}(M)$
for the smallest subcategory of
![]() $\mathcal {M}^d_{n}$
which contains M and is closed under d-quotients (see Definition 3.7). We often refer to
$\mathcal {M}^d_{n}$
which contains M and is closed under d-quotients (see Definition 3.7). We often refer to
![]() $\operatorname {dq}(M)$
as the d-quotient closure of M. It is clear that if
$\operatorname {dq}(M)$
as the d-quotient closure of M. It is clear that if
![]() $N \in \operatorname {dq}(M)$
, then
$N \in \operatorname {dq}(M)$
, then
![]() $\operatorname {dq}(N) \subseteq \operatorname {dq}(M)$
.
$\operatorname {dq}(N) \subseteq \operatorname {dq}(M)$
.
We filter
![]() $\operatorname {dq}(M)$
as follows:
$\operatorname {dq}(M)$
as follows:
-
○ Set
 $\operatorname {dq}(M)_0=\operatorname {add}(M)$
.
$\operatorname {dq}(M)_0=\operatorname {add}(M)$
. -
○ For
 $i \geq 0$
, set
$i \geq 0$
, set  $$\begin{align*}\operatorname{dq}(M)_{i+1} = \operatorname{add}\,\left\{ N \in \mathcal{M}^d_{n} \ \middle\vert \begin{array}{c} \exists \ \text{minimal}\ d\text{-}\text{quotient} \ X \to Y \to C_1 \to \dots \to C_d \to 0 \ \text{in} \\ \mathcal{M}^d_{n} \ \text{with} \ Y \in \operatorname{dq}(M)_i \ \text{and} \ N \cong C_j \ \text{for some}\ 1\leq j \leq d \end{array}\right\}. \end{align*}$$
$$\begin{align*}\operatorname{dq}(M)_{i+1} = \operatorname{add}\,\left\{ N \in \mathcal{M}^d_{n} \ \middle\vert \begin{array}{c} \exists \ \text{minimal}\ d\text{-}\text{quotient} \ X \to Y \to C_1 \to \dots \to C_d \to 0 \ \text{in} \\ \mathcal{M}^d_{n} \ \text{with} \ Y \in \operatorname{dq}(M)_i \ \text{and} \ N \cong C_j \ \text{for some}\ 1\leq j \leq d \end{array}\right\}. \end{align*}$$
We see that
![]() $\operatorname {dq}(M)_0 \subseteq \operatorname {dq}(M)_1 \subseteq \dots $
and that the chain must stabilise with
$\operatorname {dq}(M)_0 \subseteq \operatorname {dq}(M)_1 \subseteq \dots $
and that the chain must stabilise with
![]() $\operatorname {dq}(M)_t=\operatorname {dq}(M)_{t+1}$
for some
$\operatorname {dq}(M)_t=\operatorname {dq}(M)_{t+1}$
for some
![]() $t \in \mathbb {N}$
because
$t \in \mathbb {N}$
because
![]() $\mathcal {M}^d_{n}$
has finitely many indecomposables. By definition, we have
$\mathcal {M}^d_{n}$
has finitely many indecomposables. By definition, we have
![]() $\operatorname {dq}(M)=\operatorname {dq}(M)_t$
.
$\operatorname {dq}(M)=\operatorname {dq}(M)_t$
.
To completely determine the subcategory
![]() $\operatorname {dq}(M)$
, it is sufficient to describe the indecomposable modules it contains. With this in mind, we begin by identifying certain indecomposables which must be contained in d-quotient closures.
$\operatorname {dq}(M)$
, it is sufficient to describe the indecomposable modules it contains. With this in mind, we begin by identifying certain indecomposables which must be contained in d-quotient closures.
Lemma 5.6. Let
![]() $x \in \operatorname {os}_n^{d+1}$
be such that
$x \in \operatorname {os}_n^{d+1}$
be such that
![]() $x_i +1 \leq x_{i+1}$
for some
$x_i +1 \leq x_{i+1}$
for some
![]() $0\leq i \leq d-1$
and set
$0\leq i \leq d-1$
and set
![]() ${y=(x_0, \dots , x_{i-1}, x_i +1, x_{i+1}, \dots , x_d)}$
. Then
${y=(x_0, \dots , x_{i-1}, x_i +1, x_{i+1}, \dots , x_d)}$
. Then
![]() $M_{y} \in \operatorname {dq}(M_{x})$
.
$M_{y} \in \operatorname {dq}(M_{x})$
.
Proof. Define
![]() $z=(z_0, \dots , z_d)$
such that
$z=(z_0, \dots , z_d)$
such that
 $$\begin{align*}z_j = \begin{cases} x_j & \text{if } j \neq i+1 \\ x_i & \text{if } j=i+1. \end{cases} \end{align*}$$
$$\begin{align*}z_j = \begin{cases} x_j & \text{if } j \neq i+1 \\ x_i & \text{if } j=i+1. \end{cases} \end{align*}$$
We then have
![]() $z \rightsquigarrow x$
, so there is a nonzero morphism
$z \rightsquigarrow x$
, so there is a nonzero morphism
![]() $M_{z} \to M_x$
by Proposition 5.2. Because
$M_{z} \to M_x$
by Proposition 5.2. Because
![]() $x_i\leq z_{i+1}<x_{i+1}$
, the module
$x_i\leq z_{i+1}<x_{i+1}$
, the module
![]() $M_{y}$
is hence in
$M_{y}$
is hence in
![]() $\operatorname {dq}(M_{x})$
by [Reference Herschend and JørgensenHJ, Lemma 3.8(2)], keeping in mind that this paper uses a different notation as we outlined in Remark 5.1.
$\operatorname {dq}(M_{x})$
by [Reference Herschend and JørgensenHJ, Lemma 3.8(2)], keeping in mind that this paper uses a different notation as we outlined in Remark 5.1.
Lemma 5.6 yields the following corollary.
Corollary 5.7. Given any
![]() $x \in \operatorname {os}_n^{d+1}$
, the set
$x \in \operatorname {os}_n^{d+1}$
, the set
is contained in
![]() $\operatorname {dq}(M_{x})$
.
$\operatorname {dq}(M_{x})$
.
Proof. Suppose
![]() $y \in \operatorname {os}_n^{d+1}$
satisfies
$y \in \operatorname {os}_n^{d+1}$
satisfies
![]() $x \leq y$
and
$x \leq y$
and
![]() $x_d=y_d$
. Construct a sequence
$x_d=y_d$
. Construct a sequence
in
![]() $\operatorname {os}_n^{d+1}$
, where the element
$\operatorname {os}_n^{d+1}$
, where the element
![]() $z^{i+1}$
is constructed from
$z^{i+1}$
is constructed from
![]() $z^i$
as follows. If
$z^i$
as follows. If
![]() $z^i=y$
, then we are finished. Otherwise, there exists a maximal j such that
$z^i=y$
, then we are finished. Otherwise, there exists a maximal j such that
![]() $z_j^i < y_j$
, and we must have
$z_j^i < y_j$
, and we must have
![]() $j<d$
. Then
$j<d$
. Then
![]() $z_j^i+1 \leq y_j \leq y_{j+1}=z_{j+1}^i$
, and we define
$z_j^i+1 \leq y_j \leq y_{j+1}=z_{j+1}^i$
, and we define
 $$\begin{align*}z^{i+1}_k = \begin{cases} z^i_k+1 & \text{if } k=j \\ z^i_k & \text{if } k \neq j. \end{cases} \end{align*}$$
$$\begin{align*}z^{i+1}_k = \begin{cases} z^i_k+1 & \text{if } k=j \\ z^i_k & \text{if } k \neq j. \end{cases} \end{align*}$$
Notice that
![]() $M_{z^{i+1}} \in \operatorname {dq}(M_{z^i})$
by Lemma 5.6 and that this process must terminate with
$M_{z^{i+1}} \in \operatorname {dq}(M_{z^i})$
by Lemma 5.6 and that this process must terminate with
![]() $z^m=y$
. Thus, we get
$z^m=y$
. Thus, we get
as required.
We now present the key technical lemma needed to describe
![]() $\operatorname {dq}(M_x)$
completely.
$\operatorname {dq}(M_x)$
completely.
Lemma 5.8. Suppose that
![]() $C_0 \to C_1 \to \dots \to C_d \to 0$
is a minimal d-cokernel of a morphism
$C_0 \to C_1 \to \dots \to C_d \to 0$
is a minimal d-cokernel of a morphism
![]() $C_{-1} \rightarrow C_0$
in
$C_{-1} \rightarrow C_0$
in
![]() $\mathcal {M}^d_{n}$
. If
$\mathcal {M}^d_{n}$
. If
![]() $M_{z} \in \operatorname {add}(C_i)$
for some
$M_{z} \in \operatorname {add}(C_i)$
for some
![]() $1\leq i \leq d$
, then there exists
$1\leq i \leq d$
, then there exists
![]() $M_{x} \in \operatorname {add}(C_0)$
such that
$M_{x} \in \operatorname {add}(C_0)$
such that
![]() $x\leq z$
and
$x\leq z$
and
![]() $x_d=z_d$
.
$x_d=z_d$
.
Proof. Since each
![]() $C_i \in {\mathcal {M}}_n^d$
, we may assume that every
$C_i \in {\mathcal {M}}_n^d$
, we may assume that every
![]() $C_i$
is equal to a direct sum of modules of the form
$C_i$
is equal to a direct sum of modules of the form
![]() $M_z$
for
$M_z$
for
![]() $z\in \operatorname {os}_n^{d+1}$
. Choose
$z\in \operatorname {os}_n^{d+1}$
. Choose
![]() $M_{z} \in \operatorname {add}(C_i)$
. Write the morphism
$M_{z} \in \operatorname {add}(C_i)$
. Write the morphism
![]() $C_{i-1} \to C_i$
as
$C_{i-1} \to C_i$
as
 $$\begin{align*}\begin{pmatrix} f \\ g \end{pmatrix}\colon C_{i-1} \rightarrow M_{z} \oplus C_i'. \end{align*}$$
$$\begin{align*}\begin{pmatrix} f \\ g \end{pmatrix}\colon C_{i-1} \rightarrow M_{z} \oplus C_i'. \end{align*}$$
By the construction of minimal d-cokernels, this morphism factors through the cokernel K of the morphism
![]() $C_{i-2} \to C_{i-1}$
as indicated in the diagram
$C_{i-2} \to C_{i-1}$
as indicated in the diagram

where
![]() $\left (\begin {smallmatrix} f' \\ g' \end {smallmatrix}\right )$
is a minimal left
$\left (\begin {smallmatrix} f' \\ g' \end {smallmatrix}\right )$
is a minimal left
![]() $\mathcal {M}^d_{n}$
-approximation of K.
$\mathcal {M}^d_{n}$
-approximation of K.
There exists some
![]() $M_{w} \in \operatorname {add}(C_{i-1})$
with a nonzero morphism
$M_{w} \in \operatorname {add}(C_{i-1})$
with a nonzero morphism
![]() $M_{w} \to M_{z}$
. Indeed, if this is not the case, then
$M_{w} \to M_{z}$
. Indeed, if this is not the case, then
![]() $f=0$
. However, since
$f=0$
. However, since
![]() $\pi $
is an epimorphism, this would imply
$\pi $
is an epimorphism, this would imply
![]() $f'=0$
, contradicting
$f'=0$
, contradicting
![]() $\left (\begin {smallmatrix} f' \\ g' \end {smallmatrix}\right )$
being left minimal. Consequently, we may write
$\left (\begin {smallmatrix} f' \\ g' \end {smallmatrix}\right )$
being left minimal. Consequently, we may write
![]() $C_{i-1} = D \oplus D'$
, where
$C_{i-1} = D \oplus D'$
, where
![]() $D \neq 0$
and
$D \neq 0$
and
![]() $D'$
is the largest summand of
$D'$
is the largest summand of
![]() $C_{i-1}$
that maps to zero under f. This means that the morphism
$C_{i-1}$
that maps to zero under f. This means that the morphism
![]() $\left (\begin {smallmatrix} f \\ g \end {smallmatrix}\right )$
may be written as
$\left (\begin {smallmatrix} f \\ g \end {smallmatrix}\right )$
may be written as
 $$ \begin{align*} \begin{pmatrix} f_1 & 0 \\ g_1 & g_2 \end{pmatrix}\colon D \oplus D' \xrightarrow{} M_z \oplus C_i', \end{align*} $$
$$ \begin{align*} \begin{pmatrix} f_1 & 0 \\ g_1 & g_2 \end{pmatrix}\colon D \oplus D' \xrightarrow{} M_z \oplus C_i', \end{align*} $$
where
![]() $f_1$
is nonzero. For every
$f_1$
is nonzero. For every
![]() $M_{v} \in \operatorname {add}(D)$
, there is a nonzero morphism to
$M_{v} \in \operatorname {add}(D)$
, there is a nonzero morphism to
![]() $M_z$
. Hence, Proposition 5.2 shows that
$M_z$
. Hence, Proposition 5.2 shows that
![]() $v \rightsquigarrow z$
. Since
$v \rightsquigarrow z$
. Since
![]() $D \neq 0$
, we may choose
$D \neq 0$
, we may choose
![]() $M_y \in \operatorname {add}(D)$
with
$M_y \in \operatorname {add}(D)$
with
![]() $y_d$
maximal (i.e. for all
$y_d$
maximal (i.e. for all
![]() $M_{v} \in \operatorname {add}(D)$
, we have
$M_{v} \in \operatorname {add}(D)$
, we have
![]() $v_d \leq y_d).$
$v_d \leq y_d).$
With z and y fixed and knowing that
![]() $y \rightsquigarrow z$
, we may now consider
$y \rightsquigarrow z$
, we may now consider
![]() $z'=(z_0,z_1, \dots , z_{d-1},y_d)$
. Notice that
$z'=(z_0,z_1, \dots , z_{d-1},y_d)$
. Notice that
![]() $z' \rightsquigarrow z$
. Proposition 5.2 and Lemma 5.5 thus yield that there exists a monomorphism
$z' \rightsquigarrow z$
. Proposition 5.2 and Lemma 5.5 thus yield that there exists a monomorphism
![]() $\iota \colon M_{z'} \to M_z$
. Moreover, by the maximality of
$\iota \colon M_{z'} \to M_z$
. Moreover, by the maximality of
![]() $y_d$
, we have
$y_d$
, we have
![]() $v \rightsquigarrow z'$
for all
$v \rightsquigarrow z'$
for all
![]() $M_{v} \in \operatorname {add}(D)$
. Hence, by Proposition 5.2, there exists a morphism
$M_{v} \in \operatorname {add}(D)$
. Hence, by Proposition 5.2, there exists a morphism
![]() $h \colon D \rightarrow M_{z'}$
such that
$h \colon D \rightarrow M_{z'}$
such that
![]() $f_1 = \iota \circ h$
. In particular, the solid part of the diagram
$f_1 = \iota \circ h$
. In particular, the solid part of the diagram

commutes. Since
![]() $\left (\begin {smallmatrix} \iota & 0 \\ 0 & 1 \end {smallmatrix}\right )$
is a monomorphism, this implies that the composition of the morphism
$\left (\begin {smallmatrix} \iota & 0 \\ 0 & 1 \end {smallmatrix}\right )$
is a monomorphism, this implies that the composition of the morphism
![]() $C_{i-2} \to C_{i-1}$
and
$C_{i-2} \to C_{i-1}$
and
![]() $\left (\begin {smallmatrix} h & 0 \\ g_1 & g_2 \end {smallmatrix}\right )$
is zero. Thus, there is a morphism
$\left (\begin {smallmatrix} h & 0 \\ g_1 & g_2 \end {smallmatrix}\right )$
is zero. Thus, there is a morphism
![]() $t \colon K \to M_{z'} \oplus C_i'$
making the upper triangle in the diagram above commute.
$t \colon K \to M_{z'} \oplus C_i'$
making the upper triangle in the diagram above commute.
Note that the lower triangle also commutes as
![]() $\pi $
is an epimorphism. Finally, since
$\pi $
is an epimorphism. Finally, since
![]() $\left (\begin {smallmatrix} f' \\ g' \end {smallmatrix}\right )$
is an
$\left (\begin {smallmatrix} f' \\ g' \end {smallmatrix}\right )$
is an
![]() $\mathcal {M}^d_{n}$
-approximation, there exists a morphism
$\mathcal {M}^d_{n}$
-approximation, there exists a morphism
![]() $s \colon M_z \oplus C_i' \to M_{z'} \oplus C_i'$
such that
$s \colon M_z \oplus C_i' \to M_{z'} \oplus C_i'$
such that
 $$ \begin{align*} t=s \circ \begin{pmatrix} f' \\ g' \end{pmatrix}. \end{align*} $$
$$ \begin{align*} t=s \circ \begin{pmatrix} f' \\ g' \end{pmatrix}. \end{align*} $$
It follows that
 $$ \begin{align*} \begin{pmatrix} f' \\ g' \end{pmatrix} = \begin{pmatrix} \iota & 0 \\ 0 & 1 \end{pmatrix} \circ t = \begin{pmatrix} \iota & 0 \\ 0 & 1 \end{pmatrix} \circ s \circ \begin{pmatrix} f' \\ g' \end{pmatrix}, \end{align*} $$
$$ \begin{align*} \begin{pmatrix} f' \\ g' \end{pmatrix} = \begin{pmatrix} \iota & 0 \\ 0 & 1 \end{pmatrix} \circ t = \begin{pmatrix} \iota & 0 \\ 0 & 1 \end{pmatrix} \circ s \circ \begin{pmatrix} f' \\ g' \end{pmatrix}, \end{align*} $$
and thus,
![]() $\left (\begin {smallmatrix} \iota & 0 \\ 0 & 1 \end {smallmatrix}\right ) \circ s$
is an isomorphism, since
$\left (\begin {smallmatrix} \iota & 0 \\ 0 & 1 \end {smallmatrix}\right ) \circ s$
is an isomorphism, since
![]() $\left (\begin {smallmatrix} f' \\ g' \end {smallmatrix}\right )$
is left minimal. Therefore, the monomorphism
$\left (\begin {smallmatrix} f' \\ g' \end {smallmatrix}\right )$
is left minimal. Therefore, the monomorphism
![]() $\iota $
is also an epimorphism, so it must be an isomorphism, and we have
$\iota $
is also an epimorphism, so it must be an isomorphism, and we have
![]() $M_{z}\cong M_{z'}$
. This shows that
$M_{z}\cong M_{z'}$
. This shows that
![]() $y_d=z_d$
, and hence,
$y_d=z_d$
, and hence,
![]() $M_y \in \operatorname {add}(C_{i-1})$
satisfies both
$M_y \in \operatorname {add}(C_{i-1})$
satisfies both
![]() $y \rightsquigarrow z$
(and thus,
$y \rightsquigarrow z$
(and thus,
![]() $y \leq z$
) and
$y \leq z$
) and
![]() $y_d=z_d$
.
$y_d=z_d$
.
We can now repeat the argument with
![]() $M_y$
and keep going until we get
$M_y$
and keep going until we get
![]() $M_{x} \in \operatorname {add}(C_0)$
with
$M_{x} \in \operatorname {add}(C_0)$
with
![]() $x\leq y\leq z$
and
$x\leq y\leq z$
and
![]() $x_d=y_d=z_d$
.
$x_d=y_d=z_d$
.
Lemma 5.8 enables us to fully describe
![]() $\operatorname {dq}(M_x)$
for an indecomposable module
$\operatorname {dq}(M_x)$
for an indecomposable module
![]() $M_x \in \mathcal {M}^d_{n}$
.
$M_x \in \mathcal {M}^d_{n}$
.
Corollary 5.9. Given any
![]() $x \in \operatorname {os}_n^{d+1}$
, we have
$x \in \operatorname {os}_n^{d+1}$
, we have
Proof. By Corollary 5.7, it suffices to show that for any
![]() $M_y \in \operatorname {dq}(M_x)$
, we must have
$M_y \in \operatorname {dq}(M_x)$
, we must have
![]() $x \leq y$
and
$x \leq y$
and
![]() $x_d=y_d$
. Let
$x_d=y_d$
. Let
![]() $i\geq 0$
be such that
$i\geq 0$
be such that
![]() $M_y \in \operatorname {dq}(M_x)_i$
. If
$M_y \in \operatorname {dq}(M_x)_i$
. If
![]() $i=0$
, we have
$i=0$
, we have
![]() $M_y \in \operatorname {dq}(M_x)_0 = \operatorname {add}(M_x)$
, so
$M_y \in \operatorname {dq}(M_x)_0 = \operatorname {add}(M_x)$
, so
![]() $M_y = M_x$
, and the statement holds. Assume hence,
$M_y = M_x$
, and the statement holds. Assume hence,
![]() $i>0$
. By Lemma 5.8, there exists
$i>0$
. By Lemma 5.8, there exists
![]() $M_z \in \operatorname {dq}(M_x)_{i-1}$
such that
$M_z \in \operatorname {dq}(M_x)_{i-1}$
such that
![]() $z \leq y$
and
$z \leq y$
and
![]() $z_d=y_d$
.
$z_d=y_d$
.
Repeating this argument, we will eventually find some
![]() $M_w \in \operatorname {dq}(M_x)_0$
such that
$M_w \in \operatorname {dq}(M_x)_0$
such that
![]() $w\leq y$
and
$w\leq y$
and
![]() $w_d=y_d$
. As
$w_d=y_d$
. As
![]() $\operatorname {dq}(M_x)_0=\operatorname {add}(M_x)$
yields
$\operatorname {dq}(M_x)_0=\operatorname {add}(M_x)$
yields
![]() $M_w=M_x$
, the result follows.
$M_w=M_x$
, the result follows.
Remark 5.10. It follows from Corollary 5.9 that any
![]() $M_y, M_z \in \operatorname {dq}(M_x)$
satisfy
$M_y, M_z \in \operatorname {dq}(M_x)$
satisfy
![]() $y_d =x_d=z_d$
, and thus there are no nontrivial d-extensions between them by Proposition 5.3. In particular, the subcategory
$y_d =x_d=z_d$
, and thus there are no nontrivial d-extensions between them by Proposition 5.3. In particular, the subcategory
![]() $\operatorname {dq}(M_x)$
is closed under d-extensions, and it is hence the smallest d-torsion class containing
$\operatorname {dq}(M_x)$
is closed under d-extensions, and it is hence the smallest d-torsion class containing
![]() $M_x$
by Theorem 3.17.
$M_x$
by Theorem 3.17.
We now consider the d-quotient closure of a set of indecomposables.
Proposition 5.11. Given any subset
![]() $I \subseteq \operatorname {os}_n^{d+1}$
, suppose that
$I \subseteq \operatorname {os}_n^{d+1}$
, suppose that
![]() $M_y \in \operatorname {dq}\left (\bigoplus _{x \in I} M_x\right )$
. Then
$M_y \in \operatorname {dq}\left (\bigoplus _{x \in I} M_x\right )$
. Then
![]() $M_y \in \operatorname {dq}(M_x)$
for some
$M_y \in \operatorname {dq}(M_x)$
for some
![]() $x \in I$
.
$x \in I$
.
Proof. We prove this by induction on the filtration of
![]() $\operatorname {dq}(\bigoplus _{x \in I} M_x)$
. If
$\operatorname {dq}(\bigoplus _{x \in I} M_x)$
. If
 $$\begin{align*}M_y \in \operatorname{dq}\,\left(\bigoplus_{x \in I} M_x\right)_{0}=\operatorname{add}\,\left(\bigoplus_{x \in I} M_x\right), \end{align*}$$
$$\begin{align*}M_y \in \operatorname{dq}\,\left(\bigoplus_{x \in I} M_x\right)_{0}=\operatorname{add}\,\left(\bigoplus_{x \in I} M_x\right), \end{align*}$$
the statement clearly holds.
Now suppose
![]() $M_y \in \operatorname {dq}\left (\bigoplus _{x \in I} M_x\right )_i$
for some
$M_y \in \operatorname {dq}\left (\bigoplus _{x \in I} M_x\right )_i$
for some
![]() $i>0$
and that the result is known for all
$i>0$
and that the result is known for all
![]() $M_z \in \operatorname {dq}\left (\bigoplus _{x \in I} M_x\right )_{i-1}$
. By construction, there must exist a minimal d-quotient
$M_z \in \operatorname {dq}\left (\bigoplus _{x \in I} M_x\right )_{i-1}$
. By construction, there must exist a minimal d-quotient
in
![]() $\mathcal {M}^d_{n}$
of some morphism f such that
$\mathcal {M}^d_{n}$
of some morphism f such that
![]() $Y \in \operatorname {dq}\left (\bigoplus _{x \in I} M_x\right )_{i-1}$
and
$Y \in \operatorname {dq}\left (\bigoplus _{x \in I} M_x\right )_{i-1}$
and
![]() $M_y \in \operatorname {add}(C_j)$
for some
$M_y \in \operatorname {add}(C_j)$
for some
![]() $1\leq j \leq d$
. Hence, combining Lemma 5.8 with Corollary 5.7 shows that there exists
$1\leq j \leq d$
. Hence, combining Lemma 5.8 with Corollary 5.7 shows that there exists
 $$\begin{align*}M_z \in \operatorname{add}(Y) \subseteq \operatorname{dq}\,\left(\bigoplus_{x \in I} M_x\right)_{i-1} \end{align*}$$
$$\begin{align*}M_z \in \operatorname{add}(Y) \subseteq \operatorname{dq}\,\left(\bigoplus_{x \in I} M_x\right)_{i-1} \end{align*}$$
such that
![]() $M_y \in \operatorname {dq}(M_z)$
. By the induction hypothesis, we have
$M_y \in \operatorname {dq}(M_z)$
. By the induction hypothesis, we have
![]() $M_z \in \operatorname {dq}(M_x)$
for some
$M_z \in \operatorname {dq}(M_x)$
for some
![]() $x \in I$
, and thus, it follows that
$x \in I$
, and thus, it follows that
![]() $M_y \in \operatorname {dq}(M_z) \subseteq \operatorname {dq}(M_x)$
, as required.
$M_y \in \operatorname {dq}(M_z) \subseteq \operatorname {dq}(M_x)$
, as required.
Using Proposition 5.11, we are able to give a complete description of the d-quotient closure of any module in
![]() $\mathcal {M}^d_{n}$
.
$\mathcal {M}^d_{n}$
.
Corollary 5.12. Given a subset
![]() $I \subseteq \operatorname {os}_n^{d+1}$
, the set of indecomposable modules in
$I \subseteq \operatorname {os}_n^{d+1}$
, the set of indecomposable modules in
![]() $\operatorname {dq}\left (\bigoplus _{x \in I} M_x\right )$
is precisely
$\operatorname {dq}\left (\bigoplus _{x \in I} M_x\right )$
is precisely
Proof. Since it is clear that
![]() $\operatorname {dq}(M_x) \subseteq \operatorname {dq}\left (\bigoplus _{x \in I} M_x\right )$
for each
$\operatorname {dq}(M_x) \subseteq \operatorname {dq}\left (\bigoplus _{x \in I} M_x\right )$
for each
![]() $x \in I$
, this is a direct consequence of Corollary 5.9 and Proposition 5.11.
$x \in I$
, this is a direct consequence of Corollary 5.9 and Proposition 5.11.
For a set of indecomposable modules in
![]() $\mathcal {M}^d_{n}$
, Corollary 5.12 gives a purely combinatorial description of all the indecomposables in their d-quotient closure. Unlike what we saw in Remark 5.10, there may now exist nontrivial d-extensions, so the d-quotient closure is not necessarily a d-torsion class. However, using the results developed in this subsection, we give a full combinatorial description of the subsets corresponding to d-torsion classes. Note that any subcategory of
$\mathcal {M}^d_{n}$
, Corollary 5.12 gives a purely combinatorial description of all the indecomposables in their d-quotient closure. Unlike what we saw in Remark 5.10, there may now exist nontrivial d-extensions, so the d-quotient closure is not necessarily a d-torsion class. However, using the results developed in this subsection, we give a full combinatorial description of the subsets corresponding to d-torsion classes. Note that any subcategory of
![]() $\mathcal {M}^d_{n}$
which is closed under direct summands is uniquely determined by its indecomposable modules (i.e., by a subset of
$\mathcal {M}^d_{n}$
which is closed under direct summands is uniquely determined by its indecomposable modules (i.e., by a subset of
![]() $\operatorname {os}_n^{d+1}$
). We hence use the notation
$\operatorname {os}_n^{d+1}$
). We hence use the notation
for the subcategory of
![]() $\mathcal {M}^d_{n}$
associated to a subset
$\mathcal {M}^d_{n}$
associated to a subset
![]() $I \subseteq \operatorname {os}_n^{d+1}$
.
$I \subseteq \operatorname {os}_n^{d+1}$
.
Theorem 5.13. Consider a subset
![]() $I \subseteq \operatorname {os}_n^{d+1}$
. The subcategory
$I \subseteq \operatorname {os}_n^{d+1}$
. The subcategory
![]() $\mathcal {U}_I$
is a d-torsion class in
$\mathcal {U}_I$
is a d-torsion class in
![]() $\mathcal {M}^d_{n}$
if and only if the following hold for any elements
$\mathcal {M}^d_{n}$
if and only if the following hold for any elements
![]() $x,z\in \operatorname {os}_n^{d+1}$
:
$x,z\in \operatorname {os}_n^{d+1}$
:
-
(1) If
 $x\leq z$
and
$x\leq z$
and
 $x_d=z_d$
, then
$x_d=z_d$
, then
 $x\in I$
implies
$x\in I$
implies
 $z\in I$
.
$z\in I$
. -
(2) If
 $x\rightsquigarrow \tau _d(z)$
and
$x\rightsquigarrow \tau _d(z)$
and
 $x,z\in I$
, then any
$x,z\in I$
, then any
 $y\in \operatorname {os}_n^{d+1}$
with
$y\in \operatorname {os}_n^{d+1}$
with
 $y_i \in \{x_i,z_i\}$
for each i must be in I.
$y_i \in \{x_i,z_i\}$
for each i must be in I.
Remark 5.14. The product order on
![]() $N_n^{d+1}$
restricts to a partial order on the subset
$N_n^{d+1}$
restricts to a partial order on the subset
Theorem 5.13(1) is equivalent to
![]() $\{y\in I\mid y_d=m\}$
being an upper set in
$\{y\in I\mid y_d=m\}$
being an upper set in
![]() $\{y\in \operatorname {os}_n^{d+1} \mid y_d=m\}$
for each
$\{y\in \operatorname {os}_n^{d+1} \mid y_d=m\}$
for each
![]() $m= 0,\ldots , n-1$
.
$m= 0,\ldots , n-1$
.
Proof of Theorem 5.13.
By Corollary 5.12, condition (1) holds if and only if
![]() $\mathcal {U}_I$
is closed under d-quotients. It follows from Proposition 5.3 and Remark 5.4 that condition (2) is equivalent to
$\mathcal {U}_I$
is closed under d-quotients. It follows from Proposition 5.3 and Remark 5.4 that condition (2) is equivalent to
![]() $\mathcal {U}_I$
being closed under d-extensions by indecomposables. Moreover, if
$\mathcal {U}_I$
being closed under d-extensions by indecomposables. Moreover, if
![]() $\mathcal {U}_I$
is closed under d-quotients, it is closed under d-extensions by indecomposables if and only if it is closed under all d-extensions by Theorem 3.20. From Theorem 3.17, we know that
$\mathcal {U}_I$
is closed under d-quotients, it is closed under d-extensions by indecomposables if and only if it is closed under all d-extensions by Theorem 3.20. From Theorem 3.17, we know that
![]() $\mathcal {U}_I$
is a d-torsion class if and only if it is closed under d-extensions and d-quotients, which proves the claim.
$\mathcal {U}_I$
is a d-torsion class if and only if it is closed under d-extensions and d-quotients, which proves the claim.
5.3 Computational results
We are now ready to present two algorithms for explicitly computing higher torsion classes associated to higher Auslander algebras of type
![]() $\mathbb A$
. The first algorithm computes the minimal d-torsion class containing a given module. The second computes all d-torsion classes associated to a higher Auslander algebra. Python code implementing the algorithms is available as a Google Colab notebook.Footnote 1
$\mathbb A$
. The first algorithm computes the minimal d-torsion class containing a given module. The second computes all d-torsion classes associated to a higher Auslander algebra. Python code implementing the algorithms is available as a Google Colab notebook.Footnote 1
We extend our notation for the sake of readability. In particular, for an element
![]() $x\in \operatorname {os}_n^{d+1}$
, we set
$x\in \operatorname {os}_n^{d+1}$
, we set
![]() $\operatorname {dq}(x)=\{y \in \operatorname {os}_n^{d+1} \mid M_y\in \operatorname {dq}(M_x)\}$
. By Corollary 5.9, we know that
$\operatorname {dq}(x)=\{y \in \operatorname {os}_n^{d+1} \mid M_y\in \operatorname {dq}(M_x)\}$
. By Corollary 5.9, we know that
Given a set of indecomposable modules
![]() $M_{x^1}, \dots , M_{x^r}$
in
$M_{x^1}, \dots , M_{x^r}$
in
![]() $\mathcal {M}^d_{n}$
, we let
$\mathcal {M}^d_{n}$
, we let
![]() $\mathcal {U}(M_{x^1}, \dots , M_{x^r})$
denote the smallest d-torsion class in
$\mathcal {U}(M_{x^1}, \dots , M_{x^r})$
denote the smallest d-torsion class in
![]() $\mathcal {M}^d_{n}$
containing
$\mathcal {M}^d_{n}$
containing
![]() $M_{x^1}, \dots , M_{x^r}$
. For a set
$M_{x^1}, \dots , M_{x^r}$
. For a set
![]() $X = \{x^1, \dots , x^r\} \subseteq \operatorname {os}_n^{d+1}$
, we let
$X = \{x^1, \dots , x^r\} \subseteq \operatorname {os}_n^{d+1}$
, we let
![]() $U(X)$
be the set of
$U(X)$
be the set of
![]() $(d+1)$
-tuples in
$(d+1)$
-tuples in
![]() $\operatorname {os}^{d+1}_n$
corresponding to the indecomposables in
$\operatorname {os}^{d+1}_n$
corresponding to the indecomposables in
![]() $\mathcal {U}(M_{x^1}, \dots , M_{x^r})$
. If the set X is empty, then
$\mathcal {U}(M_{x^1}, \dots , M_{x^r})$
. If the set X is empty, then
![]() $U(X)$
is also empty and corresponds to the trivial d-torsion class
$U(X)$
is also empty and corresponds to the trivial d-torsion class
![]() $\{0\}$
.
$\{0\}$
.
Algorithm 5.15. Given a set of initial indecomposable modules in
![]() $\mathcal {M}^d_{n}$
, or equivalently, a subset of
$\mathcal {M}^d_{n}$
, or equivalently, a subset of
![]() $\operatorname {os}^{d+1}_n$
, this algorithm computes the minimal d-torsion class containing those modules.
$\operatorname {os}^{d+1}_n$
, this algorithm computes the minimal d-torsion class containing those modules.
Input: Integers d ≥ 1, n ≥ 1 and a set X = {x 1, …, x
r
}⊆
![]() $\operatorname {os}^{d+1}_n$
.
$\operatorname {os}^{d+1}_n$
.
-
(1) Let I = X.
-
(2) For each pair x, y ∈ I such that x ⇝ τ d (y), add the (d + 1)-tuple (x 0, …, x d−1, y d ) to I.
-
(3) For every x ∈ I, add the elements of dq(x) to I.
-
(4) If new elements were added to I in step (2) or (3), repeat from step (2). Otherwise, terminate the process.
Output: The set I.
Since
![]() $\operatorname {os}_n^{d+1}$
is a finite set, Algorithm 5.15 will always terminate and give a subset
$\operatorname {os}_n^{d+1}$
is a finite set, Algorithm 5.15 will always terminate and give a subset
![]() $I \subseteq \operatorname {os}_n^{d+1}$
as output. Recall that we use the notation
$I \subseteq \operatorname {os}_n^{d+1}$
as output. Recall that we use the notation
for the corresponding subcategory of
![]() $\mathcal {M}^d_{n}$
. Proposition 5.16 shows that the set I produced in Algorithm 5.15 indeed corresponds to the minimal d-torsion class containing the indecomposable modules we started with.
$\mathcal {M}^d_{n}$
. Proposition 5.16 shows that the set I produced in Algorithm 5.15 indeed corresponds to the minimal d-torsion class containing the indecomposable modules we started with.
Proposition 5.16. The set I constructed in Algorithm 5.15 satisfies
![]() $\mathcal {U}_I=\mathcal {U}(M_{x^1}, \dots , M_{x^r})$
.
$\mathcal {U}_I=\mathcal {U}(M_{x^1}, \dots , M_{x^r})$
.
Proof. We need to show that
![]() $\mathcal {U}_I$
is the minimal d-torsion class containing
$\mathcal {U}_I$
is the minimal d-torsion class containing
![]() $M_{x^1}, \dots , M_{x^r}$
. Step (1) of the algorithm ensures that
$M_{x^1}, \dots , M_{x^r}$
. Step (1) of the algorithm ensures that
![]() $M_{x^1}, \dots , M_{x^r}\in \mathcal {U}_I$
. By Proposition 5.11, step (3) implies that
$M_{x^1}, \dots , M_{x^r}\in \mathcal {U}_I$
. By Proposition 5.11, step (3) implies that
![]() $\mathcal {U}_I$
is closed under d-quotients.
$\mathcal {U}_I$
is closed under d-quotients.
Consider two indecomposable modules
![]() $M_x, M_y \in \mathcal {U}_I$
with
$M_x, M_y \in \mathcal {U}_I$
with
![]() $\operatorname {Ext}^d_{A_n^d}(M_y,M_x) \neq 0$
. This means that the pair
$\operatorname {Ext}^d_{A_n^d}(M_y,M_x) \neq 0$
. This means that the pair
![]() $x,y \in I$
satisfies
$x,y \in I$
satisfies
![]() $x\rightsquigarrow \tau _d(y)$
by Proposition 5.3. Moreover, if
$x\rightsquigarrow \tau _d(y)$
by Proposition 5.3. Moreover, if
![]() $M_z$
is a direct summand in one of the middle terms in the nontrivial d-extension from
$M_z$
is a direct summand in one of the middle terms in the nontrivial d-extension from
![]() $M_x$
to
$M_x$
to
![]() $M_y$
described in Proposition 5.3, then either
$M_y$
described in Proposition 5.3, then either
![]() $z\in \operatorname {dq}(x)$
or
$z\in \operatorname {dq}(x)$
or
![]() $z\in \operatorname {dq}((x_{0}, \dots ,x_{d-1}, y_d))$
. Step (2) followed by step (3) thus ensures that
$z\in \operatorname {dq}((x_{0}, \dots ,x_{d-1}, y_d))$
. Step (2) followed by step (3) thus ensures that
![]() $M_z \in \mathcal {U}_I$
, so
$M_z \in \mathcal {U}_I$
, so
![]() $\mathcal {U}_I$
is closed under d-extensions with indecomposable end terms. By Theorem 3.20, this implies that
$\mathcal {U}_I$
is closed under d-extensions with indecomposable end terms. By Theorem 3.20, this implies that
![]() $\mathcal {U}_I$
is closed under all d-extensions. We can hence conclude that
$\mathcal {U}_I$
is closed under all d-extensions. We can hence conclude that
![]() $\mathcal {U}_I$
is a d-torsion class by Theorem 3.17.
$\mathcal {U}_I$
is a d-torsion class by Theorem 3.17.
We now know that
![]() $\mathcal {U}_I$
is a d-torsion class containing the modules
$\mathcal {U}_I$
is a d-torsion class containing the modules
![]() $M_{x^1}, \dots , M_{x^r}$
. However, objects added to I in the algorithm correspond to either
$M_{x^1}, \dots , M_{x^r}$
. However, objects added to I in the algorithm correspond to either
![]() $M_{x^1}, \dots , M_{x^r}$
or to indecomposable direct summands obtained from minimal d-quotients or minimal d-extensions – see Remark 5.4 – and the result follows.
$M_{x^1}, \dots , M_{x^r}$
or to indecomposable direct summands obtained from minimal d-quotients or minimal d-extensions – see Remark 5.4 – and the result follows.
Remark 5.17. An improvement of Algorithm 5.15, omitted for the sake of readability, is that on subsequent iterations it suffices to only consider
![]() $(d+1)$
-tuples added in the previous iteration in step (3). Similarly, in step (2), one only needs to consider pairs where at least one
$(d+1)$
-tuples added in the previous iteration in step (3). Similarly, in step (2), one only needs to consider pairs where at least one
![]() $(d+1)$
-tuple was added in the previous iteration.
$(d+1)$
-tuple was added in the previous iteration.
Building on Algorithm 5.15, we give an algorithm that determines all d-torsion classes in
![]() ${\mathcal {M}}_n^d$
.
${\mathcal {M}}_n^d$
.
Algorithm 5.18. This algorithm computes all higher torsion classes associated to a higher Auslander algebra.
Input: Integers d ≥ 1, n ≥ 1.
-
(1) Let 𝔘 be the singleton set containing the empty set. Set l = 1.
-
(2) For all sets X consisting of l distinct (d + 1)-tuples in
 $\operatorname {os}^{d+1}_n$
, compute U(X) using Algorithm 5.15 and add it to 𝔘.
$\operatorname {os}^{d+1}_n$
, compute U(X) using Algorithm 5.15 and add it to 𝔘. -
(3) If new elements were added to 𝔘 in step (2), increase l by one and repeat from step (2). Otherwise, terminate the process.
Output: The set 𝔘.
Similarly as in the case of Algorithm 5.15, it should be noted that the algorithm above must terminate as
![]() $\operatorname {os}_n^{d+1}$
is a finite set.
$\operatorname {os}_n^{d+1}$
is a finite set.
Proposition 5.19. The d-torsion classes in
![]() $\mathcal {M}^d_{n}$
are indexed by
$\mathcal {M}^d_{n}$
are indexed by
![]() $\mathfrak {U}$
. In other words,
$\mathfrak {U}$
. In other words,
Proof. First, observe that the trivial d-torsion class
![]() $\{0\}=\mathcal {U}_{\emptyset }$
, and
$\{0\}=\mathcal {U}_{\emptyset }$
, and
![]() $\emptyset \in \mathfrak {U}$
. As
$\emptyset \in \mathfrak {U}$
. As
![]() ${\mathcal {M}}_n^d$
has finitely many indecomposable objects, any nontrivial d-torsion class
${\mathcal {M}}_n^d$
has finitely many indecomposable objects, any nontrivial d-torsion class
![]() $\mathcal {V}$
in
$\mathcal {V}$
in
![]() ${\mathcal {M}}_n^d$
can be written as
${\mathcal {M}}_n^d$
can be written as
![]() $\mathcal {V}=\mathcal {U}(M_{x^1}, \dots , M_{x^m})$
for some positive integer m.
$\mathcal {V}=\mathcal {U}(M_{x^1}, \dots , M_{x^m})$
for some positive integer m.
Let r be the lowest positive integer for which any d-torsion class of the form
![]() $\mathcal {U}(M_{x^1}, \dots , M_{x^r})$
can also be written as
$\mathcal {U}(M_{x^1}, \dots , M_{x^r})$
can also be written as
![]() $\mathcal {U}(M_{y^1}, \dots , M_{y^s})$
for some
$\mathcal {U}(M_{y^1}, \dots , M_{y^s})$
for some
![]() $s<r$
. By construction, the set
$s<r$
. By construction, the set
![]() $\mathfrak {U}$
indexes all d-torsion classes of the form
$\mathfrak {U}$
indexes all d-torsion classes of the form
![]() $\mathcal {U}(M_{x^1}, \dots , M_{x^l})$
for
$\mathcal {U}(M_{x^1}, \dots , M_{x^l})$
for
![]() $l<r$
.
$l<r$
.
Suppose that
![]() $\mathcal {V}$
is a nontrivial d-torsion class, and let
$\mathcal {V}$
is a nontrivial d-torsion class, and let
![]() $m\geq 0$
be minimal such that
$m\geq 0$
be minimal such that
We claim that
![]() $\mathcal {V}=\mathcal {U}_I$
for some
$\mathcal {V}=\mathcal {U}_I$
for some
![]() $I\in \mathfrak {U}$
(i.e., that
$I\in \mathfrak {U}$
(i.e., that
![]() $m<r$
). Indeed, if
$m<r$
). Indeed, if
![]() $m\geq r$
, consider the d-torsion class
$m\geq r$
, consider the d-torsion class
![]() $\mathcal {V}'= \mathcal {U}(M_{x^1}, \dots , M_{x^{r}})$
. By the assumption on r, we can write
$\mathcal {V}'= \mathcal {U}(M_{x^1}, \dots , M_{x^{r}})$
. By the assumption on r, we can write
![]() $\mathcal {V}'$
as
$\mathcal {V}'$
as
![]() $\mathcal {U}(M_{z^1}, \dots , M_{z^s})$
for some
$\mathcal {U}(M_{z^1}, \dots , M_{z^s})$
for some
![]() $s< r$
. But then
$s< r$
. But then
![]() $\mathcal {V}$
is of the form
$\mathcal {V}$
is of the form
![]() $\mathcal {U}(M_{z^1}, \dots M_{z^s},M_{x^{r+1}},\dots M_{x^m})$
and can hence be generated by
$\mathcal {U}(M_{z^1}, \dots M_{z^s},M_{x^{r+1}},\dots M_{x^m})$
and can hence be generated by
![]() $m+s-r<m$
indecomposable modules. This contradicts the minimality of m, and the result follows.
$m+s-r<m$
indecomposable modules. This contradicts the minimality of m, and the result follows.
Remark 5.20. As before, Algorithm 5.18 is presented in its simplest form for the sake of readability. For efficient computations, we use the following improvements:
-
○ We precalculate whether
 $x \rightsquigarrow y$
and
$x \rightsquigarrow y$
and
 $x \rightsquigarrow \tau _d(y)$
for all
$x \rightsquigarrow \tau _d(y)$
for all
 $x,y \in \operatorname {os}_n^{d+1}$
.
$x,y \in \operatorname {os}_n^{d+1}$
. -
○ If a set X contains
 $x,y$
with
$x,y$
with
 $y\in \operatorname {dq}(x)$
, then
$y\in \operatorname {dq}(x)$
, then
 $U(X)$
has already been added to
$U(X)$
has already been added to
 $\mathfrak {U}$
, so we skip the computation of
$\mathfrak {U}$
, so we skip the computation of
 $U(X)$
in step (2).
$U(X)$
in step (2).
Using Algorithm 5.18, we can compute the number of higher torsion classes associated to a higher Auslander algebra. These computational results are summarised in Table 2.
Table 2 The number of d-torsion classes in the d-cluster tilting subcategory
![]() $\mathcal {M}^d_{n}$
of the higher Auslander algebra
$\mathcal {M}^d_{n}$
of the higher Auslander algebra
![]() $A_{n}^d$
.
$A_{n}^d$
.

In addition to computing the full set of d-torsion classes in
![]() ${\mathcal {M}}_n^d$
, our code also produces the associated Hasse diagram. Note that it gives a fully annotated version of the Hasse diagram, specifying the indecomposable modules contained in each d-torsion class.
${\mathcal {M}}_n^d$
, our code also produces the associated Hasse diagram. Note that it gives a fully annotated version of the Hasse diagram, specifying the indecomposable modules contained in each d-torsion class.
Example 5.21. Consider the higher Auslander algebra
![]() $A_{3}^{3}$
. The Hasse diagram of the
$A_{3}^{3}$
. The Hasse diagram of the
![]() $3$
-torsion classes in the
$3$
-torsion classes in the
![]() $3$
-cluster tilting subcategory
$3$
-cluster tilting subcategory
![]() ${\mathcal {M}}_3^3$
is shown in Figure 3. We note that the vertices labelled w, x and v have valency
${\mathcal {M}}_3^3$
is shown in Figure 3. We note that the vertices labelled w, x and v have valency
![]() $3$
,
$3$
,
![]() $4$
and
$4$
and
![]() $5$
, respectively, so the lattice is not Hasse-regular. We moreover note that the lattice is not semi-distributive as it fails the criterion of meet-semi-distributivity [Reference GrätzerG, p. 479]. Indeed, using the notation
$5$
, respectively, so the lattice is not Hasse-regular. We moreover note that the lattice is not semi-distributive as it fails the criterion of meet-semi-distributivity [Reference GrätzerG, p. 479]. Indeed, using the notation
![]() $\vee $
for join and
$\vee $
for join and
![]() $\wedge $
for meet, we see that
$\wedge $
for meet, we see that
![]() $x\wedge y=v=x\wedge z$
, but that
$x\wedge y=v=x\wedge z$
, but that
![]() $x \wedge (y\vee z)=x \wedge w =x \neq v$
.
$x \wedge (y\vee z)=x \wedge w =x \neq v$
.

Figure 3 The Hasse diagram of the
![]() $3$
-torsion classes in the
$3$
-torsion classes in the
![]() $3$
-cluster tilting subcategory
$3$
-cluster tilting subcategory
![]() ${\mathcal {M}}_3^3$
of the higher Auslander Algebra
${\mathcal {M}}_3^3$
of the higher Auslander Algebra
![]() $A_{3}^{3}$
.
$A_{3}^{3}$
.
6 Higher Nakayama algebras
Higher Nakayama algebras were introduced in [Reference Jasso, Külshammer, Psaroudakis and KvammeJKPK] as a higher-dimensional generalisation of classical Nakayama algebras. In this section, we extend the combinatorial description of higher torsion classes from Theorem 5.13 to the setup of higher Nakayama algebras. We first consider higher Nakayama algebras of type
![]() $\mathbb {A}$
in Section 6.1, before moving on to type
$\mathbb {A}$
in Section 6.1, before moving on to type
![]() $\mathbb {A}_\infty ^\infty $
in Section 6.2.
$\mathbb {A}_\infty ^\infty $
in Section 6.2.
6.1 Higher Nakayama algebras of type
 $\mathbb {A}$
$\mathbb {A}$
We start by giving a brief introduction to the construction of higher Nakayama algebras of type
![]() $\mathbb {A}$
. Let n and d be positive integers, and recall the definitions of
$\mathbb {A}$
. Let n and d be positive integers, and recall the definitions of
![]() $\operatorname {os}_{n}^{d}$
,
$\operatorname {os}_{n}^{d}$
,
![]() $A_n^d$
,
$A_n^d$
,
![]() ${\mathcal {M}}_n^d$
and
${\mathcal {M}}_n^d$
and
![]() $M_x$
from Section 5.1.
$M_x$
from Section 5.1.
A (connected) Kupisch series of type
![]() $\mathbb {A}_n$
is a tuple
$\mathbb {A}_n$
is a tuple
![]() $\underline {\ell }=(\ell _0,\ell _1,\dots , \ell _{n-1})$
of positive integers satisfying
$\underline {\ell }=(\ell _0,\ell _1,\dots , \ell _{n-1})$
of positive integers satisfying
Given such a Kupisch series
![]() $\underline {\ell }$
, consider the subset
$\underline {\ell }$
, consider the subset
where
![]() $\ell \ell (y)=y_d-y_0+1$
. Note that
$\ell \ell (y)=y_d-y_0+1$
. Note that
![]() $\ell \ell (y)$
is equal to the Loewy length of the module
$\ell \ell (y)$
is equal to the Loewy length of the module
![]() $M_y$
in
$M_y$
in
![]() $\operatorname {mod}A_n^d$
; see [Reference Jasso, Külshammer, Psaroudakis and KvammeJKPK, Lemma 2.9]. For
$\operatorname {mod}A_n^d$
; see [Reference Jasso, Külshammer, Psaroudakis and KvammeJKPK, Lemma 2.9]. For
![]() $d\geq 2$
, the d-th Nakayama algebra with Kupisch series
$d\geq 2$
, the d-th Nakayama algebra with Kupisch series
![]() $\underline {\ell }$
is the idempotent quotient
$\underline {\ell }$
is the idempotent quotient
In other words, if we let
![]() $e_{\underline {\ell }}$
be the idempotent consisting of the sum of the vertices in
$e_{\underline {\ell }}$
be the idempotent consisting of the sum of the vertices in
![]() $\operatorname {os}_{n}^{d}\setminus \operatorname {os}_{\underline {\ell }}^{d}$
, then
$\operatorname {os}_{n}^{d}\setminus \operatorname {os}_{\underline {\ell }}^{d}$
, then
![]() $A_{\underline {\ell }}^d$
is isomorphic to
$A_{\underline {\ell }}^d$
is isomorphic to
![]() $A_n^d/A_n^d e_{\underline {\ell }}A_n^d$
. It follows from [Reference Jasso, Külshammer, Psaroudakis and KvammeJKPK, Proposition 2.24] that the subcategory
$A_n^d/A_n^d e_{\underline {\ell }}A_n^d$
. It follows from [Reference Jasso, Külshammer, Psaroudakis and KvammeJKPK, Proposition 2.24] that the subcategory ![]() is d-cluster tilting in
is d-cluster tilting in
![]() $\operatorname {mod}A_{\underline {\ell }}^d$
, and that
$\operatorname {mod}A_{\underline {\ell }}^d$
, and that
![]() ${\mathcal {M}}_{\underline {\ell }}^d=\operatorname {add}\,(M_{\underline {\ell }}^d)$
for
${\mathcal {M}}_{\underline {\ell }}^d=\operatorname {add}\,(M_{\underline {\ell }}^d)$
for
![]() $M_{\underline {\ell }}^d=\bigoplus _{x\in \operatorname {os}_{\underline {\ell }}^{d+1}}M_x$
.
$M_{\underline {\ell }}^d=\bigoplus _{x\in \operatorname {os}_{\underline {\ell }}^{d+1}}M_x$
.
Note that the isomorphism classes of indecomposable modules in
![]() ${\mathcal {M}}_{\underline {\ell }}^d$
are in bijection with elements of
${\mathcal {M}}_{\underline {\ell }}^d$
are in bijection with elements of
![]() $\operatorname {os}_{\underline {\ell }}^{d+1}$
. Using our results, we can characterise the subsets of
$\operatorname {os}_{\underline {\ell }}^{d+1}$
. Using our results, we can characterise the subsets of
![]() $\operatorname {os}_{\underline {\ell }}^{d+1}$
which correspond to higher torsion classes in
$\operatorname {os}_{\underline {\ell }}^{d+1}$
which correspond to higher torsion classes in
![]() ${\mathcal {M}}_{\underline {\ell }}^d$
. We use the notation
${\mathcal {M}}_{\underline {\ell }}^d$
. We use the notation
for the subcategory of
![]() ${\mathcal {M}}_{\underline {\ell }}^d$
associated to a subset
${\mathcal {M}}_{\underline {\ell }}^d$
associated to a subset
![]() $I \subseteq \operatorname {os}_{\underline {\ell }}^{d+1}$
.
$I \subseteq \operatorname {os}_{\underline {\ell }}^{d+1}$
.
Theorem 6.1. Let
![]() $\underline {\ell }$
be a Kupisch series of type
$\underline {\ell }$
be a Kupisch series of type
![]() $\mathbb {A}_n$
and consider a subset
$\mathbb {A}_n$
and consider a subset
![]() $I \subseteq \operatorname {os}_{\underline {\ell }}^{d+1}$
. The subcategory
$I \subseteq \operatorname {os}_{\underline {\ell }}^{d+1}$
. The subcategory
![]() $\mathcal {U}_I$
is a d-torsion class in
$\mathcal {U}_I$
is a d-torsion class in
![]() ${\mathcal {M}}_{\underline {\ell }}^d$
if and only if the following hold for any elements
${\mathcal {M}}_{\underline {\ell }}^d$
if and only if the following hold for any elements
![]() $x,z\in \operatorname {os}_{\underline {\ell }}^{d+1}$
:
$x,z\in \operatorname {os}_{\underline {\ell }}^{d+1}$
:
-
(1) If
 $x\leq z$
and
$x\leq z$
and
 $x_d=z_d$
, then
$x_d=z_d$
, then
 $x\in I$
implies
$x\in I$
implies
 $z\in I$
.
$z\in I$
. -
(2) If
 $x\rightsquigarrow \tau _d(z)$
and
$x\rightsquigarrow \tau _d(z)$
and
 $x,z\in I$
, then any
$x,z\in I$
, then any
 $y\in \operatorname {os}_{\underline {\ell }}^{d+1}$
with
$y\in \operatorname {os}_{\underline {\ell }}^{d+1}$
with
 $y_i \in \{x_i,z_i\}$
for each i must be in I.
$y_i \in \{x_i,z_i\}$
for each i must be in I.
Proof. By Corollary 5.12, condition (1) is equivalent to
![]() $\mathcal {U}_I$
being closed under d-quotients in
$\mathcal {U}_I$
being closed under d-quotients in
![]() $\mathcal {M}^d_{n}$
. For objects in
$\mathcal {M}^d_{n}$
. For objects in
![]() ${\mathcal {M}}_{\underline {\ell }}^d$
, the minimal d-quotients in
${\mathcal {M}}_{\underline {\ell }}^d$
, the minimal d-quotients in
![]() ${\mathcal {M}}_{\underline {\ell }}^d$
are the same as the minimal d-quotients in
${\mathcal {M}}_{\underline {\ell }}^d$
are the same as the minimal d-quotients in
![]() $\mathcal {M}^d_{n}$
by Proposition 4.7(3) and Remark 4.8. Hence, condition (1) is also equivalent to
$\mathcal {M}^d_{n}$
by Proposition 4.7(3) and Remark 4.8. Hence, condition (1) is also equivalent to
![]() $\mathcal {U}_I$
being closed under d-quotients in
$\mathcal {U}_I$
being closed under d-quotients in
![]() ${\mathcal {M}}_{\underline {\ell }}^d$
.
${\mathcal {M}}_{\underline {\ell }}^d$
.
Note next that d-extensions in
![]() ${\mathcal {M}}_{\underline {\ell }}^d$
coincide with d-extensions in
${\mathcal {M}}_{\underline {\ell }}^d$
coincide with d-extensions in
![]() ${\mathcal {M}}_n^d$
with all terms in
${\mathcal {M}}_n^d$
with all terms in
![]() ${\mathcal {M}}_{\underline {\ell }}^d$
. By Proposition 5.3 and Remark 5.4, condition (2) hence implies that
${\mathcal {M}}_{\underline {\ell }}^d$
. By Proposition 5.3 and Remark 5.4, condition (2) hence implies that
![]() $\mathcal {U}_I$
is closed under d-extensions by indecomposables in
$\mathcal {U}_I$
is closed under d-extensions by indecomposables in
![]() ${\mathcal {M}}_{\underline {\ell }}^d$
. Assuming both (1) and (2) thus yields that
${\mathcal {M}}_{\underline {\ell }}^d$
. Assuming both (1) and (2) thus yields that
![]() $\mathcal {U}_I$
is closed under all d-extensions in
$\mathcal {U}_I$
is closed under all d-extensions in
![]() ${\mathcal {M}}_{\underline {\ell }}^d$
by Theorem 3.20, so
${\mathcal {M}}_{\underline {\ell }}^d$
by Theorem 3.20, so
![]() $\mathcal {U}_I$
is a d-torsion class in
$\mathcal {U}_I$
is a d-torsion class in
![]() ${\mathcal {M}}_{\underline {\ell }}^d$
by Theorem 3.17.
${\mathcal {M}}_{\underline {\ell }}^d$
by Theorem 3.17.
It remains to show that if
![]() $\mathcal {U}_I$
is a d-torsion class in
$\mathcal {U}_I$
is a d-torsion class in
![]() ${\mathcal {M}}_{\underline {\ell }}^d$
, then condition (2) is satisfied. We will use that we already know condition (1) holds. Consider
${\mathcal {M}}_{\underline {\ell }}^d$
, then condition (2) is satisfied. We will use that we already know condition (1) holds. Consider
![]() $x, z\in I$
with
$x, z\in I$
with
![]() $x\rightsquigarrow \tau _d(z)$
, and suppose that
$x\rightsquigarrow \tau _d(z)$
, and suppose that
![]() $y\in \operatorname {os}_{\underline {\ell }}^{d+1}$
satisfies
$y\in \operatorname {os}_{\underline {\ell }}^{d+1}$
satisfies
![]() $y_i \in \{x_i,z_i\}$
for each i. We need to show that
$y_i \in \{x_i,z_i\}$
for each i. We need to show that
![]() $y \in I$
.
$y \in I$
.
As
![]() $x\rightsquigarrow \tau _d(z)$
, there is a minimal d-extension
$x\rightsquigarrow \tau _d(z)$
, there is a minimal d-extension
in
![]() ${\mathcal {M}}_n^d$
with
${\mathcal {M}}_n^d$
with
![]() $M_y$
as a direct summand in one of the middle terms by Proposition 5.3 and Remark 5.4. Let us first assume
$M_y$
as a direct summand in one of the middle terms by Proposition 5.3 and Remark 5.4. Let us first assume
![]() $z_d-x_0+1\leq \ell _{z_d}$
. Using that
$z_d-x_0+1\leq \ell _{z_d}$
. Using that
![]() $x, z\in \operatorname {os}_{\underline {\ell }}^{d+1}$
and
$x, z\in \operatorname {os}_{\underline {\ell }}^{d+1}$
and
![]() $x_0 \leq z_0-1$
, we see that all the terms in (11) are in
$x_0 \leq z_0-1$
, we see that all the terms in (11) are in
![]() ${\mathcal {M}}_{\underline {\ell }}^d$
in this case. Hence, we must have
${\mathcal {M}}_{\underline {\ell }}^d$
in this case. Hence, we must have
![]() $M_y\in \mathcal {U}_I$
and
$M_y\in \mathcal {U}_I$
and
![]() $y\in I$
as
$y\in I$
as
![]() $\mathcal {U}_I$
is closed under d-extensions in
$\mathcal {U}_I$
is closed under d-extensions in
![]() ${\mathcal {M}}_{\underline {\ell }}^d$
.
${\mathcal {M}}_{\underline {\ell }}^d$
.
Consider now the case
![]() $z_d-x_0+1> \ell _{z_d}$
. Note that we have
$z_d-x_0+1> \ell _{z_d}$
. Note that we have
![]() $x\leq y$
. If
$x\leq y$
. If
![]() $y_d=x_d$
, condition (1) hence yields that
$y_d=x_d$
, condition (1) hence yields that
![]() $y\in I$
, so we can assume
$y\in I$
, so we can assume
![]() $y_d=z_d$
. Now
$y_d=z_d$
. Now
![]() $y_0=x_0$
would contradict the assumption
$y_0=x_0$
would contradict the assumption
![]() $z_d-x_0+1> \ell _{z_d}$
as
$z_d-x_0+1> \ell _{z_d}$
as
![]() $y\in \operatorname {os}_{\underline {\ell }}^{d+1}$
, so we must have
$y\in \operatorname {os}_{\underline {\ell }}^{d+1}$
, so we must have
![]() $y_0=z_0$
.
$y_0=z_0$
.
If
![]() $y=z$
, we have
$y=z$
, we have
![]() $y\in I$
, so assume that
$y\in I$
, so assume that
![]() $y_i=x_i$
for some
$y_i=x_i$
for some
![]() $1\leq i\leq d-1$
. This ensures that
$1\leq i\leq d-1$
. This ensures that ![]() exists. Note that for
exists. Note that for
![]() $j<k$
, we have
$j<k$
, we have
![]() $z_{j-1}-1\geq x_j$
. Combining this with the inequality
$z_{j-1}-1\geq x_j$
. Combining this with the inequality
![]() $x_j \geq z_{j-1}-1$
coming from
$x_j \geq z_{j-1}-1$
coming from
![]() $x\rightsquigarrow \tau _d(z)$
, we get that
$x\rightsquigarrow \tau _d(z)$
, we get that
![]() $x_j=z_{j-1}-1$
for
$x_j=z_{j-1}-1$
for
![]() $j>0$
. Let
$j>0$
. Let
and observe that
![]() $w \in \operatorname {os}_{\underline {\ell }}^{d+1}$
with
$w \in \operatorname {os}_{\underline {\ell }}^{d+1}$
with
![]() $w\leq y$
and
$w\leq y$
and
![]() $w_d=y_d$
since y is of the form
$w_d=y_d$
since y is of the form
under our current assumptions. Consequently, it suffices to show that
![]() $w\in I$
, as this implies
$w\in I$
, as this implies
![]() $y \in I$
by condition (1).
$y \in I$
by condition (1).
To this end, define
 $$ \begin{align*} \overline{x}&=(z_0,z_1,\ldots, z_{k-1}, x_k, \ldots, x_d) \\ \overline{z}&=(z_0+1,z_1+1,\ldots, z_{k-1}+1, z_k, \ldots, z_d). \end{align*} $$
$$ \begin{align*} \overline{x}&=(z_0,z_1,\ldots, z_{k-1}, x_k, \ldots, x_d) \\ \overline{z}&=(z_0+1,z_1+1,\ldots, z_{k-1}+1, z_k, \ldots, z_d). \end{align*} $$
We see that
![]() $\overline {x},\overline {z} \in \operatorname {os}_{\underline {\ell }}^{d+1}$
. Observe moreover that
$\overline {x},\overline {z} \in \operatorname {os}_{\underline {\ell }}^{d+1}$
. Observe moreover that
![]() $x\leq \overline {x}$
with
$x\leq \overline {x}$
with
![]() $\overline {x}_d=x_d$
and
$\overline {x}_d=x_d$
and
![]() $z\leq \overline {z}$
with
$z\leq \overline {z}$
with
![]() $\overline {z}_d=z_d$
, so
$\overline {z}_d=z_d$
, so
![]() $\overline {x},\overline {z}\in I$
by condition (1). Furthermore, we have
$\overline {x},\overline {z}\in I$
by condition (1). Furthermore, we have
![]() $\overline {x}\rightsquigarrow \tau _d(\overline {z})$
and
$\overline {x}\rightsquigarrow \tau _d(\overline {z})$
and
![]() $w_i\in \{\overline {x}_i,\overline {z}_i\}$
for all i. Finally, notice that
$w_i\in \{\overline {x}_i,\overline {z}_i\}$
for all i. Finally, notice that
![]() $\overline {z}_d-\overline {x}_0+1=z_d-z_0+1\leq \ell _{\overline {z}_d}$
. It follows that
$\overline {z}_d-\overline {x}_0+1=z_d-z_0+1\leq \ell _{\overline {z}_d}$
. It follows that
![]() $w\in I$
by the same argument as earlier in this proof, and we can conclude that
$w\in I$
by the same argument as earlier in this proof, and we can conclude that
![]() $y \in I$
.
$y \in I$
.
The following example illustrates the use of Theorem 6.1.
Example 6.2. Fix
![]() $n=4$
,
$n=4$
,
![]() $d=2$
and
$d=2$
and
![]() $\underline {\ell } = (1,2,2,3)$
. The higher Nakayama algebra
$\underline {\ell } = (1,2,2,3)$
. The higher Nakayama algebra
![]() $A_{\underline {\ell }}^{2}$
has a
$A_{\underline {\ell }}^{2}$
has a
![]() $2$
-cluster tilting subcategory
$2$
-cluster tilting subcategory
![]() ${\mathcal {M}}_{\underline {\ell }}^{2}$
, whose associated quiver can be found in Figure 4. Note that we identify the indecomposable objects of
${\mathcal {M}}_{\underline {\ell }}^{2}$
, whose associated quiver can be found in Figure 4. Note that we identify the indecomposable objects of
![]() ${\mathcal {M}}_{\underline {\ell }}^{2}$
with
${\mathcal {M}}_{\underline {\ell }}^{2}$
with
![]() $\operatorname {os}_{\underline {\ell }}^{3}$
and that we use a shortened notation for the sake of simplicity. The following subcategories are examples of
$\operatorname {os}_{\underline {\ell }}^{3}$
and that we use a shortened notation for the sake of simplicity. The following subcategories are examples of
![]() $2$
-torsion classes in
$2$
-torsion classes in
![]() ${\mathcal {M}}_{\underline {\ell }}^{2}$
:
${\mathcal {M}}_{\underline {\ell }}^{2}$
:
-
○
 $\operatorname {add}\{0\}$
$\operatorname {add}\{0\}$
-
○
 ${\mathcal {M}}_{\underline {\ell }}^{2}$
${\mathcal {M}}_{\underline {\ell }}^{2}$
-
○
 $\operatorname {add} \{000, 133, 222, 223, 233, 333\}$
$\operatorname {add} \{000, 133, 222, 223, 233, 333\}$
-
○
 $\operatorname {add} \{112,113,122,123,222,133,223,233,333\}$
.
$\operatorname {add} \{112,113,122,123,222,133,223,233,333\}$
.
Remark 6.3. With the results in this section, we can extend Algorithms 5.15 and 5.18 to the higher Nakayama setting with a few changes:
-
○ The input needs to include the Kupisch series
 $\underline {\ell }$
.
$\underline {\ell }$
. -
○ Elements must be chosen from
 $\operatorname {os}_{\underline {\ell }}^{d+1}$
, rather than
$\operatorname {os}_{\underline {\ell }}^{d+1}$
, rather than
 $\operatorname {os}_n^{d+1}$
.
$\operatorname {os}_n^{d+1}$
.
We have implemented the extended algorithm in the Google Colab Notebook associated to this paper.Footnote 2
6.2 Higher Nakayama algebras of type
 $\mathbb {A}_\infty ^\infty $
$\mathbb {A}_\infty ^\infty $
The goal of this subsection is to further extend the combinatorial description of d-torsion classes to higher Nakayama algebras of type
![]() $\mathbb {A}_\infty ^\infty $
as introduced in [Reference Jasso, Külshammer, Psaroudakis and KvammeJKPK]. We start by giving a brief introduction to this class of algebras.
$\mathbb {A}_\infty ^\infty $
as introduced in [Reference Jasso, Külshammer, Psaroudakis and KvammeJKPK]. We start by giving a brief introduction to this class of algebras.

Figure 4 The quiver of the
![]() $2$
-cluster tilting subcategory
$2$
-cluster tilting subcategory
![]() ${\mathcal{M}}_{\underline{\ell}}^{2}$
in Example 6.2.
${\mathcal{M}}_{\underline{\ell}}^{2}$
in Example 6.2.
In contrast to earlier in this paper, we now need to consider quivers with infinitely many vertices. Hence, associated to a quiver with relations is a category
![]() $\mathcal {C}$
rather than an algebra. The objects of
$\mathcal {C}$
rather than an algebra. The objects of
![]() $\mathcal {C}$
are the vertices of the quiver, and a basis of the morphisms spaces are given by the arrows modulo the given relations. A right module over
$\mathcal {C}$
are the vertices of the quiver, and a basis of the morphisms spaces are given by the arrows modulo the given relations. A right module over
![]() $\mathcal {C}$
is a
$\mathcal {C}$
is a
![]() $\mathbb {k}$
-linear functor
$\mathbb {k}$
-linear functor
![]() $M\colon \mathcal {C}^{\operatorname {op}}\to \operatorname {Mod}\mathbb {k}$
. The module M is called finite-dimensional if the sum
$M\colon \mathcal {C}^{\operatorname {op}}\to \operatorname {Mod}\mathbb {k}$
. The module M is called finite-dimensional if the sum
![]() $\bigoplus _{x\in \mathcal {C}}M(x)$
is finite-dimensional. We let
$\bigoplus _{x\in \mathcal {C}}M(x)$
is finite-dimensional. We let
![]() $\operatorname {fd}\mathcal {C}$
denote the category of finite-dimensional right modules over
$\operatorname {fd}\mathcal {C}$
denote the category of finite-dimensional right modules over
![]() $\mathcal {C}$
. For more details, see [Reference Jasso, Külshammer, Psaroudakis and KvammeJKPK, Sections 1.1 and 1.2].
$\mathcal {C}$
. For more details, see [Reference Jasso, Külshammer, Psaroudakis and KvammeJKPK, Sections 1.1 and 1.2].
Let
![]() $\operatorname {os}^d$
denote the set of non-decreasing d-tuples
$\operatorname {os}^d$
denote the set of non-decreasing d-tuples
![]() $x=(x_0,\dots , x_{d-1})$
over
$x=(x_0,\dots , x_{d-1})$
over
![]() $\mathbb {Z}$
. Consider
$\mathbb {Z}$
. Consider
![]() $\mathbb {Z}^d$
as a
$\mathbb {Z}^d$
as a
![]() $\mathbb {k}$
-linear category given by the
$\mathbb {k}$
-linear category given by the
![]() $\mathbb {k}$
-linearisation of the poset
$\mathbb {k}$
-linearisation of the poset
![]() $\mathbb {Z}^d$
endowed with the product order. The mesh category of type
$\mathbb {Z}^d$
endowed with the product order. The mesh category of type
![]() $\mathbb {Z}\mathbb {A}_\infty ^{d-1}$
is defined to be the additive quotient
$\mathbb {Z}\mathbb {A}_\infty ^{d-1}$
is defined to be the additive quotient
Note that
![]() $A_\infty ^{d}$
can be represented by the opposite of an infinite quiver
$A_\infty ^{d}$
can be represented by the opposite of an infinite quiver
![]() $Q^{d}$
with relations. The vertices of
$Q^{d}$
with relations. The vertices of
![]() $Q^d$
are elements in
$Q^d$
are elements in
![]() $\operatorname {os}^d$
, and there is an arrow from vertex x to vertex y if
$\operatorname {os}^d$
, and there is an arrow from vertex x to vertex y if
![]() $y_i = x_i + 1$
for exactly one
$y_i = x_i + 1$
for exactly one
![]() $i= 0,\ldots , d-1$
and
$i= 0,\ldots , d-1$
and
![]() $y_j = x_j$
for
$y_j = x_j$
for
![]() $j\neq i$
. The relations of
$j\neq i$
. The relations of
![]() $A_\infty ^{d}$
are given by a certain admissible ideal making squares commutative and sending certain compositions of two arrows to zero; see [Reference Jasso, Külshammer, Psaroudakis and KvammeJKPK, Section 3.1] for more details.
$A_\infty ^{d}$
are given by a certain admissible ideal making squares commutative and sending certain compositions of two arrows to zero; see [Reference Jasso, Külshammer, Psaroudakis and KvammeJKPK, Section 3.1] for more details.
Following [Reference Jasso, Külshammer, Psaroudakis and KvammeJKPK, Appendix Reference BridgelandB], we say that a Kupisch series of type
![]() $\mathbb {A}_\infty ^\infty $
is an infinite tuple
$\mathbb {A}_\infty ^\infty $
is an infinite tuple
![]() $\underline {\ell } =(\dots , \ell _{-1}, \ell _0, \ell _1, \dots )$
, where
$\underline {\ell } =(\dots , \ell _{-1}, \ell _0, \ell _1, \dots )$
, where
![]() $\ell _i$
is either a nonnegative integer or equal to
$\ell _i$
is either a nonnegative integer or equal to
![]() $\infty $
, and where the inequality
$\infty $
, and where the inequality
holds for all
![]() $i\in \mathbb {Z}$
. We write
$i\in \mathbb {Z}$
. We write
![]() $\operatorname {KS}(\mathbb {A}_\infty ^\infty )$
for the set of Kupisch series of type
$\operatorname {KS}(\mathbb {A}_\infty ^\infty )$
for the set of Kupisch series of type
![]() $\mathbb {A}_\infty ^\infty $
. Given such a Kupisch series
$\mathbb {A}_\infty ^\infty $
. Given such a Kupisch series
![]() $\underline {\ell }$
, define the subset
$\underline {\ell }$
, define the subset
where
![]() $\ell \ell (y)=y_d-y_0+1$
as before. For
$\ell \ell (y)=y_d-y_0+1$
as before. For
![]() $d\geq 2$
, the category
$d\geq 2$
, the category
![]() $A_{\underline {\ell }}^d$
is defined as the idempotent quotient
$A_{\underline {\ell }}^d$
is defined as the idempotent quotient
Note that we have an inclusion
![]() $\operatorname {fd}A_{\underline {\ell }}^d\to \operatorname {fd}A_\infty ^d$
between the categories of finite-dimensional modules. Associated to the Kupisch series
$\operatorname {fd}A_{\underline {\ell }}^d\to \operatorname {fd}A_\infty ^d$
between the categories of finite-dimensional modules. Associated to the Kupisch series
![]() $\underline {\ell }$
, we also have the subcategory
$\underline {\ell }$
, we also have the subcategory
of
![]() $\operatorname {fd}A_\infty ^d$
. Here, we use the notation
$\operatorname {fd}A_\infty ^d$
. Here, we use the notation
![]() $M_x$
for the indecomposable
$M_x$
for the indecomposable
![]() $A_\infty ^d$
-module with support in all vertices
$A_\infty ^d$
-module with support in all vertices
![]() $y\in \operatorname {os}^d$
satisfying
$y\in \operatorname {os}^d$
satisfying
![]() $x_0\leq y_0\leq x_1\leq \cdots \leq x_{d-1}\leq y_{d-1}\leq x_d$
. This extends the analogous definition in Section 5.1. By [Reference Jasso, Külshammer, Psaroudakis and KvammeJKPK, Appendix Reference BridgelandB], the subcategory
$x_0\leq y_0\leq x_1\leq \cdots \leq x_{d-1}\leq y_{d-1}\leq x_d$
. This extends the analogous definition in Section 5.1. By [Reference Jasso, Külshammer, Psaroudakis and KvammeJKPK, Appendix Reference BridgelandB], the subcategory
![]() ${\mathcal {M}}_{\underline {\ell }}^d$
is d-cluster tilting in
${\mathcal {M}}_{\underline {\ell }}^d$
is d-cluster tilting in
![]() $\operatorname {fd}A_{\underline {\ell }}^d$
. For certain choices of
$\operatorname {fd}A_{\underline {\ell }}^d$
. For certain choices of
![]() $\underline {\ell }$
, this gives an example of a d-cluster tilting subcategory of an abelian category with no nonzero projective or injective objects (e.g., if
$\underline {\ell }$
, this gives an example of a d-cluster tilting subcategory of an abelian category with no nonzero projective or injective objects (e.g., if
![]() $\ell _i=\infty $
for all
$\ell _i=\infty $
for all
![]() $i\in \mathbb {Z}$
); see [Reference Jasso, Külshammer, Psaroudakis and KvammeJKPK, Proposition 3.6].
$i\in \mathbb {Z}$
); see [Reference Jasso, Külshammer, Psaroudakis and KvammeJKPK, Proposition 3.6].
Now consider the partial order on the set
![]() $\operatorname {KS}(\mathbb {A}_\infty ^\infty )$
given by the product order. If
$\operatorname {KS}(\mathbb {A}_\infty ^\infty )$
given by the product order. If
![]() $\underline {\ell }\leq \underline {\ell '}$
, then we have a natural functor
$\underline {\ell }\leq \underline {\ell '}$
, then we have a natural functor
![]() $A_{\underline {\ell }'}^d\to A_{\underline {\ell }}^d$
of categories. This gives an inclusion
$A_{\underline {\ell }'}^d\to A_{\underline {\ell }}^d$
of categories. This gives an inclusion
![]() $\operatorname {fd}A_{\underline {\ell }}^d\to \operatorname {fd}A_{\underline {\ell }'}^d$
such that the equality
$\operatorname {fd}A_{\underline {\ell }}^d\to \operatorname {fd}A_{\underline {\ell }'}^d$
such that the equality
holds. Similarly, if
![]() $\underline {\ell }^1\leq \underline {\ell }^2\leq \cdots $
is an increasing sequence of Kupisch series which converges to
$\underline {\ell }^1\leq \underline {\ell }^2\leq \cdots $
is an increasing sequence of Kupisch series which converges to
![]() $\underline {\ell }\in \operatorname {KS}(\mathbb {A}_\infty ^\infty )$
(in the natural way), then
$\underline {\ell }\in \operatorname {KS}(\mathbb {A}_\infty ^\infty )$
(in the natural way), then
A Kupisch series
![]() $\underline {\ell }\in \operatorname {KS}(\mathbb {A}_\infty ^\infty )$
is called finite if
$\underline {\ell }\in \operatorname {KS}(\mathbb {A}_\infty ^\infty )$
is called finite if
![]() $\ell _j=0$
for all but finitely many
$\ell _j=0$
for all but finitely many
![]() $j\in \mathbb {Z}$
. Note that for any
$j\in \mathbb {Z}$
. Note that for any
![]() $\underline {\ell }\in \operatorname {KS}(\mathbb {A}_\infty ^\infty )$
, we can find a sequence
$\underline {\ell }\in \operatorname {KS}(\mathbb {A}_\infty ^\infty )$
, we can find a sequence
![]() $\underline {\ell }^1\leq \underline {\ell }^2\leq \cdots $
of finite Kupisch series in
$\underline {\ell }^1\leq \underline {\ell }^2\leq \cdots $
of finite Kupisch series in
![]() $\operatorname {KS}(\mathbb {A}_\infty ^\infty )$
which converges to
$\operatorname {KS}(\mathbb {A}_\infty ^\infty )$
which converges to
![]() $\underline {\ell }$
. We use this to give a characterisation of the d-torsion classes in
$\underline {\ell }$
. We use this to give a characterisation of the d-torsion classes in
![]() ${\mathcal {M}}_{\underline {\ell }}^d$
in Theorem 6.5 below.
${\mathcal {M}}_{\underline {\ell }}^d$
in Theorem 6.5 below.
Remark 6.4. Let
![]() $\underline {\ell }$
be a Kupisch series of type
$\underline {\ell }$
be a Kupisch series of type
![]() $\mathbb {A}_n$
. Then
$\mathbb {A}_n$
. Then
![]() $\underline {\ell }$
can be identified with a finite Kupisch series
$\underline {\ell }$
can be identified with a finite Kupisch series
![]() $\underline {\ell }'$
of type
$\underline {\ell }'$
of type
![]() $\mathbb {A}_\infty ^\infty $
which is nonzero only in positions
$\mathbb {A}_\infty ^\infty $
which is nonzero only in positions
![]() $0,\ldots , n-1$
. In this case, there is a bijection between the sets
$0,\ldots , n-1$
. In this case, there is a bijection between the sets
![]() $\operatorname {os}_{\underline {\ell }}^{d}$
and
$\operatorname {os}_{\underline {\ell }}^{d}$
and
![]() $\operatorname {os}_{\underline {\ell }'}^{d}$
, so the algebra
$\operatorname {os}_{\underline {\ell }'}^{d}$
, so the algebra
![]() $A^d_{\underline {\ell }}$
and the category
$A^d_{\underline {\ell }}$
and the category
![]() $A^d_{\underline {\ell }'}$
can be naturally identified. Note that up to isomorphism, the set
$A^d_{\underline {\ell }'}$
can be naturally identified. Note that up to isomorphism, the set
![]() $\operatorname {os}_{\underline {\ell }'}^{d}$
and the category
$\operatorname {os}_{\underline {\ell }'}^{d}$
and the category
![]() $A^d_{\underline {\ell }'}$
remain unchanged when shifting
$A^d_{\underline {\ell }'}$
remain unchanged when shifting
![]() $\underline {\ell }'$
some number of steps to the left or right.
$\underline {\ell }'$
some number of steps to the left or right.
In general, if
![]() $\underline {\ell }$
is a finite Kupisch series of type
$\underline {\ell }$
is a finite Kupisch series of type
![]() $\mathbb {A}^\infty _\infty $
, then
$\mathbb {A}^\infty _\infty $
, then
![]() $\underline {\ell }$
is obtained by gluing together shifts of Kupisch series of type
$\underline {\ell }$
is obtained by gluing together shifts of Kupisch series of type
![]() $\mathbb {A}$
. Hence, the set
$\mathbb {A}$
. Hence, the set
![]() $\operatorname {os}^d_{\underline {\ell }}$
is in bijection with a disjoint union
$\operatorname {os}^d_{\underline {\ell }}$
is in bijection with a disjoint union
![]() $\bigcup _{j=1}^m\operatorname {os}^d_{\underline {\ell }_j}$
where
$\bigcup _{j=1}^m\operatorname {os}^d_{\underline {\ell }_j}$
where
![]() $\underline {\ell }_j$
is a Kupisch series of type
$\underline {\ell }_j$
is a Kupisch series of type
![]() $\mathbb {A}_{n_j}$
for some integer
$\mathbb {A}_{n_j}$
for some integer
![]() $n_j\geq 1$
. The associated category
$n_j\geq 1$
. The associated category
![]() $A^d_{\underline {\ell }}$
can thus be identified with a finite product
$A^d_{\underline {\ell }}$
can thus be identified with a finite product
where
![]() $A^d_{\underline {\ell }_j}$
is a higher Nakayama algebras of type
$A^d_{\underline {\ell }_j}$
is a higher Nakayama algebras of type
![]() $\mathbb {A}_{n_j}$
. With this identification, the category
$\mathbb {A}_{n_j}$
. With this identification, the category
![]() $\operatorname {fd}A^d_{\underline {\ell }}$
is equivalent to the product
$\operatorname {fd}A^d_{\underline {\ell }}$
is equivalent to the product
![]() $\operatorname {mod}A^d_{\underline {\ell }_1}\times \cdots \times \operatorname {mod}A^d_{\underline {\ell }_m}$
, and the d-cluster tilting subcategory
$\operatorname {mod}A^d_{\underline {\ell }_1}\times \cdots \times \operatorname {mod}A^d_{\underline {\ell }_m}$
, and the d-cluster tilting subcategory
![]() $\mathcal {M}^d_{\underline {\ell }}$
is equivalent to the product
$\mathcal {M}^d_{\underline {\ell }}$
is equivalent to the product
![]() $\mathcal {M}^d_{\underline {\ell }_1}\times \cdots \times \mathcal {M}^d_{\underline {\ell }_m}$
. Since any Kupisch series
$\mathcal {M}^d_{\underline {\ell }_1}\times \cdots \times \mathcal {M}^d_{\underline {\ell }_m}$
. Since any Kupisch series
![]() $\underline {\ell }$
of type
$\underline {\ell }$
of type
![]() $\mathbb {A}_\infty ^\infty $
can be represented by a converging sequence of finite Kupisch series, it follows that the associated d-cluster tilting subcategory
$\mathbb {A}_\infty ^\infty $
can be represented by a converging sequence of finite Kupisch series, it follows that the associated d-cluster tilting subcategory
![]() ${\mathcal {M}}_{\underline {\ell }}^d$
is the union of finite products of d-cluster tilting subcategories of higher Nakayama algebras of type
${\mathcal {M}}_{\underline {\ell }}^d$
is the union of finite products of d-cluster tilting subcategories of higher Nakayama algebras of type
![]() $\mathbb {A}$
.
$\mathbb {A}$
.
As before, we use the notation
for the subcategory of
![]() ${\mathcal {M}}_{\underline {\ell }}^d$
associated to a subset
${\mathcal {M}}_{\underline {\ell }}^d$
associated to a subset
![]() $I \subseteq \operatorname {os}_{\underline {\ell }}^{d+1}$
.
$I \subseteq \operatorname {os}_{\underline {\ell }}^{d+1}$
.
Theorem 6.5. Let
![]() $\underline {\ell }$
be a Kupisch series of type
$\underline {\ell }$
be a Kupisch series of type
![]() $\mathbb {A}_\infty ^\infty $
and consider a subset
$\mathbb {A}_\infty ^\infty $
and consider a subset
![]() $I \subseteq \operatorname {os}_{\underline {\ell }}^{d+1}$
. The subcategory
$I \subseteq \operatorname {os}_{\underline {\ell }}^{d+1}$
. The subcategory
![]() $\mathcal {U}_I$
is a d-torsion class in
$\mathcal {U}_I$
is a d-torsion class in
![]() ${\mathcal {M}}_{\underline {\ell }}^d$
if and only if the following hold for any elements
${\mathcal {M}}_{\underline {\ell }}^d$
if and only if the following hold for any elements
![]() $x,z\in \operatorname {os}_{\underline {\ell }}^{d+1}$
:
$x,z\in \operatorname {os}_{\underline {\ell }}^{d+1}$
:
-
(1) If
 $x\leq z$
and
$x\leq z$
and
 $x_d=z_d$
, then
$x_d=z_d$
, then
 $x\in I$
implies
$x\in I$
implies
 $z\in I$
.
$z\in I$
. -
(2) If
 $x\rightsquigarrow \tau _d(z)$
and
$x\rightsquigarrow \tau _d(z)$
and
 $x,z\in I$
, then any
$x,z\in I$
, then any
 $y\in \operatorname {os}_{\underline {\ell }}^{d+1}$
with
$y\in \operatorname {os}_{\underline {\ell }}^{d+1}$
with
 $y_i \in \{x_i,z_i\}$
for each i must be in I.
$y_i \in \{x_i,z_i\}$
for each i must be in I.
Proof. Choose an increasing sequence
![]() $\underline {\ell }^1\leq \underline {\ell }^2\leq \cdots $
of finite Kupisch series which converges to
$\underline {\ell }^1\leq \underline {\ell }^2\leq \cdots $
of finite Kupisch series which converges to
![]() $\underline {\ell }$
. Then we have that
$\underline {\ell }$
. Then we have that
for each
![]() $i \geq 1$
. Fix
$i \geq 1$
. Fix
![]() $i\geq 1$
, and set
$i\geq 1$
, and set
![]() $J^i=I\cap \operatorname {os}_{\underline {\ell }^i}^{d+1}$
. We have an equivalence between
$J^i=I\cap \operatorname {os}_{\underline {\ell }^i}^{d+1}$
. We have an equivalence between
![]() $\mathcal {M}^d_{\underline {\ell }^i}$
and a finite product
$\mathcal {M}^d_{\underline {\ell }^i}$
and a finite product
![]() $\mathcal {M}^d_{\underline {\ell }^i_1}\times \cdots \times \mathcal {M}^d_{\underline {\ell }^i_m}$
as in Remark 6.4. The subcategory
$\mathcal {M}^d_{\underline {\ell }^i_1}\times \cdots \times \mathcal {M}^d_{\underline {\ell }^i_m}$
as in Remark 6.4. The subcategory
![]() $\mathcal {U}_{J^i}$
of
$\mathcal {U}_{J^i}$
of
![]() $\mathcal {M}^d_{\underline {\ell }^i}$
is hence equivalent to a product
$\mathcal {M}^d_{\underline {\ell }^i}$
is hence equivalent to a product
![]() $\mathcal {U}_1\times \cdots \times \mathcal {U}_m$
, where
$\mathcal {U}_1\times \cdots \times \mathcal {U}_m$
, where
![]() $\mathcal {U}_k$
is a subcategory of
$\mathcal {U}_k$
is a subcategory of
![]() $\mathcal {M}^d_{\underline {\ell }^i_k}$
for each k. Note that
$\mathcal {M}^d_{\underline {\ell }^i_k}$
for each k. Note that
![]() $\operatorname {os}_{\underline {\ell }^i}^{d+1}$
is in bijection with the disjoint union
$\operatorname {os}_{\underline {\ell }^i}^{d+1}$
is in bijection with the disjoint union
![]() $\bigcup _{k=1}^m\operatorname {os}^{d+1}_{\underline {\ell }^i_k}$
as in Remark 6.4. We let
$\bigcup _{k=1}^m\operatorname {os}^{d+1}_{\underline {\ell }^i_k}$
as in Remark 6.4. We let
![]() $J^i_k$
denote the intersection of
$J^i_k$
denote the intersection of
![]() $\operatorname {os}^{d+1}_{\underline {\ell }^i_k}$
with the image of
$\operatorname {os}^{d+1}_{\underline {\ell }^i_k}$
with the image of
![]() $J^i$
under this bijection. Then we get
$J^i$
under this bijection. Then we get
![]() $\mathcal {U}_k=\mathcal {U}_{J^i_k}$
.
$\mathcal {U}_k=\mathcal {U}_{J^i_k}$
.
Note that I satisfies the conditions (1) and (2) in the statement if and only if the set
![]() $J^i$
satisfies the analogous conditions for each
$J^i$
satisfies the analogous conditions for each
![]() $i\geq 1$
. Furthermore, this holds if and only if each
$i\geq 1$
. Furthermore, this holds if and only if each
![]() $J^i_k$
satisfies the conditions of Theorem 6.1. By Theorem 6.1, this is again equivalent to
$J^i_k$
satisfies the conditions of Theorem 6.1. By Theorem 6.1, this is again equivalent to
![]() $\mathcal {U}_{J^i_k}$
being a d-torsion class in
$\mathcal {U}_{J^i_k}$
being a d-torsion class in
![]() $\mathcal {M}^d_{\underline {\ell }^i_k}$
for all i and k (i.e., that
$\mathcal {M}^d_{\underline {\ell }^i_k}$
for all i and k (i.e., that
![]() $\mathcal {U}_{J^i} \simeq \mathcal {U}_{J^i_1}\times \cdots \times \mathcal {U}_{J^i_m}$
is a d-torsion class in
$\mathcal {U}_{J^i} \simeq \mathcal {U}_{J^i_1}\times \cdots \times \mathcal {U}_{J^i_m}$
is a d-torsion class in
![]() ${\mathcal {M}}_{\underline {\ell }^i}^d$
for all
${\mathcal {M}}_{\underline {\ell }^i}^d$
for all
![]() $i\geq 1$
). Hence, it suffices to show that
$i\geq 1$
). Hence, it suffices to show that
![]() $\mathcal {U}_I$
is a d-torsion class in
$\mathcal {U}_I$
is a d-torsion class in
![]() ${\mathcal {M}}_{\underline {\ell }}^d$
if and only if
${\mathcal {M}}_{\underline {\ell }}^d$
if and only if
![]() $\mathcal {U}_{J^i}$
is a d-torsion class in
$\mathcal {U}_{J^i}$
is a d-torsion class in
![]() ${\mathcal {M}}_{\underline {\ell }^i}^d$
for all
${\mathcal {M}}_{\underline {\ell }^i}^d$
for all
![]() $i\geq 1$
.
$i\geq 1$
.
If
![]() $\mathcal {U}_I$
is a d-torsion class in
$\mathcal {U}_I$
is a d-torsion class in
![]() ${\mathcal {M}}_{\underline {\ell }}^d$
, then
${\mathcal {M}}_{\underline {\ell }}^d$
, then
![]() $\mathcal {U}_{J^i}=\mathcal {U}_I\cap \mathcal {M}^d_{\underline {\ell }^i}$
is a d-torsion class in
$\mathcal {U}_{J^i}=\mathcal {U}_I\cap \mathcal {M}^d_{\underline {\ell }^i}$
is a d-torsion class in
![]() ${\mathcal {M}}_{\underline {\ell }^i}^d={\mathcal {M}}_{\underline {\ell }}^d\cap \operatorname {fd}A_{\underline {\ell }^i}^d$
for all
${\mathcal {M}}_{\underline {\ell }^i}^d={\mathcal {M}}_{\underline {\ell }}^d\cap \operatorname {fd}A_{\underline {\ell }^i}^d$
for all
![]() $i\geq 1$
by Proposition 4.7(1). Conversely, assume
$i\geq 1$
by Proposition 4.7(1). Conversely, assume
![]() $\mathcal {U}_{J^i}$
is a d-torsion class in
$\mathcal {U}_{J^i}$
is a d-torsion class in
![]() ${\mathcal {M}}_{\underline {\ell }^i}^d$
for all
${\mathcal {M}}_{\underline {\ell }^i}^d$
for all
![]() $i\geq 1$
. Since we have
$i\geq 1$
. Since we have
the subcategory
![]() $\mathcal {U}_I$
must be closed both under d-extensions and d-quotients in
$\mathcal {U}_I$
must be closed both under d-extensions and d-quotients in
![]() ${\mathcal {M}}_{\underline {\ell }}^d=\bigcup _{i\geq 1}{\mathcal {M}}_{\underline {\ell }^i}^d$
, since
${\mathcal {M}}_{\underline {\ell }}^d=\bigcup _{i\geq 1}{\mathcal {M}}_{\underline {\ell }^i}^d$
, since
![]() $\mathcal {U}_{J^i}$
is closed under d-extensions and d-quotients in
$\mathcal {U}_{J^i}$
is closed under d-extensions and d-quotients in
![]() ${\mathcal {M}}_{\underline {\ell }^i}^d$
for all
${\mathcal {M}}_{\underline {\ell }^i}^d$
for all
![]() $i \geq 1$
. By Theorem 3.17, this shows that
$i \geq 1$
. By Theorem 3.17, this shows that
![]() $\mathcal {U}_I$
is a d-torsion class.
$\mathcal {U}_I$
is a d-torsion class.
Acknowledgements
This project was started while the authors participated in the Junior Trimester Program ‘New Trends in Representation Theory’ at the Hausdorff Research Institute for Mathematics in Bonn. We thank the Institute for their hospitality and inspiring working conditions.
We are grateful to J. Asadollahi, P. Jørgensen and S. Schroll for allowing HT to share the ideas of [Reference Asadollahi, Jørgensen, Schroll and TreffingerAJST] even before the first draft of that paper was finished. Without their generosity, this project would not have started. We thank S. Land for help with coding optimization. We would also like to thank the anonymous referee for their careful reading and helpful comments.
JA was supported by the Max Planck Institute of Mathematics, and a DNRF Chair from the Danish National Research Foundation (grant no. DNRF156). JA, KMJ and SK would like to thank the Centre for Advanced Study in Oslo, where parts of this work were done.
Parts of this work were carried out while JH visited Aarhus University. She would like to thank the university for the hospitality and the project ‘Pure Mathematics in Norway’ funded by the Trond Mohn Foundation for supporting the stay.
KMJ was funded by the Norwegian Research Council via the project ‘Higher homological algebra and tilting theory’ (301046).
YP was supported by the French grant CHARMS (ANR–19–CE40–0017).
HT was supported by the European Union’s Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement No 893654 and by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy Programme – EXC-2047/1 – 390685813.
Competing interests
The authors have no competing interest to declare.