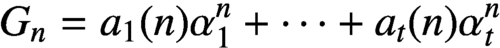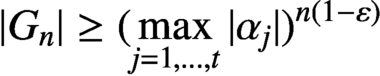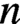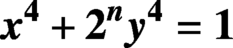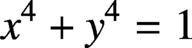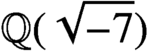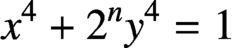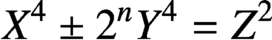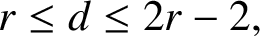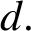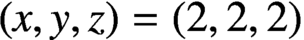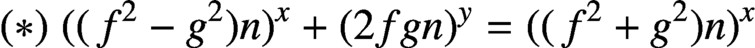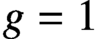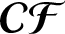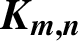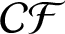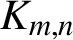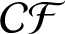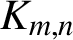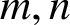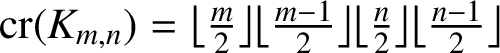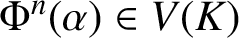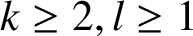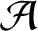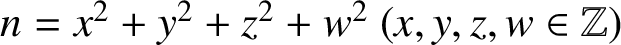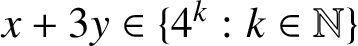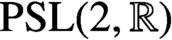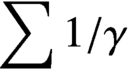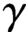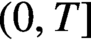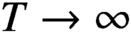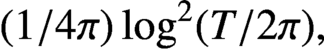Contents
Research Article
A NEW REFINEMENT OF FINE’S PARTITION THEOREM
- Part of:
-
- Published online by Cambridge University Press:
- 29 March 2021, pp. 353-361
-
- Article
- Export citation
BIASES IN INTEGER PARTITIONS
- Part of:
-
- Published online by Cambridge University Press:
- 14 January 2021, pp. 177-186
-
- Article
- Export citation
THE GENERAL POSITION NUMBER OF THE CARTESIAN PRODUCT OF TWO TREES
- Part of:
-
- Published online by Cambridge University Press:
- 04 December 2020, pp. 1-10
-
- Article
- Export citation
ASKING QUESTIONS TO DETERMINE THE PRODUCT OF CIRCULARLY ARRANGED NUMBERS
- Part of:
-
- Published online by Cambridge University Press:
- 19 April 2021, pp. 187-195
-
- Article
- Export citation
ON WEAKLY PERFECT ANNIHILATING-IDEAL GRAPHS
- Part of:
-
- Published online by Cambridge University Press:
- 11 May 2021, pp. 362-372
-
- Article
- Export citation
ON THE GROWTH OF LINEAR RECURRENCES IN FUNCTION FIELDS
- Part of:
-
- Published online by Cambridge University Press:
- 09 November 2020, pp. 11-20
-
- Article
-
- You have access
- Open access
- Export citation
THE DIOPHANTINE EQUATION
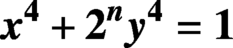 $\boldsymbol{x}^{\boldsymbol{4}} \boldsymbol{+} \boldsymbol{2}^{\boldsymbol{n}}\boldsymbol{y}^{\boldsymbol{4}} \boldsymbol{=} \boldsymbol{1}$ IN QUADRATIC NUMBER FIELDS
$\boldsymbol{x}^{\boldsymbol{4}} \boldsymbol{+} \boldsymbol{2}^{\boldsymbol{n}}\boldsymbol{y}^{\boldsymbol{4}} \boldsymbol{=} \boldsymbol{1}$ IN QUADRATIC NUMBER FIELDS
- Part of:
-
- Published online by Cambridge University Press:
- 06 November 2020, pp. 21-28
-
- Article
- Export citation
ADDITIVE BASES AND NIVEN NUMBERS
- Part of:
-
- Published online by Cambridge University Press:
- 25 March 2021, pp. 373-380
-
- Article
- Export citation
THE DIAMETER AND RADIUS OF RADIALLY MAXIMAL GRAPHS
- Part of:
-
- Published online by Cambridge University Press:
- 11 January 2021, pp. 196-202
-
- Article
- Export citation
A NOTE ON JEŚMANOWICZ’ CONJECTURE CONCERNING NONPRIMITIVE PYTHAGOREAN TRIPLES
- Part of:
-
- Published online by Cambridge University Press:
- 21 October 2020, pp. 29-39
-
- Article
- Export citation
ON PROBLEMS OF
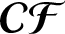 $\boldsymbol{\mathcal{CF}}$-CONNECTED GRAPHS FOR
$\boldsymbol{\mathcal{CF}}$-CONNECTED GRAPHS FOR 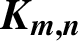 $\boldsymbol{K}_{\boldsymbol{m,n}}$
$\boldsymbol{K}_{\boldsymbol{m,n}}$
- Part of:
-
- Published online by Cambridge University Press:
- 01 December 2020, pp. 203-210
-
- Article
- Export citation
A SPARSITY RESULT FOR THE DYNAMICAL MORDELL–LANG CONJECTURE IN POSITIVE CHARACTERISTIC
- Part of:
-
- Published online by Cambridge University Press:
- 23 February 2021, pp. 381-390
-
- Article
- Export citation
ON ASYMPTOTIC BASES WHICH HAVE DISTINCT SUBSET SUMS
- Part of:
-
- Published online by Cambridge University Press:
- 12 April 2021, pp. 211-217
-
- Article
- Export citation
NOTES ON THE K-RATIONAL DISTANCE PROBLEM
- Part of:
-
- Published online by Cambridge University Press:
- 01 December 2020, pp. 40-44
-
- Article
- Export citation
CHARACTERISTIC POLYNOMIALS OF SIMPLE ORDINARY ABELIAN VARIETIES OVER FINITE FIELDS
- Part of:
-
- Published online by Cambridge University Press:
- 19 February 2021, pp. 391-397
-
- Article
- Export citation
ON A WEIGHTED SUM OF MULTIPLE $\mathbf{{T}}$
 -VALUES OF FIXED WEIGHT AND DEPTH
-VALUES OF FIXED WEIGHT AND DEPTH
- Part of:
-
- Published online by Cambridge University Press:
- 19 March 2021, pp. 398-405
-
- Article
- Export citation
SUMS OF FOUR SQUARES WITH A CERTAIN RESTRICTION
- Part of:
-
- Published online by Cambridge University Press:
- 14 January 2021, pp. 218-227
-
- Article
- Export citation
ON GOOD APPROXIMATIONS AND THE BOWEN–SERIES EXPANSION
- Part of:
-
- Published online by Cambridge University Press:
- 25 January 2021, pp. 45-58
-
- Article
- Export citation
A HARMONIC SUM OVER NONTRIVIAL ZEROS OF THE RIEMANN ZETA-FUNCTION
- Part of:
-
- Published online by Cambridge University Press:
- 20 November 2020, pp. 59-65
-
- Article
- Export citation
ON THE SUM OF PARTS IN THE PARTITIONS OF n INTO DISTINCT PARTS
- Part of:
-
- Published online by Cambridge University Press:
- 11 December 2020, pp. 228-237
-
- Article
- Export citation