Article contents
A SPARSITY RESULT FOR THE DYNAMICAL MORDELL–LANG CONJECTURE IN POSITIVE CHARACTERISTIC
Published online by Cambridge University Press: 23 February 2021
Abstract
We prove a quantitative partial result in support of the dynamical Mordell–Lang conjecture (also known as the DML conjecture) in positive characteristic. More precisely, we show the following: given a field K of characteristic p, a semiabelian variety X defined over a finite subfield of K and endowed with a regular self-map 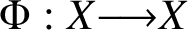 $\Phi :X{\longrightarrow } X$ defined over K, a point
$\Phi :X{\longrightarrow } X$ defined over K, a point 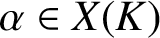 $\alpha \in X(K)$ and a subvariety
$\alpha \in X(K)$ and a subvariety 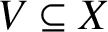 $V\subseteq X$, then the set of all nonnegative integers n such that
$V\subseteq X$, then the set of all nonnegative integers n such that 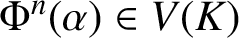 $\Phi ^n(\alpha )\in V(K)$ is a union of finitely many arithmetic progressions along with a subset S with the property that there exists a positive real number A (depending only on X,
$\Phi ^n(\alpha )\in V(K)$ is a union of finitely many arithmetic progressions along with a subset S with the property that there exists a positive real number A (depending only on X, 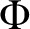 $\Phi $,
$\Phi $, 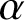 $\alpha $ and V) such that for each positive integer M,
$\alpha $ and V) such that for each positive integer M,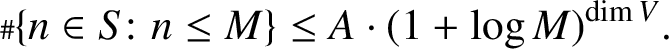
MSC classification
Information
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 104 , Issue 3 , December 2021 , pp. 381 - 390
- Copyright
- © 2021 Australian Mathematical Publishing Association Inc.
Footnotes
D. Ghioca and S. Saleh were partially supported by a Discovery Grant from NSERC, A. Ostafe by ARC Grants DP180100201 and DP200100355, and I. Shparlinski by ARC Grant DP200100355.
References
- 2
- Cited by


