Hostname: page-component-7dd5485656-7jgsp Total loading time: 0 Render date: 2025-10-31T05:40:11.961Z Has data issue: false hasContentIssue false
  • English
  • Français

NOTES ON THE K-RATIONAL DISTANCE PROBLEM

Part of: Arithmetic algebraic geometry Diophantine equations

Published online by Cambridge University Press:  01 December 2020

NGUYEN XUAN THO Open the ORCID record for NGUYEN XUAN THO [Opens in a new window]
NGUYEN XUAN THO*
Affiliation:
School of Applied Mathematics and Informatics, Hanoi University of Science and Technology, 1 Dai Co Viet Road, Hanoi, Vietnam
*
e-mail: tho.nguyenxuan1@hust.edu.vn
Get access Rights & Permissions [Opens in a new window]

Abstract

Let K be an algebraic number field. We investigate the K-rational distance problem and prove that there are infinitely many nonisomorphic cubic number fields and a number field of degree n for every 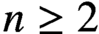$n\geq 2$ in which there is a point in the plane of a unit square at K-rational distances from the four vertices of the square.

Keywords

Diophantine equationsrational distance problemsolutions in number fields

MSC classification

Primary: 11D72: Equations in many variables
Secondary: 11G30: Curves of arbitrary genus or genus $ne 1$ over global fields

Information

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 104 , Issue 1 , August 2021 , pp. 40 - 44
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

The author is partially supported by the Vietnam National Foundation for Science and Technology Development (grant number 101.04-2019.314).

References

Berry, T. G., ‘Points at rational distance from corners of a unit square’, Ann. Sc. Norm. Super. Pisa Cl. Sci. (4) 17(4) (1990), 505–529.Google Scholar
Bremner, A., ‘On perfect $K$ -rational cuboids’, Bull. Aust. Math. Soc. 97 (2017), 26–32.CrossRefGoogle Scholar
Bremner, A. and Ulas, M., ‘Points at rational distances from the vertices of certain geometric objects’, J. Number Theory 158 (2016), 104–133.CrossRefGoogle Scholar
Faltings, G., ‘Endlichkeitssätze für abelsche Varietäten über Zahlkörpern’, Invent. Math. 73(3) (1983), 349–366.CrossRefGoogle Scholar
Guy, R. K., Unsolved Problems in Number Theory, 3rd edn (Springer, New York, 2003).Google Scholar
Prasolov, V. V., Polynomials (Springer, Berlin, Heidelberg, 2010).Google Scholar
Saunderson, N., The Elements of Algebra, Book 6 (Cambridge University Press, Cambridge, 1740), 429–431.Google Scholar