No CrossRef data available.
Article contents
ASKING QUESTIONS TO DETERMINE THE PRODUCT OF CIRCULARLY ARRANGED NUMBERS
Published online by Cambridge University Press: 19 April 2021
Abstract
Fix positive integers k and n with 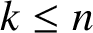 $k \leq n$. Numbers
$k \leq n$. Numbers 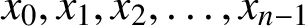 $x_0, x_1, x_2, \ldots , x_{n - 1}$, each equal to
$x_0, x_1, x_2, \ldots , x_{n - 1}$, each equal to 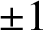 $\pm {1}$, are cyclically arranged (so that
$\pm {1}$, are cyclically arranged (so that 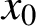 $x_0$ follows
$x_0$ follows 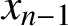 $x_{n - 1}$) in that order. The problem is to find the product
$x_{n - 1}$) in that order. The problem is to find the product 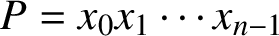 $P = x_0x_1 \cdots x_{n - 1}$ of all n numbers by asking the smallest number of questions of the type
$P = x_0x_1 \cdots x_{n - 1}$ of all n numbers by asking the smallest number of questions of the type 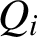 $Q_i$: what is
$Q_i$: what is 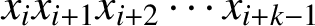 $x_ix_{i + 1}x_{i + 2} \cdots x_{i+ k -1}$? (where all the subscripts are read modulo n). This paper studies the problem and some of its generalisations.
$x_ix_{i + 1}x_{i + 2} \cdots x_{i+ k -1}$? (where all the subscripts are read modulo n). This paper studies the problem and some of its generalisations.
MSC classification
Primary:
05A17: Partitions of integers
Information
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 104 , Issue 2 , October 2021 , pp. 187 - 195
- Copyright
- © 2021 Australian Mathematical Publishing Association Inc.
References
Engels, A., Problem-Solving Strategies, Problem Books in Mathematics (Springer-Verlag, New York, 1998).Google Scholar
Godsil, C. and Royle, G. F.,
Algebraic Graph Theory, Graduate Texts in Mathematics, 207 (Springer-Verlag, New York, 2001).CrossRefGoogle Scholar
West, D. B.,
Introduction to Graph Theory, 2nd edn (Prentice Hall, Upper Saddle River, NJ, 2002).Google Scholar


