Refine search
Actions for selected content:
26203 results in Theoretical Physics and Mathematical Physics
Some investigations of gas discharges by means of an exploring electrode
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 5 / January 1927
- Published online by Cambridge University Press:
- 24 October 2008, pp. 531-541
- Print publication:
- January 1927
-
- Article
- Export citation
Note on the velocity of gas-reactions
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 4 / October 1926
- Published online by Cambridge University Press:
- 24 October 2008, pp. 438-449
- Print publication:
- October 1926
-
- Article
- Export citation
A mathematical theory of natural and artificial selection
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 4 / October 1926
- Published online by Cambridge University Press:
- 24 October 2008, pp. 363-372
- Print publication:
- October 1926
-
- Article
- Export citation
On Quantum Algebra
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 4 / October 1926
- Published online by Cambridge University Press:
- 24 October 2008, pp. 412-418
- Print publication:
- October 1926
-
- Article
- Export citation
Proceedings at the Meetings Held During the Session 1925–1926: Annual General Meeting
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 4 / October 1926
- Published online by Cambridge University Press:
- 24 October 2008, pp. 482-489
- Print publication:
- October 1926
-
- Article
- Export citation
An optical illusion due to contrast
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 4 / October 1926
- Published online by Cambridge University Press:
- 24 October 2008, pp. 419-421
- Print publication:
- October 1926
-
- Article
- Export citation
On the stability of copper catalysts produced by thermal decomposition
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 4 / October 1926
- Published online by Cambridge University Press:
- 24 October 2008, pp. 432-437
- Print publication:
- October 1926
-
- Article
- Export citation
On some resistance properties of a certain network containing inductances and capacities and their analogies in a vibrating mechanical system
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 4 / October 1926
- Published online by Cambridge University Press:
- 24 October 2008, pp. 391-402
- Print publication:
- October 1926
-
- Article
- Export citation
Note on the extension to higher space of a theorem of Wallace
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 4 / October 1926
- Published online by Cambridge University Press:
- 24 October 2008, pp. 361-362
- Print publication:
- October 1926
-
- Article
- Export citation
Note on the Petzval optical condition
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 4 / October 1926
- Published online by Cambridge University Press:
- 24 October 2008, pp. 461-464
- Print publication:
- October 1926
-
- Article
- Export citation
The elliptic products of Jacobi and the theory of linear congruences
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 4 / October 1926
- Published online by Cambridge University Press:
- 24 October 2008, pp. 337-355
- Print publication:
- October 1926
-
- Article
- Export citation
On compressional waves in two superposed layers
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 4 / October 1926
- Published online by Cambridge University Press:
- 24 October 2008, pp. 472-481
- Print publication:
- October 1926
-
- Article
- Export citation
On the Quantum Theory of the Problem of the Two Bodies
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 4 / October 1926
- Published online by Cambridge University Press:
- 24 October 2008, pp. 422-431
- Print publication:
- October 1926
-
- Article
- Export citation
The Polarisabilities of Atomic Cores
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 4 / October 1926
- Published online by Cambridge University Press:
- 24 October 2008, pp. 403-411
- Print publication:
- October 1926
-
- Article
- Export citation
PSP volume 23 issue 4 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 4 / October 1926
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
- Print publication:
- October 1926
-
- Article
-
- You have access
- Export citation
Statement of Accounts of the Cambridge Philosophical Society, from January 1, 1925, to December 31, 1925
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 4 / October 1926
- Published online by Cambridge University Press:
- 24 October 2008, pp. 490-491
- Print publication:
- October 1926
-
- Article
- Export citation
Improvements in the apparatus for measuring the velocity of very rapid chemical reactions
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 4 / October 1926
- Published online by Cambridge University Press:
- 24 October 2008, pp. 450-460
- Print publication:
- October 1926
-
- Article
- Export citation
On the descriptive form of Taylor's theorem
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 4 / October 1926
- Published online by Cambridge University Press:
- 24 October 2008, pp. 383-385
- Print publication:
- October 1926
-
- Article
- Export citation
The correspondence between lines in threefold space and points of a quadric fourfold in fivefold space, established by a geometrical construction
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 4 / October 1926
- Published online by Cambridge University Press:
- 24 October 2008, pp. 386-390
- Print publication:
- October 1926
-
- Article
- Export citation
Maxwell's Law, and the Absorption and Emission of Radiation
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 4 / October 1926
- Published online by Cambridge University Press:
- 24 October 2008, pp. 465-471
- Print publication:
- October 1926
-
- Article
- Export citation

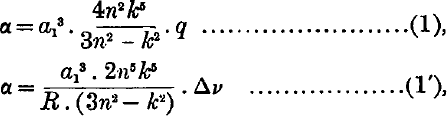
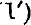 may be used, but for terms with large quantum defect (1) gives a higher degree of accuracy.
may be used, but for terms with large quantum defect (1) gives a higher degree of accuracy.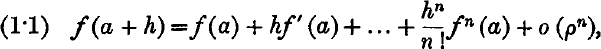
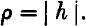
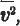 , is equal to its equipartition value, given by
, is equal to its equipartition value, given by 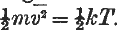 .
.