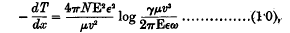Refine search
Actions for selected content:
26203 results in Theoretical Physics and Mathematical Physics
PSP volume 23 issue 6 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 6 / April 1927
- Published online by Cambridge University Press:
- 24 October 2008, p. b1
- Print publication:
- April 1927
-
- Article
-
- You have access
- Export citation
The Stopping Power of Hydrogen Atoms for α-Particles according to the New Quantum Theory
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 6 / April 1927
- Published online by Cambridge University Press:
- 24 October 2008, pp. 732-754
- Print publication:
- April 1927
-
- Article
- Export citation
An Experiment on the Stability of Superposed Streams of Fluid
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 6 / April 1927
- Published online by Cambridge University Press:
- 24 October 2008, pp. 730-731
- Print publication:
- April 1927
-
- Article
- Export citation
Contribution to the Theory of the Diffusion Pump
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 5 / January 1927
- Published online by Cambridge University Press:
- 24 October 2008, pp. 578-583
- Print publication:
- January 1927
-
- Article
- Export citation
PSP volume 23 issue 5 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 5 / January 1927
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
- Print publication:
- January 1927
-
- Article
-
- You have access
- Export citation
The absorption spectra of “saturated” and “unsaturated” organic substances
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 5 / January 1927
- Published online by Cambridge University Press:
- 24 October 2008, pp. 588-592
- Print publication:
- January 1927
-
- Article
- Export citation
The application of the method of the magnetic spectrum to the study of secondary electronic emission
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 5 / January 1927
- Published online by Cambridge University Press:
- 24 October 2008, pp. 523-530
- Print publication:
- January 1927
-
- Article
- Export citation
The calculation of atomic fields
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 5 / January 1927
- Published online by Cambridge University Press:
- 24 October 2008, pp. 542-548
- Print publication:
- January 1927
-
- Article
- Export citation
On the Figure of Pappus' Theorem
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 5 / January 1927
- Published online by Cambridge University Press:
- 24 October 2008, pp. 496-497
- Print publication:
- January 1927
-
- Article
- Export citation
The Tensile Deformation of Large Aluminium Crystals at Crystal Boundaries
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 5 / January 1927
- Published online by Cambridge University Press:
- 24 October 2008, pp. 549-560
- Print publication:
- January 1927
-
- Article
- Export citation
Note on the Effect of Alpha Particles on Paraffin
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 5 / January 1927
- Published online by Cambridge University Press:
- 24 October 2008, pp. 516-522
- Print publication:
- January 1927
-
- Article
- Export citation
Some Developments in the X-ray Analysis of Single-Crystals
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 5 / January 1927
- Published online by Cambridge University Press:
- 24 October 2008, pp. 561-577
- Print publication:
- January 1927
-
- Article
- Export citation
On a group of order 25920 and the projective transformations of a cubic surface
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 5 / January 1927
- Published online by Cambridge University Press:
- 24 October 2008, pp. 498-499
- Print publication:
- January 1927
-
- Article
- Export citation
Geodetic and Dynamical Principles, a comparison and connexion
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 5 / January 1927
- Published online by Cambridge University Press:
- 24 October 2008, pp. 493-495
- Print publication:
- January 1927
-
- Article
- Export citation
Surface adsorption and the velocity of chemical action at gas-solid interfaces
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 5 / January 1927
- Published online by Cambridge University Press:
- 24 October 2008, pp. 593-606
- Print publication:
- January 1927
-
- Article
- Export citation
The Compton Effect in Wave Mechanics
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 5 / January 1927
- Published online by Cambridge University Press:
- 24 October 2008, pp. 500-507
- Print publication:
- January 1927
-
- Article
- Export citation
PSP volume 23 issue 5 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 5 / January 1927
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
- Print publication:
- January 1927
-
- Article
-
- You have access
- Export citation
A mathematical theory of Natural and Artificial Selection
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 5 / January 1927
- Published online by Cambridge University Press:
- 24 October 2008, pp. 607-615
- Print publication:
- January 1927
-
- Article
- Export citation
On the polarisation of mercury lines emitted from a discharge tube in a magnetic field
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 5 / January 1927
- Published online by Cambridge University Press:
- 24 October 2008, pp. 508-515
- Print publication:
- January 1927
-
- Article
- Export citation
On the Addition of the Primary Aberrations
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 5 / January 1927
- Published online by Cambridge University Press:
- 24 October 2008, pp. 584-587
- Print publication:
- January 1927
-
- Article
- Export citation