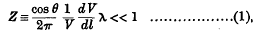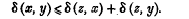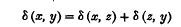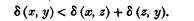Refine search
Actions for selected content:
26203 results in Theoretical Physics and Mathematical Physics
The production of characteristic X-rays by electronic impact
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 7 / July 1927
- Published online by Cambridge University Press:
- 24 October 2008, pp. 829-831
- Print publication:
- July 1927
-
- Article
- Export citation
A Mathematical Theory of Natural and Artificial Selection, Part V: Selection and Mutation
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 7 / July 1927
- Published online by Cambridge University Press:
- 24 October 2008, pp. 838-844
- Print publication:
- July 1927
-
- Article
- Export citation
PSP volume 23 issue 7 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 7 / July 1927
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
- Print publication:
- July 1927
-
- Article
-
- You have access
- Export citation
The total energy of binding of a heavy atom
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 7 / July 1927
- Published online by Cambridge University Press:
- 24 October 2008, pp. 794-799
- Print publication:
- July 1927
-
- Article
- Export citation
Some Measurements on the Absorption of X-Rays of Long Wave-length
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 7 / July 1927
- Published online by Cambridge University Press:
- 24 October 2008, pp. 783-793
- Print publication:
- July 1927
-
- Article
- Export citation
PSP volume 23 issue 7 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 7 / July 1927
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
- Print publication:
- July 1927
-
- Article
-
- You have access
- Export citation
On the Fifth Book of Euclid's Elements
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 7 / July 1927
- Published online by Cambridge University Press:
- 24 October 2008, pp. 779-782
- Print publication:
- July 1927
-
- Article
- Export citation
The Hall effect in Single Crystals of Iron
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 7 / July 1927
- Published online by Cambridge University Press:
- 24 October 2008, pp. 800-803
- Print publication:
- July 1927
-
- Article
- Export citation
A case of distinction between Fourier integrals and Fourier series
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 7 / July 1927
- Published online by Cambridge University Press:
- 24 October 2008, pp. 755-767
- Print publication:
- July 1927
-
- Article
- Export citation
What determines the Resistance and the Tilt of an Aeroplane?
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 6 / April 1927
- Published online by Cambridge University Press:
- 24 October 2008, pp. 617-630
- Print publication:
- April 1927
-
- Article
- Export citation
Notes on the theory of series (III): On the summability of the Fourier series of a nearly continuous function
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 6 / April 1927
- Published online by Cambridge University Press:
- 24 October 2008, pp. 681-684
- Print publication:
- April 1927
-
- Article
- Export citation
The evaluation of Gibbs' phase-integral for imperfect gases
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 6 / April 1927
- Published online by Cambridge University Press:
- 24 October 2008, pp. 685-697
- Print publication:
- April 1927
-
- Article
- Export citation
The Pedal (3, 2) Correspondence
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 6 / April 1927
- Published online by Cambridge University Press:
- 24 October 2008, pp. 631-652
- Print publication:
- April 1927
-
- Article
- Export citation
On Herschel's Condition and the Optical Cosine Law
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 6 / April 1927
- Published online by Cambridge University Press:
- 24 October 2008, pp. 703-712
- Print publication:
- April 1927
-
- Article
- Export citation
Note on Ramanujan's arithmetical function τ (n)
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 6 / April 1927
- Published online by Cambridge University Press:
- 24 October 2008, pp. 675-680
- Print publication:
- April 1927
-
- Article
- Export citation
PSP volume 23 issue 6 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 6 / April 1927
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
- Print publication:
- April 1927
-
- Article
-
- You have access
- Export citation
The effect of the orbital velocity of the electrons in heavy atoms on their stopping of α-particles
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 6 / April 1927
- Published online by Cambridge University Press:
- 24 October 2008, pp. 713-716
- Print publication:
- April 1927
-
- Article
- Export citation
The limits of classical scattering
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 6 / April 1927
- Published online by Cambridge University Press:
- 24 October 2008, pp. 698-702
- Print publication:
- April 1927
-
- Article
- Export citation
The Absolute Intensities of the γ-Rays of Radium B and Radium C
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 6 / April 1927
- Published online by Cambridge University Press:
- 24 October 2008, pp. 717-729
- Print publication:
- April 1927
-
- Article
- Export citation
Lines and Planes in a Metrical Space
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 6 / April 1927
- Published online by Cambridge University Press:
- 24 October 2008, pp. 653-674
- Print publication:
- April 1927
-
- Article
- Export citation
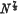 , where
, where 



 the sum of those of its odd divisors; and
the sum of those of its odd divisors; and