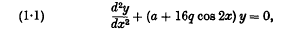Refine search
Actions for selected content:
26203 results in Theoretical Physics and Mathematical Physics
PSP volume 23 issue 4 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 4 / October 1926
- Published online by Cambridge University Press:
- 24 October 2008, p. b1
- Print publication:
- October 1926
-
- Article
-
- You have access
- Export citation
On Mellin's inversion formula
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 4 / October 1926
- Published online by Cambridge University Press:
- 24 October 2008, pp. 356-360
- Print publication:
- October 1926
-
- Article
- Export citation
The Summation of a Fourier Integral of Finite Type
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 4 / October 1926
- Published online by Cambridge University Press:
- 24 October 2008, pp. 373-382
- Print publication:
- October 1926
-
- Article
- Export citation
The Problem of Relativity in reference to several bodies
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 3 / July 1926
- Published online by Cambridge University Press:
- 24 October 2008, pp. 191-197
- Print publication:
- July 1926
-
- Article
- Export citation
On the higher singularities of plane algebraic curves
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 3 / July 1926
- Published online by Cambridge University Press:
- 24 October 2008, pp. 206-232
- Print publication:
- July 1926
-
- Article
- Export citation
A Theory of the Action of X-rays on living Cells
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 3 / July 1926
- Published online by Cambridge University Press:
- 24 October 2008, pp. 284-287
- Print publication:
- July 1926
-
- Article
- Export citation
An approximation to the motion of two rotating electrical doublets in a plane
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 3 / July 1926
- Published online by Cambridge University Press:
- 24 October 2008, pp. 269-283
- Print publication:
- July 1926
-
- Article
- Export citation
The (2, 1) Correspondence
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 3 / July 1926
- Published online by Cambridge University Press:
- 24 October 2008, pp. 233-261
- Print publication:
- July 1926
-
- Article
- Export citation
Integral Invariants of the Affine Field
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 3 / July 1926
- Published online by Cambridge University Press:
- 24 October 2008, pp. 262-268
- Print publication:
- July 1926
-
- Article
- Export citation
Some Relations between the Optical Spectra of Different Atoms of the same Electronic Structure. II. Aluminium-like and Copper-like Atoms
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 3 / July 1926
- Published online by Cambridge University Press:
- 24 October 2008, pp. 304-326
- Print publication:
- July 1926
-
- Article
- Export citation
On the Quantum Theory of Vibration-Rotation Bands
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 3 / July 1926
- Published online by Cambridge University Press:
- 24 October 2008, pp. 327-335
- Print publication:
- July 1926
-
- Article
- Export citation
Relativity in Connexion with Axial Rotation
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 3 / July 1926
- Published online by Cambridge University Press:
- 24 October 2008, pp. 198-202
- Print publication:
- July 1926
-
- Article
- Export citation
PSP volume 23 issue 3 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 3 / July 1926
- Published online by Cambridge University Press:
- 24 October 2008, p. f1
- Print publication:
- July 1926
-
- Article
-
- You have access
- Export citation
PSP volume 23 issue 3 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 3 / July 1926
- Published online by Cambridge University Press:
- 24 October 2008, p. b1
- Print publication:
- July 1926
-
- Article
-
- You have access
- Export citation
Sur la non-existence simultanée de deux fonctions de Mathieu
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 3 / July 1926
- Published online by Cambridge University Press:
- 24 October 2008, pp. 203-205
- Print publication:
- July 1926
-
- Article
- Export citation
On the Attenuation of Wireless Signals in Short Distance Overland Transmission
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 3 / July 1926
- Published online by Cambridge University Press:
- 24 October 2008, pp. 288-303
- Print publication:
- July 1926
-
- Article
- Export citation
PSP volume 23 issue 2 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 2 / April 1926
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
- Print publication:
- April 1926
-
- Article
-
- You have access
- Export citation
The General (m, n) Correspondence
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 2 / April 1926
- Published online by Cambridge University Press:
- 24 October 2008, pp. 109-119
- Print publication:
- April 1926
-
- Article
- Export citation
Oxidations on Charcoal
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 2 / April 1926
- Published online by Cambridge University Press:
- 24 October 2008, pp. 187-190
- Print publication:
- April 1926
-
- Article
- Export citation
The Behaviour of the Centres of Activity of Saturated Surfaces during the initial stages of Unimolecular Reactions
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 2 / April 1926
- Published online by Cambridge University Press:
- 24 October 2008, pp. 172-182
- Print publication:
- April 1926
-
- Article
- Export citation
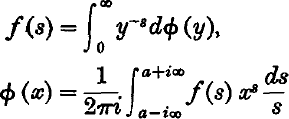
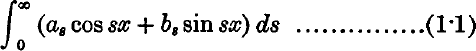

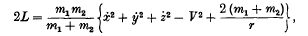
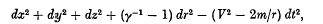
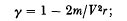
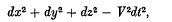

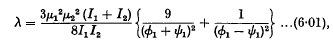
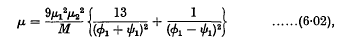
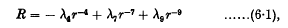
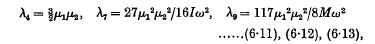
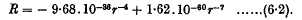
 and
and  . It is known that in order that such a function should be a scalar density it must be a homogeneous function, of degree ½
. It is known that in order that such a function should be a scalar density it must be a homogeneous function, of degree ½ , and this must of course be deducible from the equations found by the infinitesimal transformations. In view of the part which these equations may play, as “equations of energy,” etc., in purely affine field theories, it seems desirable that the connection should be explicitly shown, and this is done in § 3.
, and this must of course be deducible from the equations found by the infinitesimal transformations. In view of the part which these equations may play, as “equations of energy,” etc., in purely affine field theories, it seems desirable that the connection should be explicitly shown, and this is done in § 3. , where
, where  ; the weights of the corresponding states are 2
; the weights of the corresponding states are 2