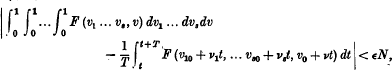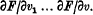Refine search
Actions for selected content:
26203 results in Theoretical Physics and Mathematical Physics
The second solution of the Mathieu equation
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 1 / February 1926
- Published online by Cambridge University Press:
- 24 October 2008, pp. 47-49
- Print publication:
- February 1926
-
- Article
- Export citation
PSP volume 23 issue 1 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 1 / February 1926
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
- Print publication:
- February 1926
-
- Article
-
- You have access
- Export citation
Periodic solutions of a linear differential equation of the second order with periodic coefficients
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 1 / February 1926
- Published online by Cambridge University Press:
- 24 October 2008, pp. 44-46
- Print publication:
- February 1926
-
- Article
- Export citation
On chains of two-two relations and the theory of elliptic functions
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 1 / February 1926
- Published online by Cambridge University Press:
- 24 October 2008, pp. 92-102
- Print publication:
- February 1926
-
- Article
- Export citation
PSP volume 23 issue 1 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 1 / February 1926
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f11
- Print publication:
- February 1926
-
- Article
-
- You have access
- Export citation
The quenching of resonance radiation and the breadths of absorption-lines
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 1 / February 1926
- Published online by Cambridge University Press:
- 24 October 2008, pp. 78-84
- Print publication:
- February 1926
-
- Article
- Export citation
A photographic method of determining the mobility of recoil atoms
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 1 / February 1926
- Published online by Cambridge University Press:
- 24 October 2008, pp. 73-77
- Print publication:
- February 1926
-
- Article
- Export citation
On the substitution of Wallis's Postulate of Similarity for Euclid's Postulate of Parallels
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 22 / Issue 6 / November 1925
- Published online by Cambridge University Press:
- 24 October 2008, pp. 964-969
- Print publication:
- November 1925
-
- Article
- Export citation
On Differentiation with respect to a Function
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 22 / Issue 6 / November 1925
- Published online by Cambridge University Press:
- 24 October 2008, pp. 924-934
- Print publication:
- November 1925
-
- Article
- Export citation
On the Theorem of Pappus
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 22 / Issue 6 / November 1925
- Published online by Cambridge University Press:
- 24 October 2008, pp. 919-923
- Print publication:
- November 1925
-
- Article
- Export citation
Doublet and Triplet Separations in Optical Spectra as Evidence whether Orbits penetrate into the Core
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 22 / Issue 6 / November 1925
- Published online by Cambridge University Press:
- 24 October 2008, pp. 904-918
- Print publication:
- November 1925
-
- Article
- Export citation
Notes on Optical Constants
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 22 / Issue 6 / November 1925
- Published online by Cambridge University Press:
- 24 October 2008, pp. 817-823
- Print publication:
- November 1925
-
- Article
- Export citation
Assemblies of Imperfect Gases by the method of Partition Functions
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 22 / Issue 6 / November 1925
- Published online by Cambridge University Press:
- 24 October 2008, pp. 861-885
- Print publication:
- November 1925
-
- Article
- Export citation
The Analysis of the β-Ray Spectrum due to the Natural L Radiation of Radium B
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 22 / Issue 6 / November 1925
- Published online by Cambridge University Press:
- 24 October 2008, pp. 838-843
- Print publication:
- November 1925
-
- Article
- Export citation
The Atomic Number of a Radioactive Element at the moment of emission of the γ-rays
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 22 / Issue 6 / November 1925
- Published online by Cambridge University Press:
- 24 October 2008, pp. 844-848
- Print publication:
- November 1925
-
- Article
- Export citation
The β-Ray Spectrum of the Natural L-Radiation from Radium B
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 22 / Issue 6 / November 1925
- Published online by Cambridge University Press:
- 24 October 2008, pp. 832-833
- Print publication:
- November 1925
-
- Article
- Export citation
The Lebesgue-Stieltjes Integral
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 22 / Issue 6 / November 1925
- Published online by Cambridge University Press:
- 24 October 2008, pp. 935-950
- Print publication:
- November 1925
-
- Article
- Export citation
PSP volume 22 issue 6 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 22 / Issue 6 / November 1925
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
- Print publication:
- November 1925
-
- Article
-
- You have access
- Export citation
Index to the Proceedings vol. XXII
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 22 / Issue 6 / November 1925
- Published online by Cambridge University Press:
- 24 October 2008, pp. 979-987
- Print publication:
- November 1925
-
- Article
- Export citation
An extended form of Kronecker's theorem with an application which shows that Burgers' theorem on adiabatic invariants is statistically true for an assembly
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 22 / Issue 6 / November 1925
- Published online by Cambridge University Press:
- 24 October 2008, pp. 886-903
- Print publication:
- November 1925
-
- Article
- Export citation


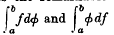 exists, so does the other, and their sum is equal to
exists, so does the other, and their sum is equal to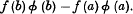
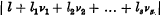 is greater than ηfor all sets of integers l
is greater than ηfor all sets of integers l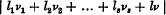
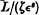 such that
such that