Refine search
Actions for selected content:
26203 results in Theoretical Physics and Mathematical Physics
Two sets of conditions for expansion in a Laurent's series
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 24 / Issue 1 / January 1928
- Published online by Cambridge University Press:
- 24 October 2008, pp. 38-47
- Print publication:
- January 1928
-
- Article
- Export citation
On the Lens Interferometer
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 24 / Issue 1 / January 1928
- Published online by Cambridge University Press:
- 24 October 2008, pp. 166-170
- Print publication:
- January 1928
-
- Article
- Export citation
A manometer for use with small Pitot tubes
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 24 / Issue 1 / January 1928
- Published online by Cambridge University Press:
- 24 October 2008, pp. 74-75
- Print publication:
- January 1928
-
- Article
- Export citation
PSP volume 24 issue 1 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 24 / Issue 1 / January 1928
- Published online by Cambridge University Press:
- 24 October 2008, p. f1
- Print publication:
- January 1928
-
- Article
-
- You have access
- Export citation
The Pure Archimedean Polytopes in Six and Seven Dimensions
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 24 / Issue 1 / January 1928
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1-9
- Print publication:
- January 1928
-
- Article
- Export citation
The Wave Mechanics of an Atom with a Non-Coulomb Central Field. Part II. Some Results and Discussion
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 24 / Issue 1 / January 1928
- Published online by Cambridge University Press:
- 24 October 2008, pp. 111-132
- Print publication:
- January 1928
-
- Article
- Export citation
The number of α-particles emitted by thorium C + C′
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 24 / Issue 1 / January 1928
- Published online by Cambridge University Press:
- 24 October 2008, pp. 133-138
- Print publication:
- January 1928
-
- Article
- Export citation
A condition for inverting the order of integration in a repeated integral
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 24 / Issue 1 / January 1928
- Published online by Cambridge University Press:
- 24 October 2008, pp. 35-37
- Print publication:
- January 1928
-
- Article
- Export citation
Note on the law that light-rays are the null geodesics of a gravitational field
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 24 / Issue 1 / January 1928
- Published online by Cambridge University Press:
- 24 October 2008, pp. 32-34
- Print publication:
- January 1928
-
- Article
- Export citation
The ionisation curve of an average α particle
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 24 / Issue 1 / January 1928
- Published online by Cambridge University Press:
- 24 October 2008, pp. 139-149
- Print publication:
- January 1928
-
- Article
- Export citation
The Classical limit of the space distribution law of a gas in a field of force
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 24 / Issue 1 / January 1928
- Published online by Cambridge University Press:
- 24 October 2008, pp. 76-79
- Print publication:
- January 1928
-
- Article
- Export citation
Notes on Spectrophotometry
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 8 / October 1927
- Published online by Cambridge University Press:
- 24 October 2008, pp. 959-969
- Print publication:
- October 1927
-
- Article
- Export citation
A Rapid Mercury Still
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 8 / October 1927
- Published online by Cambridge University Press:
- 24 October 2008, pp. 956-958
- Print publication:
- October 1927
-
- Article
- Export citation
The specific heat of carbon dioxide and the form of the CO2 molecule
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 8 / October 1927
- Published online by Cambridge University Press:
- 24 October 2008, pp. 890-900
- Print publication:
- October 1927
-
- Article
- Export citation
A Convenient Method of Distillation of the Alkali Metals
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 8 / October 1927
- Published online by Cambridge University Press:
- 24 October 2008, pp. 953-955
- Print publication:
- October 1927
-
- Article
- Export citation
The β-ray spectrum of Ra E
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 8 / October 1927
- Published online by Cambridge University Press:
- 24 October 2008, pp. 982-984
- Print publication:
- October 1927
-
- Article
- Export citation
The emission of radiation by a quadripole electric moment on the Quantum Mechanics
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 8 / October 1927
- Published online by Cambridge University Press:
- 24 October 2008, pp. 930-934
- Print publication:
- October 1927
-
- Article
- Export citation
On the generalizations of the theorems of Parseval and Riesz-Fischer
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 8 / October 1927
- Published online by Cambridge University Press:
- 24 October 2008, pp. 865-870
- Print publication:
- October 1927
-
- Article
- Export citation
Summation of the integral conjugate to the Fourier integral of finite type
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 8 / October 1927
- Published online by Cambridge University Press:
- 24 October 2008, pp. 871-881
- Print publication:
- October 1927
-
- Article
- Export citation
The Amount of Energy Emitted in the γ-Ray Form by Radium E
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 23 / Issue 8 / October 1927
- Published online by Cambridge University Press:
- 24 October 2008, pp. 935-941
- Print publication:
- October 1927
-
- Article
- Export citation
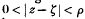 ; suppose that
; suppose that 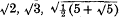 .
.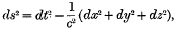 , the geodesics of the world are straight lines, and the null geodesics (i.e. the geodesics for which
, the geodesics of the world are straight lines, and the null geodesics (i.e. the geodesics for which