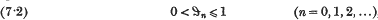Refine search
Actions for selected content:
26203 results in Theoretical Physics and Mathematical Physics
The Propagation of Electromagnetic Waves in a Refracting Medium in a Magnetic Field
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 27 / Issue 1 / January 1931
- Published online by Cambridge University Press:
- 24 October 2008, pp. 143-162
- Print publication:
- January 1931
-
- Article
- Export citation
The Diamagnetism of the Free Electron
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 27 / Issue 1 / January 1931
- Published online by Cambridge University Press:
- 24 October 2008, pp. 86-90
- Print publication:
- January 1931
-
- Article
- Export citation
On the Orthogonal Groups in Four Dimensions
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 27 / Issue 1 / January 1931
- Published online by Cambridge University Press:
- 24 October 2008, pp. 37-48
- Print publication:
- January 1931
-
- Article
- Export citation
In memory of the Rev. William Cecil, M.A., sometime Fellow of Magdalene College and Fellow of the Cambridge Philosophical Society
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 27 / Issue 1 / January 1931
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1-14
- Print publication:
- January 1931
-
- Article
- Export citation
PSP volume 27 issue 1 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 27 / Issue 1 / January 1931
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
- Print publication:
- January 1931
-
- Article
- Export citation
Note on Continuous Functionals
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 27 / Issue 1 / January 1931
- Published online by Cambridge University Press:
- 24 October 2008, pp. 49-56
- Print publication:
- January 1931
-
- Article
- Export citation
A Mathematical Theory of Natural Selection. Part VIII. Metastable Populations
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 27 / Issue 1 / January 1931
- Published online by Cambridge University Press:
- 24 October 2008, pp. 137-142
- Print publication:
- January 1931
-
- Article
- Export citation
The calculation of the van der Waal forces for hydrogen and helium at large inter-atomic distances
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 27 / Issue 1 / January 1931
- Published online by Cambridge University Press:
- 24 October 2008, pp. 66-72
- Print publication:
- January 1931
-
- Article
- Export citation
The Photoelectric Absorption of Gamma Rays
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 27 / Issue 1 / January 1931
- Published online by Cambridge University Press:
- 24 October 2008, pp. 103-112
- Print publication:
- January 1931
-
- Article
- Export citation
Note on some linear Diophantine inequalities
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 27 / Issue 1 / January 1931
- Published online by Cambridge University Press:
- 24 October 2008, pp. 24-25
- Print publication:
- January 1931
-
- Article
- Export citation
The Theory of the Scattering of Short X-rays by Molecular Hydrogen
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 27 / Issue 1 / January 1931
- Published online by Cambridge University Press:
- 24 October 2008, pp. 77-85
- Print publication:
- January 1931
-
- Article
- Export citation
The packing of certain sets of cubes
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 27 / Issue 1 / January 1931
- Published online by Cambridge University Press:
- 24 October 2008, pp. 57-65
- Print publication:
- January 1931
-
- Article
- Export citation
Note on the use of a thyratron with a Geiger counter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 27 / Issue 1 / January 1931
- Published online by Cambridge University Press:
- 24 October 2008, pp. 113-115
- Print publication:
- January 1931
-
- Article
- Export citation
Note on the Angular Scattering of Electrons in Gases
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 27 / Issue 1 / January 1931
- Published online by Cambridge University Press:
- 24 October 2008, pp. 73-76
- Print publication:
- January 1931
-
- Article
- Export citation
Preliminary Note on the Masses of the Electron, the Proton, and the Universe
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 27 / Issue 1 / January 1931
- Published online by Cambridge University Press:
- 24 October 2008, pp. 15-19
- Print publication:
- January 1931
-
- Article
- Export citation
Corrigenda
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 27 / Issue 1 / January 1931
- Published online by Cambridge University Press:
- 24 October 2008, p. 25
- Print publication:
- January 1931
-
- Article
-
- You have access
- Export citation
On the demonstration of electric lines of force, and a new method of measuring the electric moment of tourmaline
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 4 / October 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 491-495
- Print publication:
- October 1930
-
- Article
- Export citation
The number of contact primes of the canonical curve of genus p
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 4 / October 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 453-457
- Print publication:
- October 1930
-
- Article
- Export citation
On some series of functions
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 4 / October 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 458-474
- Print publication:
- October 1930
-
- Article
- Export citation
The Matrix Mechanics of the Spinning Electron
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 4 / October 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 496-506
- Print publication:
- October 1930
-
- Article
- Export citation
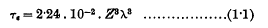
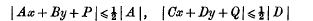
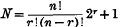 cubes. This paper discusses the possibility of completely filling space by means of the packing together of such sets of cubes.
cubes. This paper discusses the possibility of completely filling space by means of the packing together of such sets of cubes.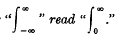

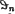 vary independently in the interval (0, 1). What we need is a definition of measure in the space of sequences
vary independently in the interval (0, 1). What we need is a definition of measure in the space of sequences 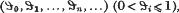 or, what is the same thing, in the space
or, what is the same thing, in the space