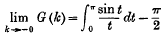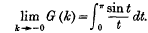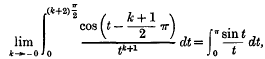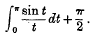Refine search
Actions for selected content:
26203 results in Theoretical Physics and Mathematical Physics
A portable apparatus for measuring the magnetic field strength in an electromagnetic wave
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 27 / Issue 3 / July 1931
- Published online by Cambridge University Press:
- 24 October 2008, pp. 481-489
- Print publication:
- July 1931
-
- Article
- Export citation
Involutions of pairs of points in three dimensions determined by cubic surfaces
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 27 / Issue 3 / July 1931
- Published online by Cambridge University Press:
- 24 October 2008, pp. 404-420
- Print publication:
- July 1931
-
- Article
- Export citation
Recombination of Ions in the Normal Arc
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 27 / Issue 3 / July 1931
- Published online by Cambridge University Press:
- 24 October 2008, pp. 421-429
- Print publication:
- July 1931
-
- Article
- Export citation
The triatomic hydrogen ion

-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 27 / Issue 3 / July 1931
- Published online by Cambridge University Press:
- 24 October 2008, pp. 451-459
- Print publication:
- July 1931
-
- Article
- Export citation
On the Determination of Plane Curves by means of Assigned Singularities
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 27 / Issue 3 / July 1931
- Published online by Cambridge University Press:
- 24 October 2008, pp. 291-305
- Print publication:
- July 1931
-
- Article
- Export citation
Some series and integrals involving associated Legendre functions (II)
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 27 / Issue 3 / July 1931
- Published online by Cambridge University Press:
- 24 October 2008, pp. 381-386
- Print publication:
- July 1931
-
- Article
- Export citation
Wave Functions of Many-Electron Atoms
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 27 / Issue 3 / July 1931
- Published online by Cambridge University Press:
- 24 October 2008, pp. 469-480
- Print publication:
- July 1931
-
- Article
- Export citation
Two Dynamical Applications of Quaternion Analysis
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 27 / Issue 3 / July 1931
- Published online by Cambridge University Press:
- 24 October 2008, pp. 391-392
- Print publication:
- July 1931
-
- Article
- Export citation
A series of rational loci with one apparent double point
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 27 / Issue 3 / July 1931
- Published online by Cambridge University Press:
- 24 October 2008, pp. 399-403
- Print publication:
- July 1931
-
- Article
- Export citation
A Method of Continuous Observation of the Equivalent Height of the Kennelly-Heaviside Layer
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 27 / Issue 3 / July 1931
- Published online by Cambridge University Press:
- 24 October 2008, pp. 445-450
- Print publication:
- July 1931
-
- Article
- Export citation
On many-valued Riemann-Stieltjes integration, II. Integration of bounded functions with respect to functions of bounded variation
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 27 / Issue 3 / July 1931
- Published online by Cambridge University Press:
- 24 October 2008, pp. 345-380
- Print publication:
- July 1931
-
- Article
- Export citation
Some advances towards a purely geometrical justification of the use of unreal elements in projective geometry
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 27 / Issue 3 / July 1931
- Published online by Cambridge University Press:
- 24 October 2008, pp. 306-325
- Print publication:
- July 1931
-
- Article
- Export citation
PSP volume 27 issue 3 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 27 / Issue 3 / July 1931
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
- Print publication:
- July 1931
-
- Article
- Export citation
Note on the Gibbs Phenomenon, II
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 27 / Issue 3 / July 1931
- Published online by Cambridge University Press:
- 24 October 2008, pp. 393-398
- Print publication:
- July 1931
-
- Article
- Export citation
On many-valued Riemann-Stieltjes integration
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 27 / Issue 3 / July 1931
- Published online by Cambridge University Press:
- 24 October 2008, pp. 326-344
- Print publication:
- July 1931
-
- Article
- Export citation
Concerning the success of the absorption method of investigating the high velocity limits of continuous β ray spectra
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 27 / Issue 3 / July 1931
- Published online by Cambridge University Press:
- 24 October 2008, pp. 430-444
- Print publication:
- July 1931
-
- Article
- Export citation
PSP volume 27 issue 3 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 27 / Issue 3 / July 1931
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
- Print publication:
- July 1931
-
- Article
- Export citation
On Abelian continuous groups
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 27 / Issue 3 / July 1931
- Published online by Cambridge University Press:
- 24 October 2008, pp. 387-390
- Print publication:
- July 1931
-
- Article
- Export citation
Some properties of line congruences
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 27 / Issue 2 / April 1931
- Published online by Cambridge University Press:
- 24 October 2008, pp. 190-200
- Print publication:
- April 1931
-
- Article
- Export citation
The Symmetric Derivative and its application to the Theory of Trigonometric Series
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 27 / Issue 2 / April 1931
- Published online by Cambridge University Press:
- 24 October 2008, pp. 163-173
- Print publication:
- April 1931
-
- Article
- Export citation

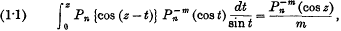
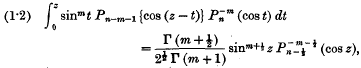
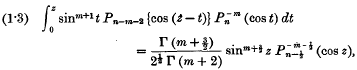
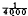 sec. are transmitted at regular
sec. are transmitted at regular 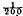 sec. intervals, and observed stroboscopically, together with their echoes, by means of a cathode ray oscillograph. Details of the transmitting and receiving apparatus are given. The rapid fluctuation in amplitude of the echoes is easily studied by this method.
sec. intervals, and observed stroboscopically, together with their echoes, by means of a cathode ray oscillograph. Details of the transmitting and receiving apparatus are given. The rapid fluctuation in amplitude of the echoes is easily studied by this method.