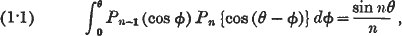Refine search
Actions for selected content:
26203 results in Theoretical Physics and Mathematical Physics
Statement of Accounts of the Cambridge Philosophical Society, From January 1, 1929, to December 31, 1929
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 4 / October 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 575-576
- Print publication:
- October 1930
-
- Article
- Export citation
Inverse Probability
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 4 / October 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 528-535
- Print publication:
- October 1930
-
- Article
- Export citation
Note on the sum of an oscillating series, II
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 4 / October 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 484-488
- Print publication:
- October 1930
-
- Article
- Export citation
The polarizability of the helium atom and the lithium ion
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 4 / October 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 542-555
- Print publication:
- October 1930
-
- Article
- Export citation
Some definite integrals involving Legendre functions
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 4 / October 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 475-479
- Print publication:
- October 1930
-
- Article
- Export citation
An unsuccessful attempt to influence the normal decay of a weak source of polonium
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 4 / October 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 538-541
- Print publication:
- October 1930
-
- Article
- Export citation
Surface Oscillations of Water in a Rotating Cylindrical Vessel
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 4 / October 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 446-452
- Print publication:
- October 1930
-
- Article
- Export citation
PSP volume 26 issue 4 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 4 / October 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b10
- Print publication:
- October 1930
-
- Article
-
- You have access
- Export citation
Wave forms, and a special problem
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 4 / October 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 438-445
- Print publication:
- October 1930
-
- Article
- Export citation
A percentile table of the relation between the true and the observed correlation coefficient from a sample of 4
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 4 / October 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 536-537
- Print publication:
- October 1930
-
- Article
- Export citation
Note on some linear Diophantine Inequalities
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 4 / October 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 489-490
- Print publication:
- October 1930
-
- Article
- Export citation
A Property of Continuous Arcs, II
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 4 / October 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 480-483
- Print publication:
- October 1930
-
- Article
- Export citation
Remarks on the scattering of electrons by atomic fields
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 4 / October 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 556-563
- Print publication:
- October 1930
-
- Article
- Export citation
PSP volume 26 issue 4 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 4 / October 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
- Print publication:
- October 1930
-
- Article
-
- You have access
- Export citation
On the strong summability of Fourier series
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 4 / October 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 429-437
- Print publication:
- October 1930
-
- Article
- Export citation
The triode oscillation generator and amplifier: limitations on sinoidal performance
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 4 / October 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 507-527
- Print publication:
- October 1930
-
- Article
- Export citation
Proceedings at the Meetings Held During the Session 1929–1930 Annual General Meeting
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 4 / October 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 564-574
- Print publication:
- October 1930
-
- Article
- Export citation
PSP volume 26 issue 3 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 3 / July 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
- Print publication:
- July 1930
-
- Article
-
- You have access
- Export citation
The Deformation of Soap Bubbles in Electric Fields
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 3 / July 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 421-428
- Print publication:
- July 1930
-
- Article
- Export citation
On the Annihilation of Electrons and Protons
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 3 / July 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 361-375
- Print publication:
- July 1930
-
- Article
- Export citation