Refine search
Actions for selected content:
26203 results in Theoretical Physics and Mathematical Physics
The theory of the extraction of electrons from metals by positive ions and metastable atoms
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 3 / July 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 386-401
- Print publication:
- July 1930
-
- Article
- Export citation
The Convergence of Singular Integrals
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 3 / July 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 312-322
- Print publication:
- July 1930
-
- Article
- Export citation
Note on the modified Heine-Borel Theorem
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 3 / July 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 334-336
- Print publication:
- July 1930
-
- Article
- Export citation
On some series of functions, (1)
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 3 / July 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 337-357
- Print publication:
- July 1930
-
- Article
- Export citation
Note on Exchange Phenomena in the Thomas Atom
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 3 / July 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 376-385
- Print publication:
- July 1930
-
- Article
-
- You have access
- Export citation
Multiple tangents to forms in four dimensions
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 3 / July 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 285-304
- Print publication:
- July 1930
-
- Article
- Export citation
A Phase Diagram for Unimolecular Films
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 3 / July 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 419-420
- Print publication:
- July 1930
-
- Article
- Export citation
The quarto-quartic transformation of four-dimensional space associated, with certain protectively generated loci
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 3 / July 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 323-333
- Print publication:
- July 1930
-
- Article
- Export citation
The Real Representation of the Commutator S−1 T−1 ST in Four Dimensions
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 3 / July 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 305-311
- Print publication:
- July 1930
-
- Article
- Export citation
Two Formulae for Space Curves
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 3 / July 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 358-360
- Print publication:
- July 1930
-
- Article
- Export citation
PSP volume 26 issue 3 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 3 / July 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
- Print publication:
- July 1930
-
- Article
-
- You have access
- Export citation
Rotational Specific Heat and Rotational Entropy of Simple Gases at Moderate Temperatures
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 3 / July 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 402-418
- Print publication:
- July 1930
-
- Article
- Export citation
On the Cesàro summability of Fourier series and Allied series
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 2 / April 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 173-203
- Print publication:
- April 1930
-
- Article
- Export citation
Note on the Gibbs Phenomenon
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 2 / April 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 158-169
- Print publication:
- April 1930
-
- Article
- Export citation
The law of stifling of sound by curtains or cushions
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 2 / April 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 231-235
- Print publication:
- April 1930
-
- Article
- Export citation
The Draining of a Vertical Plate
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 2 / April 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 204-205
- Print publication:
- April 1930
-
- Article
- Export citation
PSP volume 26 issue 2 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 2 / April 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
- Print publication:
- April 1930
-
- Article
-
- You have access
- Export citation
Continued Fractions in Several Dimensions
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 2 / April 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 127-144
- Print publication:
- April 1930
-
- Article
- Export citation
The Absorption of β-Rays
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 2 / April 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 252-257
- Print publication:
- April 1930
-
- Article
- Export citation
A mathematical theory of natural and artificial selection. (Part VI, Isolation.)
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 2 / April 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 220-230
- Print publication:
- April 1930
-
- Article
- Export citation


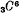 . A similar transformation, in space of any number of dimensions, has been described analytically in a note by Godeaux; and most of our work in the present paper extends to the general case. The case of four dimensions is studied here as being less abstract, and more easily susceptible of geometrical treatment; in the general case it is less simple to dispense completely with algebraical methods. We shall see that the various loci which arise in the course of the work are already well known.
. A similar transformation, in space of any number of dimensions, has been described analytically in a note by Godeaux; and most of our work in the present paper extends to the general case. The case of four dimensions is studied here as being less abstract, and more easily susceptible of geometrical treatment; in the general case it is less simple to dispense completely with algebraical methods. We shall see that the various loci which arise in the course of the work are already well known.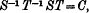
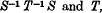
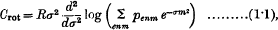
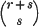 denote
denote