Refine search
Actions for selected content:
26203 results in Theoretical Physics and Mathematical Physics
A transformation of a formula of Sommerfeld
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 2 / April 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 123-126
- Print publication:
- April 1930
-
- Article
- Export citation
On the remarkable quadrics of a space cubic curve
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 2 / April 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 206-219
- Print publication:
- April 1930
-
- Article
- Export citation
The Instability of a Compressible Fluid heated below
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 2 / April 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 170-172
- Print publication:
- April 1930
-
- Article
- Export citation
On a Type of Automatically Interrupted Triode Oscillations
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 2 / April 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 236-251
- Print publication:
- April 1930
-
- Article
- Export citation
Note on the sum of an oscillating series
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 2 / April 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 152-157
- Print publication:
- April 1930
-
- Article
- Export citation
PSP volume 26 issue 2 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 2 / April 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
- Print publication:
- April 1930
-
- Article
-
- You have access
- Export citation
A New Method of Examination of Surface Films
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 2 / April 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 273-277
- Print publication:
- April 1930
-
- Article
- Export citation
The Remainders in the Asymptotic Expansions of Certain Bessel Functions
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 2 / April 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 145-151
- Print publication:
- April 1930
-
- Article
- Export citation
A Microcalorimeter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 2 / April 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 278-284
- Print publication:
- April 1930
-
- Article
- Export citation
The Added Mass of Prisms Floating in Water
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 2 / April 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 258-272
- Print publication:
- April 1930
-
- Article
- Export citation
Enumerative Formulae for Surfaces
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 1 / January 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 43-71
- Print publication:
- January 1930
-
- Article
- Export citation
An attempt to detect an Electric Moment in a Light Quantum
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 1 / January 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 117-121
- Print publication:
- January 1930
-
- Article
- Export citation
The Thermodynamics of an Elastic Solid
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 1 / January 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 101-106
- Print publication:
- January 1930
-
- Article
- Export citation
Some series of squares of Bessel functions
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 1 / January 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 82-87
- Print publication:
- January 1930
-
- Article
- Export citation
PSP volume 26 issue 1 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 1 / January 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
- Print publication:
- January 1930
-
- Article
-
- You have access
- Export citation
PSP volume 26 issue 1 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 1 / January 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
- Print publication:
- January 1930
-
- Article
-
- You have access
- Export citation
On the Equation of State of an Ionised Gas
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 1 / January 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 107-114
- Print publication:
- January 1930
-
- Article
- Export citation
On the existence of non-combining groups of wave-functions, and on the uniqueness of the solutions of certain wave equations
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 1 / January 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 99-100
- Print publication:
- January 1930
-
- Article
- Export citation
Representation of the planes of five-dimensional space
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 1 / January 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 72-81
- Print publication:
- January 1930
-
- Article
- Export citation
Concerning some Solutions of the Boundary Layer Equations in Hydrodynamics
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 26 / Issue 1 / January 1930
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1-30
- Print publication:
- January 1930
-
- Article
- Export citation
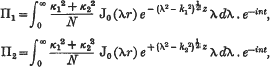
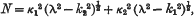
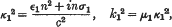
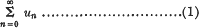
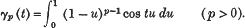
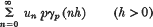
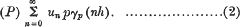
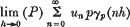
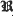 , p) of the series (1).
, p) of the series (1).