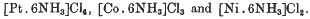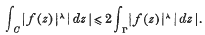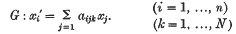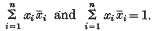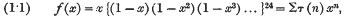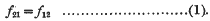Refine search
Actions for selected content:
26203 results in Theoretical Physics and Mathematical Physics
On the Phragmén-Lindelöf Principle
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 3 / July 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 265-267
- Print publication:
- July 1929
-
- Article
- Export citation
On Ramanujan's Arithmetical Function Σr, s(n)
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 3 / July 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 255-264
- Print publication:
- July 1929
-
- Article
- Export citation
An Analysis of Triode Valve Rectification
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 3 / July 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 355-367
- Print publication:
- July 1929
-
- Article
- Export citation
On the Transport of Sediments by Streams
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 3 / July 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 272-276
- Print publication:
- July 1929
-
- Article
- Export citation
An Approximate Method of Determining the High-Velocity Limits of Continuous β-ray Spectra
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 3 / July 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 331-339
- Print publication:
- July 1929
-
- Article
- Export citation
PSP volume 25 issue 3 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 3 / July 1929
- Published online by Cambridge University Press:
- 24 October 2008, p. f1
- Print publication:
- July 1929
-
- Article
-
- You have access
- Export citation
Double Row of Vortices with Arbitrary Stagger
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 2 / April 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 132-138
- Print publication:
- April 1929
-
- Article
- Export citation
Secondary Electron Emission from Solid Metal Surfaces
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 2 / April 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 237-254
- Print publication:
- April 1929
-
- Article
- Export citation
Configuration of Quadrivalent Atoms
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 2 / April 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 219-221
- Print publication:
- April 1929
-
- Article
- Export citation
Thermionic Emission through double layers
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 2 / April 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 175-185
- Print publication:
- April 1929
-
- Article
- Export citation
The Mobility Distribution and Rate of Formation of Negative Ions in Air
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 2 / April 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 205-218
- Print publication:
- April 1929
-
- Article
- Export citation
The Distribution of Charge and Current in an Atom consisting of many Electrons obeying Dirac's equations
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 2 / April 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 225-236
- Print publication:
- April 1929
-
- Article
- Export citation
Some further results concerning the integrals of moduli of regular functions along curves of certain types
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 2 / April 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 139-144
- Print publication:
- April 1929
-
- Article
- Export citation
A Geometrical Study of the Alternating and Symmetric Groups
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 2 / April 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 168-174
- Print publication:
- April 1929
-
- Article
- Export citation
A note on Ramanujan's arithmetical function τ(n)
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 2 / April 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 121-129
- Print publication:
- April 1929
-
- Article
- Export citation
Energy Relations in Artificial Disintegration
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 2 / April 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 186-192
- Print publication:
- April 1929
-
- Article
- Export citation
PSP volume 25 issue 2 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 2 / April 1929
- Published online by Cambridge University Press:
- 24 October 2008, p. b1
- Print publication:
- April 1929
-
- Article
-
- You have access
- Export citation
On Certain Loci of Three Dimensions Representable on Ordinary Space by means of Cubic Surfaces, and the Cremona Transformations for Ordinary Space obtained by Projection of such Loci
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 2 / April 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 145-167
- Print publication:
- April 1929
-
- Article
- Export citation
Note on the Number of High Velocity β-rays
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 2 / April 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 222-224
- Print publication:
- April 1929
-
- Article
- Export citation
An analogy for beams of particles of a reciprocal optical theorem due to Helmholtz
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 2 / April 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 193-197
- Print publication:
- April 1929
-
- Article
- Export citation
 ;
;
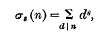
 , where ζ(
, where ζ(

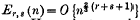 , whenever
, whenever 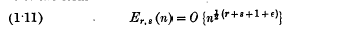
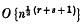 . He further conjectures that
. He further conjectures that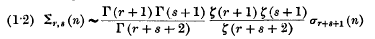
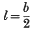 the system is the unsymmetrical double row.
the system is the unsymmetrical double row.