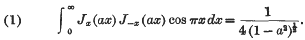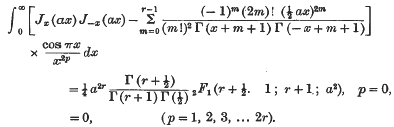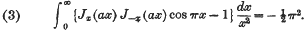Refine search
Actions for selected content:
26203 results in Theoretical Physics and Mathematical Physics
The distribution of range of the α particles from radium C′ and thorium C′
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 2 / April 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 198-204
- Print publication:
- April 1929
-
- Article
- Export citation
PSP volume 25 issue 2 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 2 / April 1929
- Published online by Cambridge University Press:
- 24 October 2008, p. f1
- Print publication:
- April 1929
-
- Article
-
- You have access
- Export citation
A Note on Some Integrals Involving Bessel Functions
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 2 / April 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 130-131
- Print publication:
- April 1929
-
- Article
- Export citation
On the transverse circulation in streams
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 1 / January 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 20-25
- Print publication:
- January 1929
-
- Article
- Export citation
PSP volume 25 issue 1 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 1 / January 1929
- Published online by Cambridge University Press:
- 24 October 2008, p. f1
- Print publication:
- January 1929
-
- Article
-
- You have access
- Export citation
The Passage of β-rays through matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 1 / January 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 50-61
- Print publication:
- January 1929
-
- Article
- Export citation
The classification of orbits
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 1 / January 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1-19
- Print publication:
- January 1929
-
- Article
- Export citation
Cayley's problem of seven lines on a quartic surface
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 1 / January 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 31-38
- Print publication:
- January 1929
-
- Article
- Export citation
The basis of statistical quantum mechanics
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 1 / January 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 62-66
- Print publication:
- January 1929
-
- Article
- Export citation
A note on Bateman's expansion in Bessel functions
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 1 / January 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 48-49
- Print publication:
- January 1929
-
- Article
- Export citation
The propagation of electromagnetic waves in a stratified medium
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 1 / January 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 97-120
- Print publication:
- January 1929
-
- Article
- Export citation
Current measurement with a Compton quadrant electrometer
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 1 / January 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 67-74
- Print publication:
- January 1929
-
- Article
- Export citation
The dispersion electrons of lithium
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 1 / January 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 75-96
- Print publication:
- January 1929
-
- Article
- Export citation
On Young's criteria for the convergence of Fourier series and their conjugates
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 1 / January 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 26-30
- Print publication:
- January 1929
-
- Article
- Export citation
On the number of planes in hyperspace which satisfy a certain set of conditions
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 1 / January 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 42-47
- Print publication:
- January 1929
-
- Article
- Export citation
PSP volume 25 issue 1 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 1 / January 1929
- Published online by Cambridge University Press:
- 24 October 2008, p. b1
- Print publication:
- January 1929
-
- Article
-
- You have access
- Export citation
Coincidence formulae in geometry
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 1 / January 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 39-41
- Print publication:
- January 1929
-
- Article
- Export citation
PSP volume 24 issue 4 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 24 / Issue 4 / October 1928
- Published online by Cambridge University Press:
- 24 October 2008, p. f1
- Print publication:
- October 1928
-
- Article
-
- You have access
- Export citation
Some Applications of Fourier series in the Analytic Theory of Numbers
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 24 / Issue 4 / October 1928
- Published online by Cambridge University Press:
- 24 October 2008, pp. 585-596
- Print publication:
- October 1928
-
- Article
- Export citation
On Tidal Waves in Canals having Sinuous Banks
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 24 / Issue 4 / October 1928
- Published online by Cambridge University Press:
- 24 October 2008, pp. 567-577
- Print publication:
- October 1928
-
- Article
- Export citation