Refine search
Actions for selected content:
26203 results in Theoretical Physics and Mathematical Physics
PSP volume 25 issue 4 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 4 / October 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b8
- Print publication:
- October 1929
-
- Article
-
- You have access
- Export citation
The Upper Limits of Energy in the β-ray Spectra of Actinium B and Actinium C″
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 4 / October 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 514-521
- Print publication:
- October 1929
-
- Article
- Export citation
Some Particular Line-systems of Higher Space
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 4 / October 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 436-444
- Print publication:
- October 1929
-
- Article
- Export citation
Poisson's Summation Formula in several Variables and some Applications to the Theory of Numbers
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 4 / October 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 412-420
- Print publication:
- October 1929
-
- Article
- Export citation
Motion of a Sphere in a Viscous Fluid
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 4 / October 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 369-383
- Print publication:
- October 1929
-
- Article
- Export citation
On the Convergence of a certain Multiple Series
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 4 / October 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 407-409
- Print publication:
- October 1929
-
- Article
- Export citation
Extension of a Geometrical Porism and other Theorems
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 4 / October 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 421-432
- Print publication:
- October 1929
-
- Article
- Export citation
The Wave Mechanics of an Atom with a Non-Coulomb Central Field. Part IV. Further Results relating to Terms of the Optical Spectrum
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 3 / July 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 310-314
- Print publication:
- July 1929
-
- Article
- Export citation
Some Calculations relevant to the Quantum Defect in the Extended Ritz Formula
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 3 / July 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 315-322
- Print publication:
- July 1929
-
- Article
- Export citation
The Dispersion Electrons in the One-Electron Problem
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 3 / July 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 323-330
- Print publication:
- July 1929
-
- Article
- Export citation
The Second Mean Value Theorem in the Integral Calculus
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 3 / July 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 282-284
- Print publication:
- July 1929
-
- Article
- Export citation
PSP volume 25 issue 3 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 3 / July 1929
- Published online by Cambridge University Press:
- 24 October 2008, p. b1
- Print publication:
- July 1929
-
- Article
-
- You have access
- Export citation
Systems of Double Rows of Line Vortices in a Channel of Finite Breadth where the Axis of the Row is Parallel to the Axis of the Channel
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 3 / July 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 277-281
- Print publication:
- July 1929
-
- Article
- Export citation
Jacobian surfaces of quadrics in four dimensions
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 3 / July 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 268-271
- Print publication:
- July 1929
-
- Article
- Export citation
On the Obliquity Function to be used in the Approximate Theory of Diffraction
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 3 / July 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 289-303
- Print publication:
- July 1929
-
- Article
- Export citation
Note on the Condensation of Radioactive Substances on Solid Surfaces
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 3 / July 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 344-346
- Print publication:
- July 1929
-
- Article
- Export citation
The Quantum Theory of electronic scattering by Helium
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 3 / July 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 304-309
- Print publication:
- July 1929
-
- Article
- Export citation
A Proof of Miquel's Theorem by Involutions in the Argand Diagram
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 3 / July 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 285-288
- Print publication:
- July 1929
-
- Article
- Export citation
Layers of Caesium, and Nitrogen on Tungsten
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 3 / July 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 347-354
- Print publication:
- July 1929
-
- Article
- Export citation
A New Electroscope
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 25 / Issue 3 / July 1929
- Published online by Cambridge University Press:
- 24 October 2008, pp. 340-343
- Print publication:
- July 1929
-
- Article
- Export citation
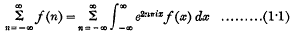
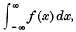 ,
, 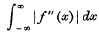 converge.
converge.

