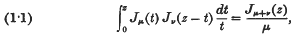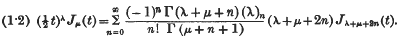Refine search
Actions for selected content:
26203 results in Theoretical Physics and Mathematical Physics
On the influence of radiative forces on the scattering of electrons
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 27 / Issue 2 / April 1931
- Published online by Cambridge University Press:
- 24 October 2008, pp. 255-267
- Print publication:
- April 1931
-
- Article
- Export citation
A note on Ferromagnetism
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 27 / Issue 2 / April 1931
- Published online by Cambridge University Press:
- 24 October 2008, pp. 280-289
- Print publication:
- April 1931
-
- Article
- Export citation
The Densities of the Regular Polytopes
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 27 / Issue 2 / April 1931
- Published online by Cambridge University Press:
- 24 October 2008, pp. 201-211
- Print publication:
- April 1931
-
- Article
- Export citation
Some series and integrals involving associated Legendre functions
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 27 / Issue 2 / April 1931
- Published online by Cambridge University Press:
- 24 October 2008, pp. 184-189
- Print publication:
- April 1931
-
- Article
- Export citation
Note on the Interpretation of the Density Matrix in the Many-Electron Problem
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 27 / Issue 2 / April 1931
- Published online by Cambridge University Press:
- 24 October 2008, pp. 240-243
- Print publication:
- April 1931
-
- Article
- Export citation
The groups of symmetries of the regular polytopes
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 27 / Issue 2 / April 1931
- Published online by Cambridge University Press:
- 24 October 2008, pp. 212-231
- Print publication:
- April 1931
-
- Article
- Export citation
PSP volume 27 issue 2 Cover and Back matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 27 / Issue 2 / April 1931
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
- Print publication:
- April 1931
-
- Article
-
- You have access
- Export citation
A Theoretical Discussion of the Electrical Properties of the Soil
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 27 / Issue 2 / April 1931
- Published online by Cambridge University Press:
- 24 October 2008, pp. 268-276
- Print publication:
- April 1931
-
- Article
- Export citation
On the desorption of gases from the walls of a closed system in which the pressure is independently changing
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 27 / Issue 2 / April 1931
- Published online by Cambridge University Press:
- 24 October 2008, pp. 250-254
- Print publication:
- April 1931
-
- Article
- Export citation
Note on the operability of a synchronous motor at the end of a transmission line
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 27 / Issue 2 / April 1931
- Published online by Cambridge University Press:
- 24 October 2008, pp. 244-249
- Print publication:
- April 1931
-
- Article
- Export citation
On the combinatory scheme of analysis
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 27 / Issue 2 / April 1931
- Published online by Cambridge University Press:
- 24 October 2008, pp. 232-239
- Print publication:
- April 1931
-
- Article
- Export citation
On Summable Trigonometric Integrals
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 27 / Issue 2 / April 1931
- Published online by Cambridge University Press:
- 24 October 2008, pp. 174-183
- Print publication:
- April 1931
-
- Article
- Export citation
The weak lines in the natural β-ray spectrum of radium C
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 27 / Issue 2 / April 1931
- Published online by Cambridge University Press:
- 24 October 2008, pp. 277-279
- Print publication:
- April 1931
-
- Article
- Export citation
PSP volume 27 issue 2 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 27 / Issue 2 / April 1931
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
- Print publication:
- April 1931
-
- Article
-
- You have access
- Export citation
A Mathematical Theory of Natural and Artificial Selection. Part VII. Selection intensity as a function of mortality rate
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 27 / Issue 1 / January 1931
- Published online by Cambridge University Press:
- 24 October 2008, pp. 131-136
- Print publication:
- January 1931
-
- Article
- Export citation
On elliptic quartic curves with assigned points and chords
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 27 / Issue 1 / January 1931
- Published online by Cambridge University Press:
- 24 October 2008, pp. 20-23
- Print publication:
- January 1931
-
- Article
- Export citation
On the Rotation of Dielectrics in Electrostatic Fields and Related Phenomena
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 27 / Issue 1 / January 1931
- Published online by Cambridge University Press:
- 24 October 2008, pp. 91-102
- Print publication:
- January 1931
-
- Article
- Export citation
The Capture of Electrons by α-Particles
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 27 / Issue 1 / January 1931
- Published online by Cambridge University Press:
- 24 October 2008, pp. 116-130
- Print publication:
- January 1931
-
- Article
- Export citation
On the Operational Solution of Linear Finite Difference Equations
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 27 / Issue 1 / January 1931
- Published online by Cambridge University Press:
- 24 October 2008, pp. 26-36
- Print publication:
- January 1931
-
- Article
- Export citation
PSP volume 27 issue 1 Cover and Front matter
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 27 / Issue 1 / January 1931
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
- Print publication:
- January 1931
-
- Article
- Export citation