When a mass of air, saturated with water vapour at room temperature θ1, is expanded adiabatically, the temperature falls to a lower temperature θ2. In general the resulting density of water vapour is greater than the equilibrium value at the temperature θ2 and condensation commences. This condensation causes heating of the gas and the temperature rises until finally at some temperature θ3 the density of uncondensed vapour is equal to the equilibrium vapour density at θ3. (θ1 > θ3 > θ2.) Condensation then ceases and the air rises slowly to room temperature by heat conduction through the walls of the apparatus.

The problem of statistical investigation is the description of a population, or Kollektiv, of which a sample has been observed. At best we can only state the probability that certain parameters of this population lie within assigned limits, i.e. specify their probability density. It has been shown, e.g. by von Mises(1), that this is only possible if we know the probability distribution of the parameter before the sample is taken. Bayes' theorem is based on the assumption that all values of the parameter in the neighbourhood of that observed are equally probable a priori. It is the purpose of this paper to examine what more reasonable assumption may be made, and how it will affect the estimate based on the observed sample.

1. The problem of finding the number of space cubic curves which pass through p given points and have 6 – p given lines as chords has been solved by several different methods. The similar problem, in space of four dimensions, of the number of rational quartic curves which pass through p given points and have 7 – p given trisecant planes has been solved for p > 1 by F. P. White and for p = 1 by J. A. Todd. In a recent paper I discussed a similar problem for elliptic quartic curves. My present object is to apply the method of that paper to the problems mentioned above and to obtain two other sets of numbers which I believe to be new. They are (1) the number of rational normal quartic curves which have three assigned chords, pass through p assigned points, and have 3 – p assigned trisecant planes; (2) the number of curves of intersection of three quadrics in [4] which have a suitable number of assigned points and chords. The evaluation of Schubert symbols which occur in the work is done by means of a formula due to Giambelli‖. This formula is stated in a more simple form in a note at the end of this paper (7).

The magnetisation of a single crystal of a ferromagnetic substance is accompanied by a distortion of the crystal which depends on the intensity and direction of magnetisation. Webster has shown that the magnetostriction in unsaturated states may be accounted for in an entirely satisfactory manner by making the assumption (for which the evidence is entirely convincing) that at ordinary temperatures an apparently unmagnetised crystal consists of small regions magnetised to saturation in various directions, so as to give no resultant magnetisation to the whole crystal, and that these regions possess natural directions of easy magnetisation.

1. It is possible to treat the excitation of an atom by an α-particle in two ways; we may either solve the Schrödinger equation for the system consisting of the α-particle and the atom, or we may, on account of the great mass of the α-particle, treat it as a moving centre of force, and solve the Schrödinger equation for the electrons in the field of the α-particle and nucleus, If the α-particle has velocity υ greater than the orbital velocities of the electrons, it is possible to obtain approximate formulae for the excitation probabilities by both methods; in the former case by the well known Born method, and in the latter case by a method first used in this connection by Gaunt*, and which is essentially the same as the method of variation of constants. The two methods give formally very different formulae for the excitation probabilities; it is the purpose of this paper to show that they are in fact identical if the ratio of the mass of the electron to that of the α-particle be considered vanishingly small.

A mechanical method of integrating a second-order differential equation, with any boundary conditions, is described and its applications are discussed.

In a recent paper Mr W. G. Welchman has devised an extremely simple method for determining the number of elliptic quartic curves in space which pass through p given points and have 8–p assigned lines as chords. In the present note this method will be applied, with certain necessary extensions, to some cases in which the curves are subject to the condition of meeting certain lines in one point only, in addition to conditions of the previous type. The method in principle is perfectly straightforward, but circumstances arise which make its application somewhat limited.

1. It has been shown, in a well-known paper by Born and Oppenheimer, that in evaluating the energy levels of a molecule, the nuclei may be treated as fixed, or slowly vibrating, centres of force. If M be the average mass of the nuclei, and m the mass of an electron, the error involved in doing this is of order of magnitude (m/M)½. The possibility therefore of treating the nuclei as fixed depends on their great mass, compared with that of the electron.

If a receiving aerial is placed in the field of a wave produced by a distant transmitter, currents are induced in the receiving aerial and these dissipate energy in the ohmic resistances of the aerial. This energy may be thought of as being absorbed directly from the incident wave, but this viewpoint gives no insight into the mechanism by which the absorption takes place. In this paper the following alternative way of regarding the phenomenon is considered. The currents induced in the aerial cause it to re-radiate a secondary wave. The electric and magnetic fields of this secondary wave combine with those of the unabsorbed incident wave to give resultant fields which have, in general, a direction different from those of the incident wave. These resultant fields give rise to energy flows which are different from those in the incident wave, both in magnitude and direction. In this way a flow of energy into the aerial is produced, by the superposition of the incident and the re-radiated fields. It is important to notice that if this viewpoint is adopted we must add the secondary re-radiated wave to the unabsorbed main wave, the addition, in itself, producing the requisite absorption.

The theory of the intersection-complex Ch · Ck, due originally to Veblen, Weyl, Alexander and Lefschetz, has recently been extended by Flexner to cover intersections on a “topological n-manifold” (locally Cartesian n-space) in the case h + k = n. In his theory the whole of Lefschetz's work for ordinary simplicial manifolds is presupposed, including the rather difficult approximations. The object of the present paper is to provide a combinatory theory of the general intersection, (h + k ≥ n), which would serve equally well as a basis for Flexner's work, and avoids the wasteful process of using two independent approximations.

1. In a note in these Proceedings, Mr S. Verblunsky proves the following result:

Theorem A. Let C be a continuous arc joining the points (x1, y0) and (x2, y0), where x2 > x1. Suppose that C does not cross the line y = y0. Then, given any positive h < x2 − x1, there is α yh such that some two points (ξ1, yh), (ξ2, yh), in which y = yh cuts C, satisfy the relation ξ2 − ξ1 = h.

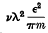Larmor has shown that if the upper atmosphere contains electrons (charge ε, mass m, density ν) and if collisions between these electrons and molecules—and also the forces between the electrons themselves—are negligible, then electric waves are propagated as if the dielectric constant of the medium were reduced by , from which it appears that, so long as the approximations are valid, the velocity of propagation of the waves can be increased indefinitely by increasing either the electron density or the wave-length λ. Several later authors have attempted to take account of the collisions between electrons and molecules, assuming free paths or velocities according to Maxwell's laws for a uniform gas, and it appears that the above law holds only for short waves; but it is doubtful how far the properties of a uniform gas can be assumed when periodic forces are acting. In the first part of this paper an alternative method of solution is given by means of Boltzmann's integral equation for a non-uniform gas, the analysis being similar to that used by Lorentz in discussing the motion of free electrons in a metal. Only the case when ν is small is considered, i.e. the interactions of electrons with one another and with positive ions are neglected. How far it is possible to increase the velocity of propagation by increasing ν is a more difficult question, but it seems possible that the forces between the electrons and ions may impose a limit just as collisions with neutral molecules limit the effect of increasing the wave-length.

In view of the interest now taken in Cremona Transformations in more than three dimensions, some account seems desirable of such transformations in four dimensions. Many of the ideas in two and three dimensions are capable of immediate extension. In this paper attention is directed to the new possibilities in regard to the Principal and Fundamental Systems. The paper is written on the lines and with the notation of Miss Hudson's book.

The word “freedom” is used in this paper with the same meaning as “Konstantenzahl"—the number of free constants—and corresponds very roughly to the term “degrees of freedom” as used in elementary mechanics. “Freedom of a manifold” is used as a convenient abbreviation for “freedom of the class of manifolds of the same specification as the given one”. At the outset the idea is rather vague; in the background there is an intuitive notion of a definite number associated with any given manifold—the number of conditions that manifolds of the same specification can be made to satisfy. This paper is intented to give some precision to this idea, and to formulate rules which will enable the freedom of a given manifold to be calculated.

Experiments on the emission of secondary electrons from hot nickel surfaces bombarded by Cs+ ions at normal incidence show that the emission is a function of bombarding voltage and target temperature. The emission is negligible below 300 volts and increases steadily with further increase of the bombarding voltage, rising to 4% at 4000 volts with the target at 950° C. Increase of temperature causes the secondary emission to diminish. If positive ions are allowed to evaporate from the hot target the number of Cs+ ions leaving the surface may, under certain conditions, be equal (with an accuracy greater than 1%) to the number arriving in the incident beam.

I much appreciate the kindness shown me in many ways by Lord Rutherford. The experiments were commenced at the instigation of Dr M. L. E. Oliphant and I gratefully acknowledge that this paper represents to a great extent the results of his advice and assistance. The work was made possible by a grant from the Department of Scientific and Industrial Research.

In a previous paper the nature of the phenomena occurring when electrons are ejected from metal surfaces by the impact of metastable atoms and positive ions was discussed. It was shown that electrons may be ejected by excited atoms at considerable distances from the surface, and by considering the case of an excited hydrogen atom at the centre of a spherical cavity in the metal the order of magnitude of the effects to be expected and the velocity distribution of the ejected electrons was determined. In this paper the theory will be extended in two directions.